【k个最小不相邻连续子区间】 数据备份

传送门

题意

给定 \(n\) 个位置（距离原点），每个位置上有一个公司，\(k\) 表示可以用的网线数量，
每个网线将连接两个公司且每一个公司只能连接一个网线，求满足 \(k\) 对配对情况下，所有电缆长度的最小值。

数据范围

\(\begin{array}{l}2 \leq n \leq 100000 \\ 1 \leq k \leq \frac{n}{2} \\ 0 \leq s \leq 1000000000\end{array}\)

题解

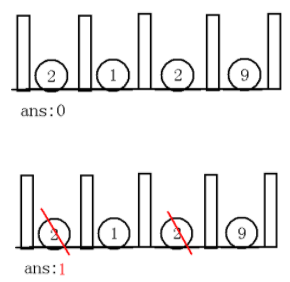
每相邻两个办公楼之间的距离算出来，抽象为线段，也就是有 \(n−1\) 个线段，第 \(i\) 个线段的权表示第 \(i\) 栋楼与第 \(i-1\) 栋楼的距离
每次考虑最小线段

• 最小线段相邻的两个线段要么不选，要么同时选，因为选了最小值就不能选旁边的所以每次选择最小的，
• 然后将最小的两边的和减去最小的加入到集合之中，因为两者相加即除了最小值的两边，这样可以是一个反悔机制

并且当前的当要在最小值外选扩展另一条边的时候 \(d[i-1] + d[i+1] -d[i]\) 正好能表示两条边的时候会增加的值，
将这个加入 \(set\)，不断选最小值并执行当前的操作最后就是最优值，
因为 \(d[0]\) 和 \(d[n+1]\) 有边界的问题所以设置边界为值域内的无穷大，保证永远不会作为选择被选

Code

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for(int i=a;i<n;i++)
#define per(i,a,n) for(int i=n-1;i>=a;i--)
#define fi first 
#define se second 
#define ll long long
#define mp make_pair 
typedef pair<long long,int> pli;
const int N=1e5+10;
int l[N],r[N];
ll d[N];
int n,k;
void remove(int idx){
    r[l[idx]]=r[idx];
    l[r[idx]]=l[idx];
}
int main(){
    set<pli>s;
    scanf("%d%d",&n,&k);
    rep(i,0,n) scanf("%lld",&d[i]);
    per(i,1,n+1) d[i]-=d[i-1];  
    
    d[0]=d[n]=1e12;
    rep(i,1,n+1){
        l[i]=i-1;
        r[i]=i+1;
        s.insert(mp(d[i],i));
    } 

    ll ans=0;
    while(k--){
        auto t=s.begin();
        ll res=t->fi;
        int idx=t->se,left=l[idx],right=r[idx];
        s.erase(t);
        s.erase(mp(d[left],left));
        s.erase(mp(d[right],right));
        remove(left);remove(right);
        ans+=res;
        d[idx]=d[left]+d[right]-d[idx];
        s.insert(mp(d[idx],idx));
    }
    printf("%lld\n",ans);
}