【分形 分治】 分形之城

传送门

题意

初始如图，每扩建一次即将原来的放在右下方，左上方放原来顺时针旋转90度，左边放逆时针旋转90度的，上面放一模一样的然后再首位相接连接起来

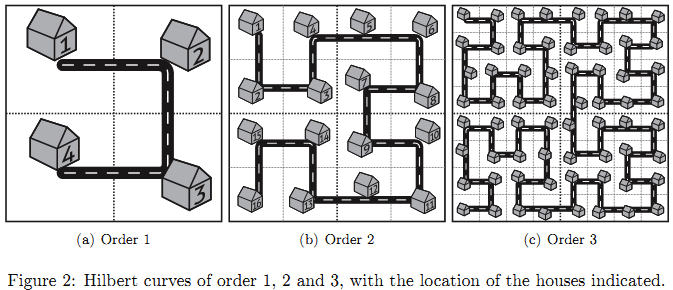
求在任意等级\(N\)城市下，两个编号为\(A,B\)的房屋之间的直线距离,其中每个格子的边长为\(10\)

数据范围

\(\begin{array}{l}1 \leq N \leq 31 \\ 1 \leq A, B \leq 2^{2 N} \\ 1 \leq n \leq 1000\end{array}\)

题解

易知n级城市的房屋个数为\(2^{2n}\)个，\(n\)级由4个\(n-1\)级构成，最开始左边为坐标系原点，为方便后面旋转后取负值，房屋的编号从0开始，横坐标为\(x\)坐标系的点，纵坐标为\(y\)坐标系的点。
从当前等级开始向前找位置然后根据初始坐标递归得到现在的坐标

• 其中当前的房屋编号 \(mod\) 上一级的总房屋数量就是在变换前的房屋编号即\(cnt = 2^{2(n-1)}\)
• 当前编号 \(\div\) 上一级的房屋总数就是在当前的\(4\)块中的那一块
• 通过上一级的左边变换得到当前左边处理的边长是\(len = 2^{n-1}\)

坐标用数组表示，以原点为中心逆时针旋转公式：

• \((x, y) \times\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta\end{array}\right]=(x \cos \theta-y \sin \theta, x \sin \theta+y \cos \theta)\)

以原点为中心顺时针旋转公式：

• \((x, y) \times\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{array}\right]=(x \cos \theta+y \sin \theta,-x \sin \theta+y \cos \theta)\)

\(len\)为格子的边长，房子间的间隔是\(len-1\)

• 处于左上角的城市

  • 顺时针旋转\(90°\) 后\(( x , y ) = ( y , -x )\)，再水平反转为\((y,x)\)

• 处于右上角的城市

  • \(x\)轴不变， \(y\)轴的长度\(+len\)

• 右下角

  • \(x\)轴、\(y\)轴都\(+len\)

• 左下角

  • 因为坐标是从\(0\)开始的，并且除了横纵纵坐标为\(0\)的外全部变了符号

  • 所以逆时针旋转\(90°\)后\(( x , y ) = ( -y , x )\)

  • 再水平翻转后为\(( - y , - x )\)，再移动就是\((2len-1-y,len-1-x)\)

Code

#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=a;i<b;i++)
#define pll pair<long long,long long>
#define fi first
#define se second
#define ll long long

using namespace std;
const int N=1010;

int _;

pll get(ll n,ll no)
{
    if(n==0) return {0,0};
    ll len=(ll)1<<(n-1),cnt=(ll)1<<(2*(n-1));

    pll now=get(n-1,no%cnt);
    ll x=now.fi,y=now.se;
    ll z=no/cnt;
    if(z==0) return {y,x};
    else if(z==1) return {x,y+len};
    else if(z==2) return {x+len,y+len};
    else return {-y+2*len-1, -x+len-1};
}

void solve()
{
    ll n,a,b;
    scanf("%lld%lld%lld",&n,&a,&b);

    auto A=get(n,a-1);
    auto B=get(n,b-1);

    double x=A.fi-B.fi,y=A.se-B.se;
    printf("%.0lf\n",sqrt(x*x+y*y)*10);
}

int main()
{
    cin>>_;
    while(_--) solve();
}