LeetCode 刷题笔记
杂记
-
对于偏数学的问题,可以尝试使用数学解法,诸如
分类讨论等。1131. 绝对值表达式的最大值 -
有关循环的判别 可以使用
快慢指针来甄别,如果快指针追上了慢指针说明存在循环 -
有关链表或者二叉树的 逆转输出,可以采用 后序遍历的方式完成。(PS:一般对于递归先用 temp 变量暂存,之后在后序遍历的过程中,使用暂存变量,完成逆转逻辑)
-
当需要对两条序列进行扫描对比的时候,常用的优化算法是 先扫描较短的那一条序列
-
查找子序列可以使用堆栈的思想
-
使用 sort 排序之前可以思考是否可以通过一次遍历来获取最大的k个值
-
要求正序输出 可以使用栈结构:逆序入栈, 也就等效于正序出栈
-
如果leetcode报类型错误时,很可能是因为自己在IDLE中取消了对于某种类型的注释造成的
-
“之”,“锯齿形”遍历都是具有先入后出的特性(对于孩子节点而言),使用栈来保存当前遍历的节点的孩子节点,(PS: 每一层的输出可以通过调整奇偶层 左右 节点不同的入栈顺序来保证,如果要求从左到右,则先入栈右子节点, 如果要求是从右到左则先入栈左子节点)
-
二维矩阵的斜对角线遍历规则
- 主对角线: $j - i = k$
- 副对角线: $j + i = k$
-
Python的整数除法是向
-∞取整的,诸如 C语言等都是向 0 取整的 -
坑:- 对于大数, 如果直接 float 转换成 int 会发生精度损失,所以在 类型转换的时候需要特别注意。可以使用decimal 实现高精度的浮点计算。
-
两条直线是否平行,可以使用向量积 $absin(\theta)==0$判别
-
计算任何日期是属于星期几:蔡勒公式蔡勒公式_百度百科 (baidu.com)
-
Python 中, a, b = c, d 操作的原理是先暂存元组 (c, d),然后按左右顺序赋值给 a 和 b 。
-
去重 不要 只想着 使用数据结构 集合 来进行, 有许多都是可以在算法层面进行去重的。
-
能通过迭代运算获得的就应该优先使用迭代算法,而不应该是使用递归算法,递归的开销一般比迭代大的多。
-
与循环相关的算法,一定要注意看看是否可以实现剪枝,剪枝可以极大提高效率。18. 四数之和 - 力扣(LeetCode) (leetcode-cn.com)
-
丑数: 定义就是 可以因式分解为 制定质因子的乘积的数,1 是丑数的初始值。
-
对数时间的复杂度 一般 需要 联系到 二分的思路。
-
优先级顺序
![这里写图片描述]()
-
Python 里面 形式 a = b = 3,的赋值过程是先将 3 赋值给 a, 其后将 3 赋值给 b。 这与 JavaScript 存在不同。在赋值给引用变量的时候特别重要。eg :
prev.next = prev = node -
合法括号的生成以及判断问题
- 在生成过程中一定有左括号大于等于右括号的规律存在。
-
Python 负数索引的时候,如下,注意中间的值不能是负数,如果想表示倒置到0,则slice切片中间的值应该赋值为 None
s = '1234' s[3:-1:-1] 是错误的因为中间的-1被认为是最后字符索引了 正确的索引方式是 s[3:None:-1] -
对于有多个控制条件的寻求最优解的通法是,枚举其中一种条件的所有情况,再统计在该条件下的最优解,最后进行比较即可。
-
比较 a 是否是 b 的子序列的暴力解法 -----
使用迭代器,优美def subseq(word): # 判断 word 是否是 S 的子序列 it = iter(S) return all(x in it for x in word) # x如果不与it产出的元素相等,则it会不断产出值进行比较 -
字典结构的使用技巧
a = {1: 3} a.pop(1) # 删除字典中key为 1 的键值对,并且放回对应的值 a.pop(5, None) # 如果a中没有5作为键,则返回第二个参数作为默认值 -
迭代器的一些使用技巧
a = iter(range(3)) next(a, None) # 调用next产生元素,当迭代器产出所有的元素之后,默认会抛出StopIterationError错误,使用第二个参数可以指定所有元素产出之后,产出默认值(不报错) -
元组
- () 代表的是空元组,
-
(1, ) 代表的是只有一个元素的元组,只有一个元素的时候需要使用逗号
-
取整 $ \frac{x}{y}$
- 向上取整---> $\frac{x+(y-1)}{y}$
- 向下取整 ----> $ \frac{x}{y} $
-
对于二维平面的点的几何运算,可以将二维平面看出实轴与虚轴,这样子平面上的二维左标可以由一个虚数
complex进行表示,求两点距离等价于 两个虚数做差再取绝对值,即$dist(P, Q) = abs(P-Q)$ -
对于大数循环明显超时的那种,通常分析可以发现大数循环通常是没必要的,在大数的条件下,答案是定值,可以进行剪枝。
-
数据量特别小的情况,一般都是需要枚举的,考虑枚举的过程可以使用二进制中的状态压缩技巧来实现 -
一般条件下,Leetcode 网站能够接受的最大循环次数为小于等于 $k*10^6$
位运算
异或运算
1.交换律(异或可以交换位置):a ^ b ^ c <=> a ^ c ^ b
2.任何数与0异或为任何数 0 ^ n => n
3.相同的数异或为0: n ^ n => 0
### 重要的点
4 4i⊕(4i+1)⊕(4i+2)⊕(4i+3)=0 # 异或的性质 1^2^3 = 0
5. 对于1...n 进行异或运算有下面性质
k, res = divmod(n, 4)
res = 0 --> n
res = 1 --> 1
res = 2 --> n+1
res = 3 --> 0
6. c = a ^ b 则有 a = c ^ b
7. 对数字的取反也可以使用异或来完成,和指定位数全为 1 的数字进行异或
res ^ 0xffffffff 表示的就是对 res 后32位取反
-
异或运算 可以 用于找出字符串中出现奇数次的那唯一一个单词. 可以用于处理判别回文序列
-
判别两个数字是否是正负不同号的技巧
a ^ b < 0 说明a,b 异号 (最高位符号位不同导致的) a ^ b >= 0 说明a,b 同号 -
可以找寻系列中唯一一个只出现奇数次的数字【字符ascii码同样适用】
-
位运算 是优先级
最低的运算符 -
二进制 源码,反码,补码:这样给小白讲原码、反码、补码,帮她彻底解决困扰了三天的问题 - bigsai - 博客园 (cnblogs.com)
-
python 二进制 不区分 有符号 与 无符号,统一是按无符号处理。
因为「有符号整数类型」(即 int 类型)的第 31 个二进制位(即最高位)是补码意义下的符号位,对应着 $-2^{31}$,而「无符号整数类型」由于没有符号,第 31个二进制位对应着 $2^{31}$ 。所以,对于某些题目,需要对 31 位进行特俗处理,即将python 中的 第 31 位对应的 $2^{31}$ 转换位$-2^{31}$。
-
Python中无具体位数概念,其是无限位的,即负数的符号位是无限个前导1,同理正数也是无数个前导0。在进行模拟位运算的时候,通常截取出后32位进行模拟,最后依据数至是否超过$2^{31}-1$来判断是否是负数,如果是负数需要将后32位取反,最后再对整个结果取反。
将32位的负数补码,返回成python 可以识别的形式 ~ (res ^ 0xffffffff) res ^ 0xffffffff 表示的是对 res 的后 32 位进行取反剑指 Offer 65. 不用加减乘除做加法 - 力扣(LeetCode) (leetcode-cn.com)
# 使用位运算进行模拟加法过程,同时处理含有负数的情况 class Solution: # 位运算 异或 与 或运算 def add(self, a: int, b: int) -> int: x = 0xffffffff a, b = a & x, b & x while b != 0: # a ^ b 表示的是无进位的加法, (a & b) << 1 表示的是进位 a, b = a ^ b, ((a & b) << 1) & x # b 的更新一定要 和 x 进行与运算 return a if a < 0x80000000 else ~(a ^ x) -
lowbit 算法,也就是找寻二进制的最低位为 1的 位置进行处理。
-
直接将
n二进制表示的最低位 1 移除 : n&(n-1) ,得到 最低位 之前的高位数值 -
直接获取
n二进制表示的最低位的 1 的数值。 n&(-n),,利用了负数是正数的补码,即反码 + 1 -
由 6, 7 推导出,判断数字 n 是否是 2 的幂有以下两个方法:
- $n&(n-1) == 0$
- $n&(-n) == n$
- $x & (x−1)$ 可以将 x 的二进制表示中的最低位的 1 置成 0。
- $x&(-x)$可以将 x 的最低位为1的数字表示出来
-
判别两个数的符号是否相通,可以通过二进制中 的符号位是否为1来判断, 正数的符号位为 0 ,负数的符号位为 1, 这就说明 正数 和 负数 进行异或的话,符号位还是为 1,也就是结果还是负数。
-
位掩码 与 位运算 可以对数的二进制任何位置进行操作
逻辑与 &
-
n & (n-1) 可以用来消除最后一个1(n的二进制表示最后一位1)
-
可以找寻一个数字中,由其二进制中任意个1组成的所有可能的数字
n # 求n mask = n ans = [] while n: ans.append(n) n = (n - 1) & mask # 十分巧妙,即每次都是将 n 缩小的与 mask 位中 1 重合的次小数
或运算
或运算,是无进位的加法运算
状态压缩技巧(使用于n较小的时候)
-
(做n个元素的组合,可以使用状态压缩技巧)在给定n个元素的时候,枚举n 个元素的选择状态可以基于二进制的表示即,$2^{m}$ 表示的是选择第 m + 1 个元素。可以实现0(1) 空间复炸度。
-
小写字符串的奇偶性判断
大小写转换使用位运算
1. (--大小写互换--)大写变小写、小写变大写 : 字符 ^= 32;
2. (--全部小写--)大写变小写、小写变小写 : 字符 |= 32;
3. (--全部大写--)小写变大写、大写变大写 : 字符 &= -33;
位运算符 运算的 优先级是 低于 数学运算符的
#### 有关于 2 的 幂函数,都可以通过位运算进行 #### 状态压缩
- 指的是将某个状态是否发生,映射到一个树的bit位上。
bitmap算法
- 对连续数字以32为桶容量进行分组,在每一个组中有一个32位的数字,第 i 位表示的是 第 k 组中的第 i 个元素。举个例子比如整数num其应该落在:$num // 32$ 的桶中,是 第 $num % 32$ 个元素。
- 705. 设计哈希集合 - 力扣(LeetCode) (leetcode-cn.com)
进制转换
可以通过递归来模拟k进制的右移过程
经典例题
格雷码
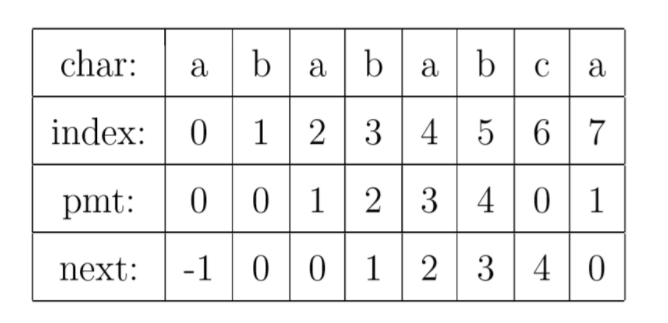
在一组数的编码中,若任意两个相邻的代码只有一位二进制数不同,则称这种编码为格雷码,另外由于最大数与最小数之间也仅一位数不同,即“首尾相连”,因此又称循环码或反射码。
- 递归生成算法
-
循环位运算生成算法
gray = [0]*n for i in range(n): gray[i] = i ^ (i >> 1) # 第 i 位格雷编码
树
特性
- 我们知道在树(甚至图)中,所有节点的入度之和等于出度之和
- 树的修改需要借助 递归 的方式
- 要求树的深度最小,一般需要联想到平衡性,【中点性质】
- 路径和问题可以使用
前缀和/前缀计数表的思想,因为某一段路径就是相当于区间的概念,具有连续性。
主要题型
- 判断是否是子树
- 递归的方法
- 序列化 + KMP模式匹配问题(比较优秀的方法,时间复杂度是线性的)
- 间隔度问题,在一棵树上找寻到某一个节点为定值的那些点的集合(
树转换为图)- 通过DFS 构建无向图的邻接表
- 对构建的图使用 BFS 来收缩间隔度为定值的节点集合
二叉搜索树
-
二叉搜索树的中序遍历得到的是单调递增的序列
-
验证二叉搜索树的前序遍历结果 【使用局部有序特性,单调栈 0(n) 的方法】
class Solution: def verifyPreorder(self, preorder: List[int]) -> bool: stack = [] val = float('-inf') # val记录的是除去遍历节点的子树的最小值 for i in preorder: if i < val: return False # while stack and stack[-1] < i: # 左子树遍历完全,回溯到根节点 val = stack.pop() stack.append(i) return True
完全二叉树
- 根节点在 0 层, 第h层的节点数是 2^h,
- 排列是紧密靠左的,因此对于最大层数为 h 的完全二叉树,节点个数一定在 $[2^h ,2^{h+1} −1]$ 的范围内,可以在该范围内通过
二分查找的方式得到完全二叉树的节点个数。 - 如果 h 层是满节点,那么节点总数是 2^(h+1) - 1
- 对于二叉树每一个节点的路径可以抽象为数字的二进制表示,除了最高位,每一位都可以抽象为节点路径的一次选择,0表示选择左子树,1 表示右子树 ,从次高位到最低位表示的是树从根节点开始选择的路径
树的序列化与反序列化
-
如果对
空节点用特殊符号进行标记的话,则单靠前序,后序都可以进行反序列化还原树,而单靠中序遍历不能完成 -
如果
没有对 空节点进行特殊标记,则需要两种遍历方式搭配使用,即 前+中,后+中,但是 前+后 不可以。 -
如果是二叉搜索树的话,可以使用前 or 后序遍历,再搭配二分查找完成反序列化。或者 二叉树可以通过前序序列或后序序列和中序序列构造(即与2相同)。
-
还原顺序:
- 如果是根据后序遍历得到的结果进行反序列化,需要先还原右子树,其次是左子树
- 如果是根据前序遍历得到的结果进行反序列化,需要先还原左子树,其次是右子树
-
确保树的平衡性
使用的策略主要是找寻给定序列的中点为root节点,左半部分为左子树,右半部分为右子树 即可。
迭代 中序遍历
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
if root is None:
return []
# 隐含栈
stack = []
# 把当前节点的完全左子树路径压入栈
def order(root):
while root is not None:
stack.append(root)
root = root.left
order(root) # 将根节点的完全左子树路径部分压入栈
ans = []
while stack:
top = stack.pop() # 栈顶元素即为 最左端元素 出栈
ans.append(top.val)
order(top.right) # 将当前节点的右子树部分也入栈
return ans
迭代 前序遍历
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
if root==None:
return []
stack=[root]
res=[]
while stack:
s=stack.pop()
res.append(s.val)
# 前序 要求 root left left 所以子节点要求倒序入栈
if s.right:
stack.append(s.right)
if s.left
stack.append(s.left)
return res
迭代 后序遍历
# 由于 前序遍历的顺序 是 root left right
# 而后序遍历的顺序为 left right root,倒转一下就是 root right left
# 恰巧就是 前序遍历中 左右子节点交换位置部分,最后再翻转成原状态即可
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
if root==None:
return []
stack=[root]
res=[]
while stack:
s=stack.pop()
res.append(s.val)
if s.left:#与前序遍历相反
stack.append(s.left)
if s.right:
stack.append(s.right)
return res[::-1] # 翻转回原状态
找寻最大的第k个元素
使用 生成器来 惰性生产值,这样只需要生成k个即可,节约了时间
填充每个节点的下一个右侧节点指针
采用前序遍历的方式,实现dfs逻辑即可
注意: 树的题目,使用DFS解法时,一定要注意迭代方式
高级数据结构
字典树(大多用于字符串中)
-
字典树 又 称为前缀树,是特殊的n叉树解构,需要一个根节点来驱动。
数组中两个数的最大异或值 - 数组中两个数的最大异或值 - 力扣(LeetCode) (leetcode-cn.com)
-
对于数值按照字典序排列实际上不需要构建真的前缀树,只要字节点是 父节点 * 10 + i (i in range(10))的关系, 这就是数值化的前缀树。
-
一道典型的数值二进制字典树问题
# 模板
# 字典树的节点类
class TrieNode:
def __init__(self):
self.children = defaultdict(TrieNode)
# 字典树类,实现了插入,与搜索方法
class Trie:
def __init__(self, nums):
self.root = TrieNode() # 根节点
for n in nums:
self.insert(n)
def insert(self, n): # 从右向左每一位插入Trie
cur = self.root
for i in range(31, -1, -1):
cur = cur.children[(n>>i) & 1] # 创建每一个字节点,并且移动指针到子节点上
def searchMax(self, n):
res, cur = 0, self.root
for i in range(31, -1, -1): # 从右向左找最多xor=1的儿子
bit = (n>>i) & 1
if bit ^ 1 in cur.children: # 找到就向儿子走(第i位的二进制可以满足异或结果为 1)
cur = cur.children[bit ^ 1]
res += (1<<i)
else: # 没找到就向bit走,因为有可能之后会找到xor=1的儿子
cur = cur.children[bit]
return res
class Solution:
def findMaximumXOR(self, nums: List[int]) -> int:
t = Trie(nums)
return max([t.searchMax(n) for n in nums])
线段树SegmentTree
算法:满二叉树
线段树是一种非常灵活的数据结构,它可以用于解决多种范围查询问题,比如在对数时间内从数组中找到最小值、最大值、总和、最大公约数、最小公倍数等。
主要用于处理区间问题
- 区间异或问题代码如下
class NumTree:
def __init__(self, nums):
self.n = n = len(nums)
self.nums = [0]*2*n # 完全二叉树(索引位置为0的空出来)
# 叶子节点赋值
for i in range(n, 2*n):
self.nums[i] ^= nums[i-n]
# 父亲节点赋值
for i in range(n-1, 0, -1):
# 索引关系构建左子树与右子数
self.nums[i] = self.nums[2*i] ^ self.nums[2*i+1]
def update(self, idx, val):
pos = self.n + idx
self.nums[pos] = val
while pos > 0: # 更新是从叶子节点,一直更新回溯到根节点
l = r = pos
if pos % 2: l = pos - 1 # 如果 pos 是右子节点(还差左节点,左节点为 pos - 1)
else: r = pos + 1 # 如果 pos 是左子节点(还差右节点,右节点为 pos + 1)
pos //= 2
self.nums[pos] = self.nums[l] ^ self.nums[r]
def xorange(self, left, right):
l = self.n + left
r = self.n + right
res = 0
while l < r:
if l % 2:
res ^= self.nums[l]
l += 1
if r%2 == 0:
res ^= self.nums[r]
r -= 1
# 回溯到根节点
l //= 2
r //= 2
# 如果回到了同一个根节点
if l == r: res ^= self.nums[l]
return res
区域和检索 - 数组可修改 - 区域和检索 - 数组可修改 - 力扣(LeetCode) (leetcode-cn.com)
树状数组BIT
-
前缀和用于没有单点修改的区间问题
以下是一个在
树中使用前缀和技巧的题目,较为经典 -
树状数组实质是
动态的前缀和,支持高效的单点修改和动态区间问题(求和)lowbit 的妙用
# 以求区间异或问题为例
class BIT:
def __init__(self, nums):
self.n = len(nums)
self.store = [0]*(1+self.n) # 树状数组真实有效的索引从 1 开始
for i in range(1, 1+self.n):
self.update(i, nums[i-1])
# 单点更新
def update(self, idx, val):
while idx <= self.n:
self.store[idx] ^= val
idx += idx & -idx # lowbit 位加1
# 高效查询前缀异或值
def xorrange(self, cur):
res = 0
while cur > 0:
res ^= self.store[cur]
cur -= cur & -cur # 去掉 lowbit 位
return res
并查集
- 并查集实质是用数组来实现树的层次结构
- 因此对于连通量的判断,需要借助变量,每当 union 不同组时, count - 1
- 直接对于 数组 的去重计数,往往大于等于实际 连通量 的数量,因为 并查集里面的 root 节点是存在 层级关系的,所以每个组的父亲节点 并不一定意味着是 根节点
路径压缩技巧:在 find 函数中实现,主要是将某一节点的父亲节点直接直想其爷爷节点平衡化技巧:在 union 的过程中实现,主要指 在合并的时候 要将重量轻的子树插入到 重量重的子树来
class UFoid:
def __init__(self, n):
self.root = list(range(n))
self.weight = [1]*n
def find(self, a):
if a == self.root[a]: return a
tmp = self.root[a]
self.root[a] = self.root[tmp]
return self.find(tmp)
def connect(self, a, b):
return self.find(a) == self.find(b)
def union(self, a, b):
if self.connect(a, b): return
root_a, root_b = self.find(a), self.find(b)
# 由平衡性知道 要将重量轻的 插入到 重量重的子树来
if self.weight[root_a] < self.weight[root_b]:
root_a, root_b = root_b, root_a
self.root[root_b] = root_a
self.weight[root_a] += self.weight[root_b]
堆与队列
堆
- 将元素压入堆中,堆顶元素是在索引为 0 的数组位置
固定容量的堆
方法1: 可以通过固定大小的有序结合来实现
from sortedcontainers import SortedList
a = SortedList()
for i in nums:
a.add((-rec[i], i))
if len(a) == k + 1:
a.pop(-1)
优先队列
- 优先队列 一个 item 可以 存放 多个元素
from queue import PriorityQueue as pq
q = pq()
q.put((priority, 1, 0, 1)) # priorty 之后的元素是 item成员
优先对列是否为空
需要使用 内置方法 empty 判别
-
优先队列或者是堆在删除一个元素的时候,需要
0(N)时间的查询元素,以及O(logN)时间的移除元素。优化是:使用延迟删除策略,使用字典对要删除元素进行计数,当堆顶元素在字典中的时候,字典中待删删除元素次数减一,当次数为0的时候,移除堆顶元素。(这就省略了线性的查询时间)
双端队列
-
基于类的实现
-
基于数组的实现
BFS
BFS 中十分重要的一点,就是必修明确入队列的条件。以及去重
- 在寻求最少花费的时候,一个节点可能会被遍历多次,为了避免一个节点的无线重复遍历,这时候的入队列的条件可以设置为 使得从起点到达该点的费用变少的时候,才入队列
DFS
-
python 中 dfs 可以基于
协程的写法 (十分优雅!!)class Solution: def leafSimilar(self, root1, root2): def dfs(node): if node: if not node.left and not node.right: yield node.val yield from dfs(node.left) yield from dfs(node.right) return list(dfs(root1)) == list(dfs(root2)) -
汉诺塔问题的 递归函数状态 设计的十分巧妙!!!# s 是开始立柱, f 是 辅助立柱, t 是目标柱子 # a 是代表 开始立柱上 需要移动的 盘子数目 # 中序遍历 def dfs(a, s, f, t): if a == 1: t.append(s.pop()) return # 将 a-1 个1盘子,通过 目标柱子,先移动到辅助柱子上 dfs(a-1, s, t, f) # 将开始立柱上最大的盘子移动到目标柱子上 t.append(s.pop()) # 通过 开始柱子将辅助柱子上的 a-1 个盘子移动到目标柱子上 dfs(a-1, f, s, t) dfs(len(A), A, B, C)
回溯问题
-
经典题型 (数据规模一般小于等于20)
-
当数据规模大于等于20/30的时候,单纯的回溯已经面临TLE问题,所以使用折半搜索 + 状态压缩 技巧
折半搜索(meet in the middle):指的就是将数组拆分成两个部分,分别进行回溯 / 状态压缩 枚举,最后使用二分来查找答案
string类型题目
判断括号的有效性
有效的具有括号的字符串有以下特性:
- 字符串中有相同数量的
"("和")"。 - 从左至右遍历字符串,统计当前
"("和")"的数量,永远不会出现")"的数量大于"("的数量
字符表达式的可能运算结果
分治算法,以运算符为切割符进行分治处理。
553. 最优除法 - 力扣(LeetCode) (leetcode-cn.com)
栈
-
计算器运算
将 符号和数字一起 视为一个整体,如果是 +, - 将数字压入栈,如果是乘除则与栈顶元素运算后入栈,最后对栈求和即可。(初始化时,设定符号为 + )
-
逆序处理序列,需要想到利用栈来处理
单调栈
-
单调栈可以用来找寻第一个大于/ 小于 某个元素的索引
-
单调栈用于求一类 next greater number 问题,时间复杂度为 0(N)
-
在接雨水等问题中,需要同时确定左右边界,左边界(小于 nums[i] 的左侧第一个元素索引), 右边界(小于nuns[i]的右侧第一个元素索引),可以使用两个单调栈来维护处理。
# 右边界的确定 stack = [] for i in range(n): more_less[i][0] = nums[i] # 栈顶元素如果大于 nums[i] 也就意味着找到右边界 while stack and nums[stack[-1]] > nums[i]: item = stack.pop() more_less[item][-1] = i stack.append(i) # 还保留在栈中的元素,就是无右边界,设置为n while stack: item = stack.pop() more_less[item][-1] = n # 左边界的确定 stack = [] for i in range(n-1, -1, -1): # 栈顶元素如果大于 nums[i] 也就意味着找到左边界 while stack and nums[stack[-1]] > nums[i]: item = stack.pop() more_less[item][1] = i+1 # 因为浅醉和每一个元素都是左闭右开的,所以左边界要+1 stack.append(i) # 还保留在栈中的元素,就是无左边界,设置为0, presum[0] == 0 while stack: item = stack.pop() more_less[item][1] = 0
经典题目
962. 最大宽度坡 - 力扣(LeetCode) (leetcode-cn.com)
常见题型
-
计算器的 数字 表达实现 题
-
处理子问题的时候,以
"(“作为处理子问题的递归入口标识,对于”)“作为递归的出口标识。726. 原子的数量 - 力扣(LeetCode) (leetcode-cn.com)【任何带有括号的字符串解析,都是利用递归来处理】
-
链表
-
环形链表
其处理的过程包括两步骤:
- 使用快慢指针(1步,2步间隔)找到相交点
- 从相交节点 以及 头节点同时出发,遇见的第一个节点就是环的起始点
-
找交点问题
- 多链表的相交问题,是从两条链表的头节点同时出发,到达链表的末尾的时候,就切换到另外一条链表继续前进。相遇的点就是交点,或者是None。因为在 m + n 步之后一定会停止即(两个指针同时指向了 None)。PS:m,n 是两条链表的长度。160. 相交链表 - 力扣(LeetCode) (leetcode-cn.com)
-
主要技巧
- 链表拆分(空间复杂度位 0(1),因为在原链表的修改不视为空间的使用) 复制带随机指针的链表 - 复制带随机指针的链表 - 力扣(LeetCode) (leetcode-cn.com)
- 虚拟头节点
- 快慢指针(检测循环)
排序
归并排序
-
归并排序的base-case:
- 分解后只有一个元素的情况,注意如果是链表等还需要将该节点next指针指向 None
- 分解后没有元素的情况
- 最适合
链表的排序算法是归并排序
Top K 问题
- 使用排序算法之后,在获取前 k 位
- 使用优先队列(堆排序),确保插入的有序性
最大不重复子区间/时间调度/射气球问题
- 都是利用贪心算法, 并且基于 区间右边界进行排序处理
数组重排序组合成最小的数
-
主要是需要知道 a, b 两个数字,在组合时,谁排前面先组合。
有以下规则:假设 a,b 都是字符串
a + b < b + a 说明 a 在b 前面, b 在 a 后面结合
查看值是否落入某个定长的范围内的时候,使用桶排序
基数排序
只能处理正数数据
-
基数排序是一种不基于比较的排序算法,时间复杂度为 0(n)基数排序_百度百科 (baidu.com)
import math def sort(a, radix=10): """a为整数列表, radix为基数""" # 这里的 + 1 十分关键 K = math.ceil(math.log(max(a), radix)) + 1 # 用K位数可表示任意整数, 注意需要加 1,因为是实际中 数字的长度, == len(str(max(a))) bucket = [[] for i in range(radix)] # 不能用 [[]]*radix for i in range(1, K+1): # K次循环 for val in a: # 个位数 -> 十位数 ->...不断入桶再合并的过程 bucket[val%(radix**i)//(radix**(i-1))].append(val) # 析取整数第K位数字 (从低到高) del a[:] for each in bucket: a.extend(each) # 桶合并 bucket = [[] for i in range(radix)]更优的实现方式
- 多关键字排序,按个位十位百位依次排序
- 分配一个0到9的桶count数组,从个位排起,对个位取余,按0到9放进对应编号的桶里;
- 使用计数数组,从 0-9 记录累计当前桶的大小
- 对桶的序号进行累加运算,得到桶里最后一个值的下标,然后
从后往前遍历原数组arr,把arr[n]赋值给暂存数组
class Solution: # 基数排序 def sortArray(self, nums: List[int]) -> List[int]: n = len(nums) item = 0 for i in range(n): nums[i] += 50000 # 将负数转换为正数 item = max(item, nums[i]) res = nums.copy() # 主要是记录从个位,十位,百位的变化过程,减少运算 while item: count = [0]*10 for i in range(n): count[res[i] % 10] += 1 count = list(accumulate(count)) # 桶的累计大小 tmp, res2 = [0]*n, [0]*n for i in range(n-1, -1, -1): # 倒序很关键 count[res[i] % 10] -= 1 idx = count[res[i] % 10] tmp[idx] = nums[i] res2[idx] = res[i] // 10 item //= 10 nums, res = tmp, res2 return [i-50000 for i in nums]
桶排序 / 计数排序
- 桶排序也是一种不是基于比较的算法,时间复杂度为 0(N),重点是需要设置合理的桶大小
- 计数排序,是桶大小为1的时候的特殊桶排序
快速排序
class Solution:
# 快排 左闭右闭区间
def sortArray(self, nums: List[int]) -> List[int]:
random.shuffle(nums) # 必须的操作
n = len(nums)
def quick(left, right):
if left >= right: return
l, r, target = left+1, right, nums[left]
while l <= r:
while l <= r and nums[l] < target: l += 1
while l <= r and nums[r] > target: r -= 1
if l > r: break
nums[l], nums[r] = nums[r], nums[l]
l, r = l + 1, r - 1
# 与 r 进行交换是因为 r 最小的时候为 left 即不会越界
nums[left], nums[r] = nums[r], target
quick(left, r-1) # 确定了 nums[left] 的位置在 r 处
quick(l, right)
quick(0, n-1)
return nums
归并排序
归并排序 实质是 后序遍历 的过程
class Solution:
# 归并排序
def sortArray(self, nums: List[int]) -> List[int]:
n = len(nums)
tmp = nums.copy() # 暂存数组
def merge_sort(left, right): # 闭区间
if left >= right: return
mid = (left + right) >> 1
merge_sort(left, mid)
merge_sort(mid+1, right)
p1, p2 = left, mid + 1
cur = left
while p1 <= mid and p2 <= right:
if tmp[p1] <= tmp[p2]:
nums[cur] = tmp[p1]
p1 += 1
else:
nums[cur] = tmp[p2]
p2 += 1
cur += 1
if p1 <= mid: nums[cur: cur+mid-p1+1] = tmp[p1: mid+1]
elif p2 <= right: nums[cur: cur+right-p2+1] = tmp[p2: right+1]
# 同步一下
tmp[left: right+1] = nums[left: right+1]
merge_sort(0, n-1)
return nums
二分查找
1. 常见的有基于 索引 的二分查找
2. 基于 值 的二分查找也是十分重要的
3. 二分查找不一定应用在有序数组中,由于某些局部特性,也可以使用二分查找
162. 寻找峰值 - 力扣(LeetCode) (leetcode-cn.com)
二分变种
一般来说,我们去找一个可行区域的上界,我们用(l+r+1)/2,可行区域的下界用( l+ r)/2,这个需要结合对应的l,r更新规则来理解
以下讨论了解区间何是固定左边界/右边界的条件情况
以下代码都是剑指 Offer II 069. 山峰数组的顶部的正确题解
class Solution:
# 二分
def peakIndexInMountainArray(self, arr: List[int]) -> int:
n = len(arr)
l, r = 0, n - 1
while l < r:
mid = l + (r - l + 1) // 2 # 找寻上界,所以向上取整
if arr[mid] > arr[mid - 1]: l = mid # 在山峰的左侧,要找的是可行区域的上界界
else:r = mid - 1
return r
# mid 本身具有向下取整的特性,所以要避免死循环主要通过固定右边界,不断收缩左边界
class Solution:
# 二分
def peakIndexInMountainArray(self, arr: List[int]) -> int:
n = len(arr)
l, r = 0, n - 1
while l < r:
mid = l + (r - l) // 2 # 在山峰的右侧,所以找的是可行区域的下界
if arr[mid] > arr[mid + 1]: r = mid
else:l = mid + 1
return r
分治算法
- 主要题型
- 表达式的优先生成问题
- 逆序对问题
- 实质是后序遍历算法
- 构造题:932. 漂亮数组 - 力扣(LeetCode) (leetcode-cn.com)
滑动窗口
-
在使用滑动窗口技巧的时候,有时没必要保持窗口元素的有序性的时候,可以使用队列即【普通列表】进行存储。
-
在有些题目里面,保持窗口元素的有序性是十分有必要的,可以使用【有序列表】数据结构,甚至可以搭配二分搜索来使用,降低时间复杂度。220. 存在重复元素 III
# 导入 有序列表 数据结构 from sortedcontainers import SortedList class Solution: def containsNearbyAlmostDuplicate(self, nums: List[int], k: int, t: int) -> bool: # O(N logk) window = SortedList() for i in range(len(nums)): # len(window) == k if i > k: # 窗口滚动 window.remove(nums[i - 1 - k]) window.add(nums[i]) # 保证插入有序 # 找寻 小于 nums[i] 的最大索引值 idx = bisect.bisect_left(window, nums[i]) if idx > 0 and abs(window[idx] - window[idx-1]) <= t: return True if idx < len(window) - 1 and abs(window[idx+1] - window[idx]) <= t: return True return False -
滑动窗口中的最 大/小 值等问题,推荐可以使用 单调队列结构来实现,或者是使用窗口有序集合来实现。
-
滑动窗口需要二义性的条件,在某些字符串类型的题目中,可能需要增加条件来使得二义性的要求得到满足。(所谓的二义性就是滑动窗口的左/右指针在移动的时候,结果是存在明确相反的。)
-
滑动窗口 不一定只是维护一个解的区间,同样的也可以维护区间长度,(注意此时滑动区间不一定是可行解,但是区间长度是最优解)
并查集
-
图问题
-
连通性问题
-
交换元素问题【1722】
比如 [1, 2], [0,1] 则意味着 0,1,2可以任意交换位置,其实质也就是同一个连通量
-
一边查询一边修改结点指向是并查集的特色
-
带权值的并查集(有参考意义) -
字典并查集
求最长连续数字序列长度,实际上也就是求一个连通分量的大小
图
1无向图:.
- 并查集 十分重要
- 可以借助并查集 来 判断是否有环的存在
有向图:
-
邻接表的构建 + 路径记录
-
环路的判断
* (`拓扑排序`:借助出/入度)使用BFS时需要借助 ==节点的出度 或者 入度==,将 入度为 0 的 节点作为搜索的第一步入队列,之后要维护节点的 入/ 出 度 的变换, 将入度为 0 的节点作为搜索的第二部入队列
* 使用 DFS 是要 使用 ==状态记录表 区分 本次 DFS 搜索走过的路径==,用来判断是否有环路,用其它的符号标记不会产生环路的节点,来剪枝。
最短路径问题
主要有以下三种解决方法:
-
Floyd 算法
其原始的三维状态定义为 $f[i][j][k],f[i][j][k]$ 代表从点 i 到点 j,且经过的所有点编号不会超过 k(即可使用点编号范围为 [1, k])的最短路径。
1462. 课程表 IV - 力扣(LeetCode) (leetcode-cn.com)
# dp[i][j] 表示的是 i 是否是 j 发先修课程 dp = [[False]*numCourses for i in range(numCourses)] for i, j in prerequisites: dp[i][j] = True # floyd : 表示从i到j,只经过 0-mid 这些中间点的最小值 for mid in range(0, numCourses): # 首先遍历分割的中间点 for x in range(0, numCourses): # 其次遍历起始点 for y in range(0, numCourses): #最后遍历终止点 dp[x][y] = dp[x][y] or (dp[x][mid] and dp[mid][y]) -
Bellman Ford算法
其原始的状态定义为 $f[i][k]$ 代表从起点到 i 点,且经过最多 k 条边的最短路径
-
Dijistra算法(花费代价必须是正数)基于优先队列的解法
note:前两种实质是动态规划的解法
整数相关
整除运算
- 在python中 整除 分为
浮点数整除 与 整数整除两种。在大树的条件下,这两类得到的结果是可能存在差异的。
# 注意
base1, base2 = 1e9+7, 1000000007 # base1 是浮点数
# 假定的大数
num = 1221312341234324523
num % base2 = 685138199 # 返回整型
num % base1 = 685138156.0 # 返回浮点型
结果是不一致的
坑: 在整除运算的时候,一定要确保 做的是 整数整除,因为 float在大数运算的时候,精度会下降。
不使用乘法运算,来实现乘法 / 快速乘法 / 倍增乘法
# 快速乘法模板
def mul(a, b):
ans = 0
# 使用的二进制位运算来实现乘法
while b:
if b & 1:
ans += a
a <<= 1 # 每次叠加 2 倍
b >>= 1
return ans
不使用 + 实现的加法
class Solution:
# 位运算
def add(self, a: int, b: int) -> int:
a, b = a & 0xffffffff, b & 0xffffffff
while b:
a, b = a ^ b, ((a & b) << 1) & 0xffffffff
return a if a < 1 << 31 else ~(a ^ 0xffffffff)
快速幂运算
- 递归思路,空间消耗 0(logN)
思路:使用递归,每次将问题规模缩小一半,时复是O(logN)
递推关系式:
$$
a^b=\left{
\begin{aligned}
& a*a^{b-1} & b为奇数 \
& (a{\frac{b}2}) & b为偶数\
\end{aligned}
\right.
$$
代码:
# 优雅的递归写法
# 只考虑正数,负数次幂就是 取倒数的关系
def myPow( x: float, n: int) -> float:
def quickPow(x, n):
if n == 0: return 1
if n & 1: # 奇数情况
return x * quickPow(x, n-1)
else: # 偶数情况
return quickPow(x, n // 2) ** 2
return quickPow(x, n) if n >= 0 else 1 / quickPow(x, -n)
- 迭代思路
求 x 的 n 次方, 主要思路就是:
将 n 用 2 进制表示,对于 2进制中1 i 位为 1 的 其对最后结果的贡献是 x**(2**i),
代码:
# 只考虑正数,负数次幂就是 取倒数的关系
def myPow( x: float, n: int) -> float:
def quickPow(x, n):
res = 1
while n:
if n & 1:
res *= x
x *= x # 每次 x 翻一番
n >>= 1
return res
return quickPow(x, n) if n >= 0 else 1 / quikPow(x, -n)
参考资料:50. Pow(x, n) - 力扣(LeetCode) (leetcode-cn.com)
矩阵快速幂算法
应用:矩阵快速幂用于求解一般性问题:给定大小为 n * n 的矩阵 M*,求答案矩阵 $M^{k}$,通常需要并对答案矩阵中的每位元素对 p 取模。
只不过是将快速幂运算运用到矩阵中
时间消耗: O(logn) 的复杂度
base = 10**9 + 7
def matrix_mul(a, b): # 矩阵乘法 a * b
m, tmp, n = len(a), len(a[0]), len(b)
res = [[0]*n for i in range(m)]
for i in range(m):
for j in range(n):
for k in range(tmp):
res[i][j] += a[i][k] * b[k][j]
res[i][j] %= base # 求余
return res
# 矩阵快速幂
def quick_mat_power(mat, n):
ans = [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
while n:
if n & 1: ans = matrix_mul(ans, mat)
mat = matrix_mul(mat, mat) # 矩阵翻一番
n >>= 1 # 右移一位
return ans
1137. 第 N 个泰波那契数 - 力扣(LeetCode) (leetcode-cn.com)
1. 获得某一个整数各个位数上的值
x = 13211234
ans = []
while x:
ans.append(x%10)
x /= 10 # 进位
素数
素数删表法
找寻的是小于等于 n 的所有素数
# 素数删表法
def prime(n):
for i in range(2, int(n**.5)+1):
if n % i:
return False
return True
def prime_table(n):
ans = [True]*(n+1)
for x in range(2, int(n**.5+1)): # 只需要扫描到 sqrt(n) 即可
if prime(x):
for j in range(x**2, n, x): # 优化手段一, 从 x**2 开始,可以避免重复遍历
ans[x] = False # 素数的倍数,不是素数
# 返回素数的个数
return sum(ans[2:])
朴素素数判断
-
6步进素数判别法
6步进素数判别法是基于以下事实,即
大于6的素数一定分布在6的倍数的左右。我们可以把大于等于6的自然数写成6x, 6x+1, 6x+2, 6x+3, 6x+4, 6x+5的形式,其中6x,6x+2,6x+3,6x+4肯定不是素数,所以
素数要么表示成6x+1, 要么是6x+5, 所以是分布在6的倍数的左右的。
进制相关
十进制--->二进制
- 十进制的小数转换为二进制小数,主要是利用小数部分乘2后,取整数部分,直至小数点后为0
数组
-
差分法
差分数组
- 数据取值范围比较小的时候,使用差分数组即可
主要处理 : 上车下车,上飞机下飞机等,在区间某一个特定时间里人数最多的一类问题
例子: 人口最多的年份 - 人口最多的年份 - 力扣(LeetCode) (leetcode-cn.com)
# 差分数组法 def maximumPopulation(self, logs: List[List[int]]) -> int: delta = [0]*101 # 差分数组 offset = 1950 for i, j in logs: delta[i-offset] += 1 delta[j-offset] -= 1 # 死亡年份 - 1 ans = 0 count = 0 mx = 0 for i in range(101): count += delta[i] # 在某个时间的人数,是之前还留在系统的人数之和 if count > mx: mx = count ans = i + offset差分字典
-
数据范围比较大的时候,就不应该使用数组结构了,而是应该使用
差分字典,所谓的差分字典其实也就是OrderedDIct来保存 时序 / 区间 特性,之后于差分数组一致的处理模式。
-
循环数组问题
- 要懂得使用负数索引 以及 (1+i)%n,两个规律
-
树状数组
-
原地顺时针旋转矩阵
解法: step1: 水平翻转上下行,
step2: 根据主对角线进行翻转
主要就是完成了 $matrix[col][n-1-row] = matrix[row][col]$的原地交换算法
-
股票购买问题
$dp[i][j]$ 表示的是 在第 i 天 手上股票的状态为 j 的情况下,能获得的最大利益。
j=1: 表示 手上 持有股票
j = 0: 表示手上未持有股票
-
求数组的众数问题
摩尔投票法
229. 求众数 II - 力扣(LeetCode) (leetcode-cn.com)
每次从序列里选择两个不相同的数字删除掉(或称为“抵消”),最后剩下一个数字或几个相同的数字,就是出现次数大于总数一半的那个。 -
滑动窗口
-
滑动窗口在进行迭代之前的时候,需要利用数组前 size 个元素先构建一个滑动窗口。在迭代的时候只要弹出最早进入滑窗的元素,然后令下一个元素进入滑窗的逻辑即可。
# 解法 2: 滑动窗口 def maxSatisfied(self, customers, grumpy, minutes: int) -> int: total = sum(i*(1-j) for i,j in zip(customers, grumpy)) # 原本就满意的人数 windows = sum(i*j for i,j in zip(customers[:minutes], grumpy[:minutes])) # 窗口状态, 窗口大小为 minutes ans = windows for i in range(minutes, len(customers)): windows += customers[i]*grumpy[i] - customers[i-minutes]*grumpy[i-minutes] ans = max(ans, windows) return ans + total
-
-
子数组问题
主要解法
- 动态规划
-
滑动窗口
-
与target最接近的数组元素和
最接近的三数之和 - 最接近的三数之和 - 力扣(LeetCode) (leetcode-cn.com)
使用的方法是:排序 + 双指针, 双指针有点类似 接雨水 问题。充分利用有序的特性。
-
前缀和 [presum[0] = 0]+ 前缀和计数表[presum = {0: 1} ]
-
顺时针旋转矩阵 90 度- step1: 水平上下翻转
- step2:主对角线翻转
-
顺时针按层填充的数组,大多需要按层来分解求解
-
约瑟夫环问题(存在数学递归解法)
参考资料:Java解决约瑟夫环问题,告诉你为什么模拟会超时! - 圆圈中最后剩下的数字 - 力扣(LeetCode) (leetcode-cn.com)
# 数学解法 递归写法
def lastRemaining(self, n: int, m: int) -> int:
# 后序遍历
# 定义: 在数组长度为n的时候,删除第 m 个元素的时候,最后保留下来的序列号
def dfs(n, m):
if n == 1: return 0
last = dfs(n-1, m)
return (last + m) % n
return dfs(n, m)
# 自低向上的迭代解法
def lastRemaining(self, n: int, m: int) -> int:
res = 0
for i in range(2, n+1): # 枚举的是数组长度
res = (res + m) % i
return res
- 旋转数组特性 首尾相连,
动态规划
知识点
-
动态规划,最重要的点就是
子问题的独立性,只要能剥离出独立的子问题都可以使用动态规划来完成 -
字符串问题有较多可以使用动态规划的技巧
-
积木问题
-
对于转移关系是明确的线性关系的时候,可以使用
转移矩阵和矩阵快速幂算法将时间复杂度下降为对数级别
一维DP
-
一般
子序列问题, 大多都是需要动态规划思想来解决-
最长递增子序列问题 LIS问题
具有0(nlogn) 的解法,需要记住。比较通用
二分查找大于等于 value 的最左侧元素,表示构成 相应的长度的最小元素值更新为 value
class Solution: # O(nlogn) 解法 def lengthOfLIS(self, nums: List[int]) -> int: n = len(nums) # res 是有序的(严格递增的) res = [] # res[i] 表示的是 递增子序列 长度 为 i+1 时,其最小结尾元素 for item in nums: if not res or res[-1] < item: res.append(item) continue l, r = 0, len(res) - 1 # 找寻的是 res 中大于等于 item 的第一个元素 while l <= r: mid = (l + r) // 2 if res[mid] >= item: r = mid - 1 else: l = mid + 1 # 改变相应的值 res[l] = item return len(res)
-
-
打家劫舍系列问题:
状态定义:
-
如果你不偷取当前家庭,那么你得到就是前一个 i - 1 家庭的位置的最优结果。
-
如果你觉得偷取当前家庭,那么你就会得到 i - 2位置的那个最优结果加上当前位置的金额。
-
-
最大整除数组(与1类似,但是需要给出具体的最大集合,值得学习)【宫水三叶の相信科学系列】详解为何能转换为序列 DP 问题 - 最大整除子集 - 力扣(LeetCode) (leetcode-cn.com)
-
思维不要局限在 动态规划 只能基于数组的思维方式,也是可以基于字典等其它复杂结构。
-
最大子数组和问题
- Kadane算法:基于动态规划,状态定义 dp[i] 为以 i 为结尾的最大子树组和
-
常见的状态定义:
定义: dp[i] 表示的是 子树组中 [0...i-1] 范围内符合题意的最值
博弈问题
状态设计的时候,只能从当前选手角度出发进行设计。
-
拿石子只能从数组左边界或者右边界拿,这就保证了区间的连续性,可以使用区间DP来处理。
状态定义:$dp[i][j]$ 表示当剩下的石子堆为下标 i 到下标 j 时,即在下标范围 i, j 中,
当前玩家与另一个玩家的博弈之差的最大值,注意当前玩家不一定是先手。 -
拿到一定数额的选手获胜
通过枚举来实现:状态压缩技巧 + DFS
-
除数博弈问题
dp[i] 表示当黑板写的是 i 的时候当前人员是否必赢
二维DP
-
背包问题 / 排列组合问题 / 完全背包问题
-
背包问题特性:在一定条件下,选择集合的最优子集过程
-
不考虑顺序 背包问题
$dp[i][j]$ 表示的是 使用前 i 个物品,在背包容量为 j 的时候 能获得 的 最大 价值 $dp[i][j]$, 状态转移为 $dp[i][j] = max(dp[i-1][j], dp[i-1][j-nums[i-1]] + nums[i-1])$,分别代表的是 不取物品 nums[i-1] ,以及取物品nums[i-1]。
做选择的时候,第 i 件物品有两种可能,加入背包或者 不加入背包(在这两种状态中选择最优的即可)。
0-1背包问题:416. 分割等和子集 - 力扣(LeetCode) (leetcode-cn.com)
多个限制因素的0-1背包问题:474. 一和零 - 力扣(LeetCode) (leetcode-cn.com)
完全背包问题:518. 零钱兑换 II - 力扣(LeetCode) (leetcode-cn.com)
-
考虑顺序 组合问题---> 排列问题
由于是排列数,所以只需要考虑最后一个元素结合的情况,进而设计转态转移的过程
-
-
最长回文子串
属于单序列2维DP问题
486. 预测赢家 - 力扣(LeetCode) (leetcode-cn.com)
5. 最长回文子串 - 力扣(LeetCode) (leetcode-cn.com)
属于多序列2维DP问题
-
最长公共子序列问题 LCS问题
$dp[i][j]$ 表示的是 str1[ 0 : i ] 和 str2[ 0 : j ] 构成的最大公共子序列长度
当两个序列其中一个数组元素各不相同时,最长公共子序列问题(LCS)可以转换为最长上升子序列问题(LIS)进行求解
-
最长递增子序列问题 LIS问题
-
判断子序列 s 是否存在于 t 中
dp[i][j] 表示字符串 t 中从位置 i 开始往后直到字符 j 第一次出现的位置
base-case: dp[len(t)][*] = m 表示不存在
-
判别是否是子序列的动态规划方法(有点类似next数组的意思)
十分巧妙!$dp[i][j]$ 表示的是 $string[i...]$ 中首次出现 字符 j 转态的 索引位置
树型DP
主要指的是动态规划的转过程是在树型结构上完成的,自底向上,根据左右节点的dp表推导出当前节点的dp表,本质就是后序遍历+动态规划的思想
LCP 34. 二叉树染色 - 力扣(LeetCode) (leetcode-cn.com)
数位DP
- 二进制上的DP
600. 不含连续1的非负整数 - 力扣(LeetCode) (leetcode-cn.com)
区间DP
1039. 多边形三角剖分的最低得分 - 力扣(LeetCode) (leetcode-cn.com)
高维DP
1. 最大矩形
主要题型是寻找二维矩阵中满足一定条件的最大子矩阵问题
1139. 最大的以 1 为边界的正方形 - 力扣(LeetCode) (leetcode-cn.com)
数据规模大---DP技巧
-
缩减数据规模技巧,注意要求的精度在指定范围内,则在超过阈值之后可以用极限表示
-
通过做差,消除递归表达式中的内循环部分,得到新的状态转移方程
经典DP
- DP问题一般都是求最值问题,且
具有最优子结构
5861. 出租车的最大盈利 - 力扣(LeetCode) (leetcode-cn.com)
字符串
KMP算法
-
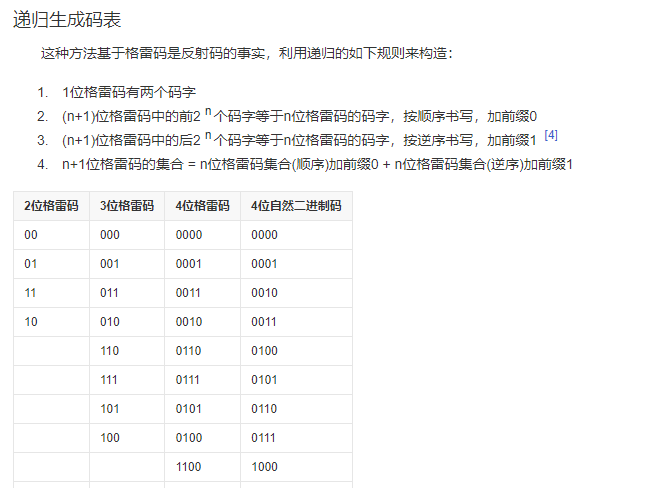
PMT 数组:PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度
-
字符串前缀 与 字符串后缀集合概念
例如,”Harry”的前缀包括{”H”, ”Ha”, ”Har”, ”Harr”}
例如,”Potter”的后缀包括{”otter”, ”tter”, ”ter”, ”er”, ”r”}
要注意的是,字符串本身并不是自己的后缀或者前缀
-
next数组: 将PMT数组向后偏移一位。在把PMT进行向右偏移时,第0位的值,我们将其设成了-1,这只是为了编程的方便。
-
KMP算法高效的一个原因是永远不回退 主字符串指针。
![image-20210710232917307]()
-
接口形式 【需要注意 i,j 初始化的值】
def KMP(main, patten):
m, n = len(main), len(patten)
if not n: return 0
next = getNext(patten) # next 数组
i, j = 0, 0
while i < m and j < n:
if j == -1 or main[i] == patten[j]:
i += 1
j += 1
else: # 回退模式串指针
j = next[j]
# 匹配的字符串区间是[i-j, i-1]
if j == n:
return i - j
return -1
-
高效 求解 next 数组 【需要注意 i, j 初始化的值】
求next数组的过程完全可以看成字符串匹配的过程,即以模式字符串为
主字符串(以 nums[i]为结尾的后缀),以模式字符串的前缀为目标字符串(以nums[j] 为前缀结尾的前缀),一旦字符串匹配成功,那么当前的next值就是匹配成功的字符串的长度。注意:next 默认有下面情况成立:next[0] = -1, next[1] = PMT[0] = 0
所以在更新 next 的时候,直接 主字符串的 i 索引从 1 开始更新,对应的next从 i+1 处更新,因为 next 是 PMT 右移一位的结果。
为何从1开始是因为,字符串要存在后缀集合起码需要 2 个元素。def getNext(patten): n = len(patten) next = [-1] * n # base case next[0] = -1 # next[1] = 0 # 则是循环触发的第一步 # i与j初始相差1,是因为主字符串表示的是后缀,目标字符串表示的是前缀,他们之间起码差 1 i, j = 0, -1 # 主字符串的指针i, 模式字符串的指针 j while i < n - 1: # 以nums[i] 为结尾的 子串的 PMT值 if j == -1 or patten[i] == patten[j]: i += 1 j += 1 next[i] = j else: # 不匹配的话.回退模式串的指针 j = next[j] return next
参考资料:如何更好地理解和掌握 KMP 算法? - 知乎 (zhihu.com)
细节
- split()的时候,多个空格当成一个空格;split(' ')的时候,多个空格都要分割,每个空格分割出来空。
特定字符的重复子串检验
-
如果使用字符串比较的方法,太耗时。一般采取hash策略,即将某一子串 进行 独有编码为一个数字进行比较,则可以在 O(1) 的时间复杂度下,完成重复子串的检验工作。
-
两种方法:将字符串转换成数值进行比较,可以在O(1)的时间复杂度内完成比较
-
Rabin-Karp:使用旋转哈希实现常数时间窗口切片 -
二进制掩码
-
回文子串
回文子串的判断可以使用动态规划预处理,达到0(1) 的时间复杂度
字符串的状态压缩
将字符串转换成数值进行比较,可以在O(1)的时间复杂度内完成比较
-
Rabin-Karp:使用旋转哈希实现常数时间窗口切片 -
二进制掩码
数学
- 三角形求面积公式:

-
求二维任意多边形面积---鞋带公式
![image-20210924192614279]()
数论
-
整除相关:
-
同余定理
如果两个整数 a, b 满足 (a-b)%K == 0,那么有 a%K == b%K。
-
求余的分配定律
$(a*b)\ %\ k = (a\ %\ k)\ (b\ %\ k)\ % \ k$
-
费马小定理
假如p是质数,且a 与 p 互质,即 gcd(a,p)=1,那么a(p−1)≡1(mod p)。
-
判断数字是否能被11整除
奇数位数字之和 - 偶数位数字之和能被 11 整除,则该整数能被 11 整除。即偶数长度的回文数字都不是素数,如1001,1111等
-
-
组合数学
-
把 n 个小球放到 m 个盒子里,盒子不能为空的分法,就是 C(n - 1, m - 1)
-
把 n 个小球放到 m 个盒子里,盒子可以为空,答案为 C(n + m - 1, m - 1)。
-
-
求最大公约数的两种方法
-
辗转相除法
定理: 两个正整数 a 和 b (a > b) ,他们的最大公约数等于 a 除以 b 的余数 c 和 b 之间的最大公约数。 -
更相减损术
定理:两个正整数 a 和 b (a > b),它们的最大公约数等于 a - b 的差值 c 和较小数 b 的最大公约数。 -
优化算法
[漫画算法:辗转相除法是什么鬼? - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/31824895#:~:text=辗转相除法, 又名欧几里得算法(Euclidean algorithm),目的是求出两个正整数的最大公约数。 它是已知最古老的算法,,其可追溯至公元前300年前。 这条算法基于一个定理: 两个正整数a和b(a>b),它们的最大公约数等于a除以b的余数c和b之间的最大公约数。 比如10和25,25除以10商2余5%2C那么10和25的最大公约数,等同于10和5的最大公约数。)
-
-
费马平方和定理
定理:一个非负整数 c 如果能够表示为两个整数的平方和,当且仅当 c 的所有形如 $ 4*k + 3 $ 的质因子的幂均为偶数。 (后半句指的是 c 的质因子分解式中,所有形如 $ 4*k + 3 $ 的质因子都是偶数次的) -
质数分解算法
ans = []
d = 2 # 最小素数
while n > 1:
while n % d == 0:
ans.append(d)
n /= d # 分解出素数 d
d += 1
-
裴蜀定理(贝祖定理)
定理:对于任何整数 $ a, b $ 和他们的最大公约数 $d$ ,关于未知数 $ x,y$ 的线性不定方程(称为裴蜀等式);若 $a, b$ 是整数,且 gcd(a, b) = d,那么对于任意的整数 x,y, ax + by 都一定是 d 的倍数,特别地,一定存在整数 x, y , 使得 ax + by = d 成立。变样表达:ax+by=z 求二元一次方程的整数解(x, y, z 已知,求 a, b 的整数解) 有整数解的前提是 x 与 y 的最大公约数 能被 z 整除 -
康托尔对角线法进行构造不同字符串
原理:构造的子串的第 i 个字符与 第 i 个字符串的第 i 个字符不同,即可确保构造出来的字符串是不在已知集合中的新字符串。
-
对于大于等于1的两个数 a,b 来说,始终存在着 $a * b >= a + b$ 的关系。
随机化算法
Fisher-Yates 洗牌算法 (公平的随机排列)
特点:
- 数据完全加载进数组中
算法
Fisher-Yates 洗牌算法跟暴力算法很像。在每次迭代中,生成一个范围在当前下标到数组末尾元素下标之间的随机整数。接下来,将当前元素和随机选出的下标所指的元素互相交换 - 这一步模拟了每次从 “帽子” 里面摸一个元素的过程,其中选取下标范围的依据在于每个被摸出的元素都不可能再被摸出来了。此外还有一个需要注意的细节,当前元素是可以和它本身互相交换的 - 否则生成最后的排列组合的概率就不对了。打乱数组 - 打乱数组 - 力扣(LeetCode) (leetcode-cn.com)
蓄水池抽样算法
特点:
- 数据量大小未知
- 每个被抽取的概率是相等的
当内存无法加载全部数据时,如何从包含未知大小的数据流中随机选取m个数据,并且要保证每个数据被抽取到的概率相等.
算法:
-
如果接收的数据量小于等于m,则依次放入蓄水池。(蓄水池长度为 m 的数组)
-
当接收到第 i 个数据时,i > m,在 [1, i] 范围内取随机数 d,若 d 落在[1, m] 范围内,则用接收到的第 i 个数据替换蓄水池中的第 d 个数据(索引为 d - 1)。
-
重复步骤2, 直到整个数据被遍历
参考资料:蓄水池抽样算法(Reservoir Sampling) - 简书 (jianshu.com)
拒绝采样方法
基本原理:产生具有更大取值范围的等概率随机数,每次只取自己需要的取值范围内的随机数(也是等概率的),在拒绝域的数字需要重新采样。
有这样一个事实 (randX() - 1)*Y + randY() 可以等概率的生成[1, X * Y]范围的随机数(看成Y进制问题)
前半部分描绘出的是第几个Y进制区间,后半部分是Y进制的细刻度变化范围
note: 两个m进制的数字相乘并不是等概率的,如 4 = 1*4 = 2*2 所以想乘的结果中 4 和 7 的结果就不是等概率的
470. 用 Rand7() 实现 Rand10() - 力扣(LeetCode) (leetcode-cn.com)
番外 Py
sortedcontainers库
- OrderedList : 平衡二叉搜索树,即红黑树的内置实现
collections库
- OrderedDIct:哈希表 + 双向链表的结构内部实现,添加的key是按添加顺序排列的,有 move_to_end 方法
itertools库
- itertools.permutations 排列函数
- itertools.combinations 组合函数(无放回抽样)
- itertools. combinations_with_replacement 有返回抽样
bisect库
- bisect.bisect_left( array, tmp ): 找寻的位置是第一个大于等于 tmp 的索引
- bisect.bisect_right( array, tmp ): 找寻的位置是第一个大于 tmp 的索引
- bisect.insort( array, tmp ): 插入排序,保持序列的有序将 tmp 插入 array,保持升序顺序





 浙公网安备 33010602011771号
浙公网安备 33010602011771号