homework2—蒙特卡罗方法手搓图形

整体思路：

1. 导入库

引入numpy用于数值计算与数组操作，matplotlib.pyplot用于绘图。

• 方法：import numpy as np，import matplotlib.pyplot as plt

2. 参数设置

确定椭圆的半长轴长度与用于模拟的随机点数量。

3. 生成随机点

在能覆盖椭圆的x和y轴范围里生成随机点。

• 方法：np.random.uniform

4. 判断点的位置

根据椭圆标准方程判断点是否在椭圆内。

• 方法：通过数组运算(x**2)/(a**2) + (y**2)/(b**2) <= 1

5. 分离内外点

利用布尔索引将椭圆内外的点分开。

• 方法：布尔索引x[is_inside]、x[~is_inside]等

6. 绘制散点图

• 思路：创建画布，分别绘制椭圆内外的随机点。
• 方法：plt.figure、plt.scatter

7. 绘制椭圆边界

用椭圆参数方程生成边界点，再连线绘制椭圆。

• 方法：np.linspace、plt.plot

8. 添加图形元素

为图形添加标题、坐标轴标签等，保证显示效果。

• 方法：plt.title、plt.xlabel、plt.ylabel、plt.axis、plt.grid、plt.legend

9. 显示图形

展示绘制好的图形。

• 方法：plt.show

完整代码：

import numpy as np
import matplotlib.pyplot as plt

# 设置椭圆参数
a = 2.0   # x轴半长轴
b = 1.0   # y轴半长轴
n_points = 50000  # 总点数

# 生成随机点（范围覆盖整个椭圆）
x = np.random.uniform(-a, a, n_points)
y = np.random.uniform(-b, b, n_points)

# 判断点是否在椭圆内（椭圆方程变形）
is_inside = (x**2)/(a**2) + (y**2)/(b**2) <= 1

# 分离内外点
inside_x = x[is_inside]
inside_y = y[is_inside]
outside_x = x[~is_inside]
outside_y = y[~is_inside]

# 创建画布
plt.figure(figsize=(8, 4))  # 调整画布比例适应椭圆形状

# 绘制散点图
plt.scatter(inside_x, inside_y, s=0.1, color='blue', alpha=0.3, label='内部点')
plt.scatter(outside_x, outside_y, s=0.1, color='red', alpha=0.3, label='外部点')

# 绘制理论椭圆边界
theta = np.linspace(0, 2*np.pi, 100)  # 角度采样
plt.plot(a*np.cos(theta), b*np.sin(theta),  # 参数方程
         color='black', linewidth=2, label='真实椭圆')

# 添加图形元素
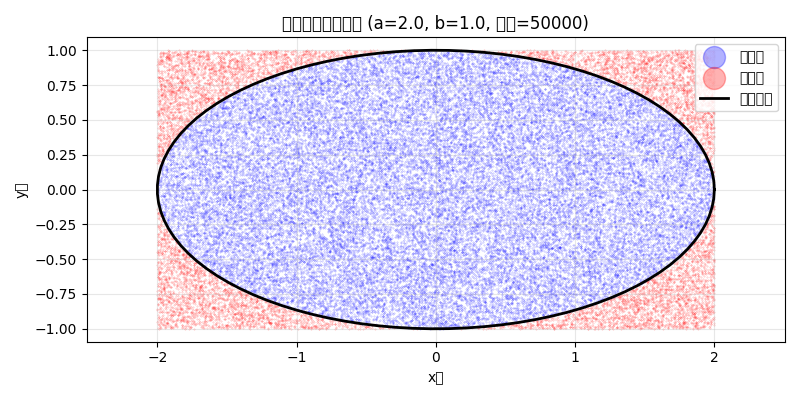
plt.title(f'椭圆蒙特卡罗模拟 (a={a}, b={b}, 点数={n_points})')
plt.xlabel('x轴')
plt.ylabel('y轴')
plt.axis('equal')  # 保持坐标轴比例
plt.grid(alpha=0.3)
plt.legend(markerscale=50)  # 放大图例中的点标记

# 显示结果
plt.show()

运行结果：

• 蓝色点会逐渐在黑色椭圆线内聚集
• 红色点分布在椭圆外红色区域
• 点越多（比如改成100000点），边界越清晰
  (如果想改变椭圆形状，只需修改a和b的值)