oo第一单元总结
第一次作业：
数据管理：
- Polynomial：统一管理表达式，项，因子
- 存储格式：BigInteger[length]
- 运算方法：
- add sub
- mul
- power
- converse（取反）
- 输出方法：print（依次输出正项负项）
解析思路：划分处理
- 预处理：MyString
- delBlank：删除空格
- signPower：将乘方**代换为^便于处理，同时化简**+
- signMul：将*-标记为@，同时化简*+
- simplify：化简多个加减号
- 表达式分析： Term
-
表达式切分：用findAddorSub从右至左寻找第一个非括号内加减号进行划分
-
项切分：用findMul从右至左寻找第一个非括号内乘号进行划分
-
因子切分：用findPower从右至左寻找第一个非括号内乘方进行划分
-
基础因子分析：
- x，常数： 直接建立因子
- 表达式因子：递归调用解析方法建立因子。
-
结构图
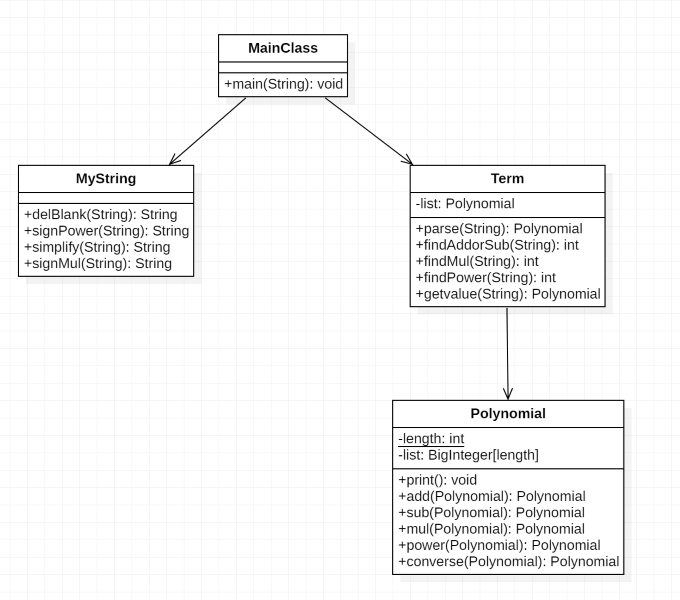
复杂性分析
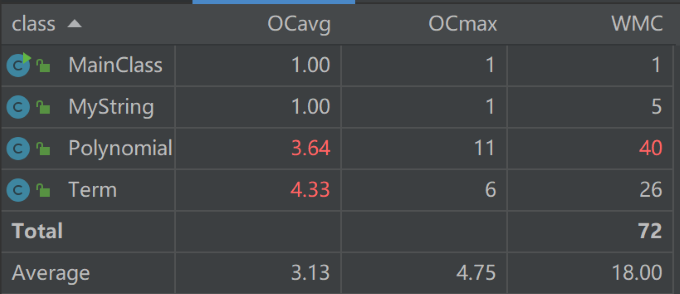
高复杂度在于Term中Parse的重复解析调用
BUG分析：
- 处理次数时只到7次
感想：
- 切分处理的方法相当于从大到小逆向分析表达式结构，为保证正确性需增加大量预处理，同时也极易考虑不周而出错，不利于之后的迭代开发。
第二次作业：（重构）
数据管理：
- Term：管理单个项
- 存储格式：
- BigInteger：系数与次数
- ArrayList
：三角函数因子 - ArrayList
：三角函数次数
- 运算方法：
- mul
- judge（判断相等）
- 输出方法：getString
- 存储格式：
- Terms：统一管理表达式，项，因子
- 存储格式：ArrayList
- 运算方法：
- add sub
- mul
- power
- converse（取反）
- buildSin buildCos
- 输出方法：getString
- 存储格式：ArrayList
解析思路：递归下降
- 预处理：MyString
- delBlank：删除空格
- simplify：化简多个加减号
- sign：将乘方**代换为^便于处理，同时化简**+
- 表达式分析： Parser
- 表达式分析：用parseExp将表达式解析为项的加减
- 项分析：用parseTerm将项解析为因子相乘
- 因子分析：Lexer
- x，常数：直接建立因子
- 三角函数，表达式因子：递归调用解析方法建立因子
- 函数因子，表达式因子：将形参替换为实参后递归调用解析方法建立因子
结构图
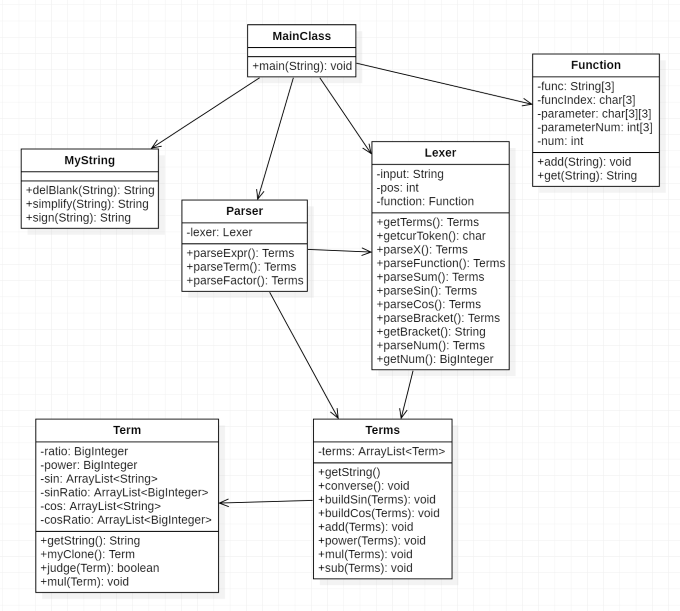
复杂性分析
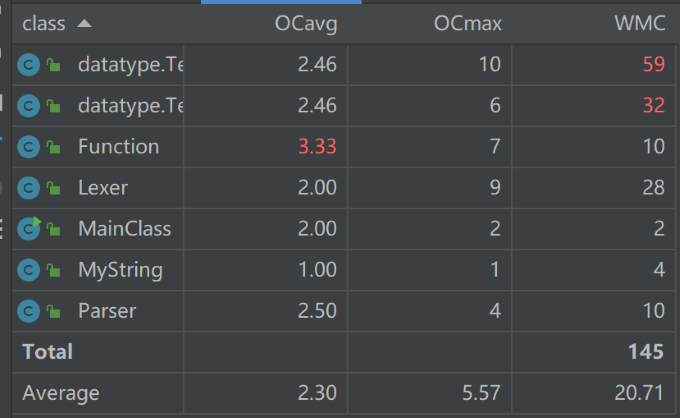
高复杂度在于Function的解析
BUG分析：
- cos(0) = 1
- 解析实参时当作无符号解析
整体分析：
- 递归下降这种由小及大的分析方法逻辑很正，分析的正确性有十足的保证。大概是第一次作业尝到了甜头，第二次作业也采用统一化的存储格式，但实际上这也抹去了不同因子的特征，之后的迭代开发。此外深克隆的问题也着实困扰了我许久，也明确了什么类型是指针，什么是实体。
第三次作业：（迭代）
数据管理：
- 同第二次
解析思路：递归下降
- 同第二次，仅在获取实参时递归调用解析函数
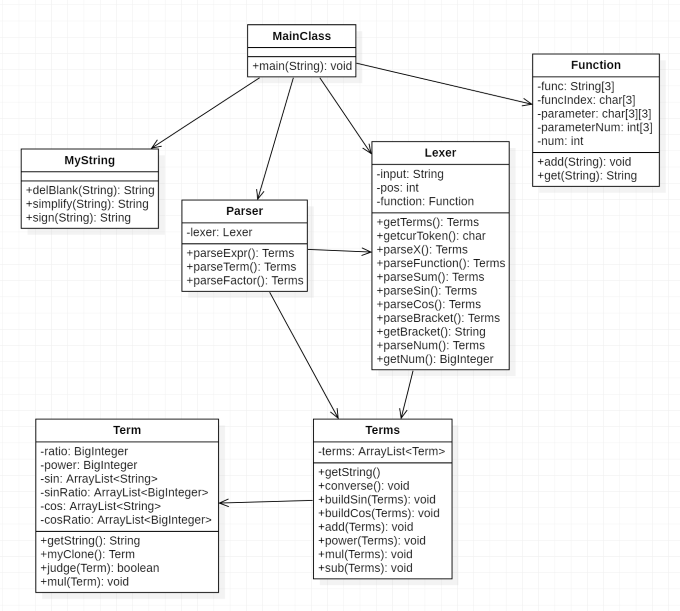
结构图
- 同第二次
复杂性分析
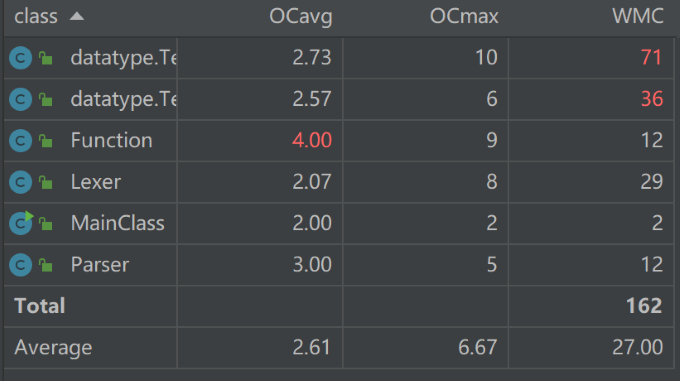
高复杂度在于Function的递归调用
BUG分析：
- 三角嵌套因子格式错误
- 带入实参时未加括号
- 合并嵌套三角因子有误
整体分析：
- 结构固定后的迭代开发不会耗费多少时间，因而前期的问题分析建模远比码代码重要。但自己仍然是一种面向过程的思维模式，对类的划分仅仅停留在功能层面。（若不是训练的提示我自己就一定不会从逻辑层面将Lexer和Parser分开。）过去只注重能否解决问题，现在要更加注重解决的过程。
