人工智能

一 人工智能基本概念

1 机器学习基本概念

模拟人类学习行为，完善自身性能预测人类活动
机器学习模型=数据+机器学习算法

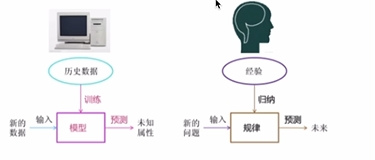
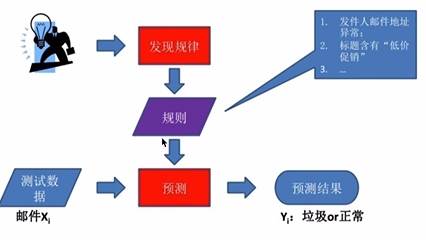
2 基于规则学习

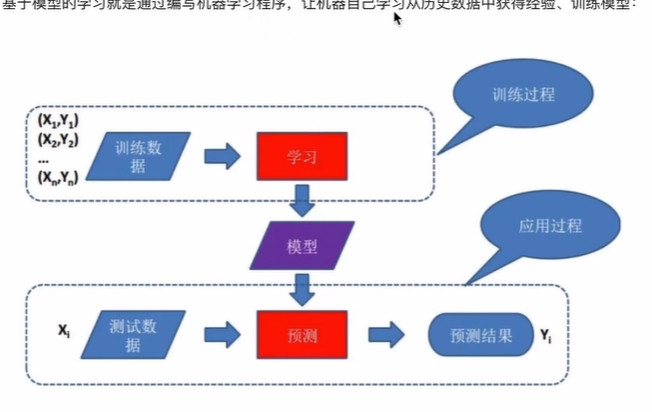
3 基于模型去学习

通过编写程序，让机器自己学习从历史数据获得经验，形成模型，用模型再去预测数据。

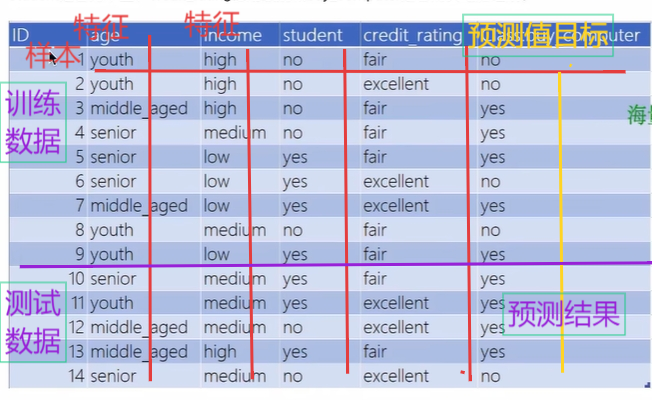
4 机器学习数据集描述

5 扩展

用向量对数据进行表示（涉及线性代数知识）

注释：X的上标代表样本，下标代表特征。

6 小结

（1）基于规则的学习是使用一组“if else”规则来对样本进行分类的技术
（2）基于模型的学习是从数据集中学习来获取模型知识通过模型来对样本进行分类技术
（3）机器学习的数据集：样本，特征，目标，训练集，测试集。

二 机器学习分类

1.监督学习
2.无监督学习
3.半监督学习
4.强化学习

1 监督学习

人们给机器一大堆标记（标记的意思是提前预测的目标值）好的样本比如：
一大堆照片，标记是否是猫。
让机器学习归纳出算法或模型（函数,规律）。
使用该算法模型预测没有标记的照片是否是猫。
监督学习模型：线性回归（linear regression），逻辑回归（logic regression），svm，神经网络(Neural network)。

1.1 分类问题

分类问题是监督学习的核心问题
当输出值（目标值）是有限个值时，预测问题便成为分类问题
分类器：监督学习从数据中学习的一个分类模型或决策函数。
分类：分类器对新输入进行输出的预测值。
分类问题包括学习过程和分类过程
学习过程：根据训练集数据利用有效的学习方法学习一个分类器。
分类过程：利用学习的分类器对新的数实例进行分类。
例子：

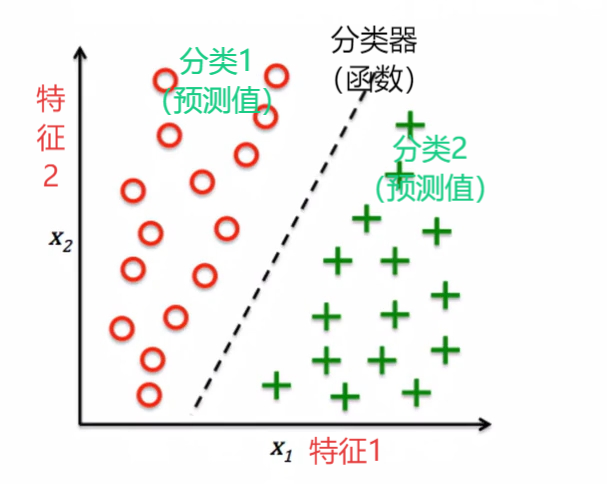
邮件分类 分成垃圾邮件和好邮件（两个目标值）
有30个训练集样本 15个标记好15个标记垃圾
数据是二维的，意味着每个样本都有2个特征值
监督学习算法得到一条规则，将两种样本分开，可以根据新的样本划分到某个类别中
二分类问题：输出变量有两个
多分类问题：输出变量有两个以上

1.2 回归问题

分类问题：输出的变量是离散的
回归问题：输出的变量是连续的，在回归分析中找到自变量（特征值）和因变量（输出值）之间的关系

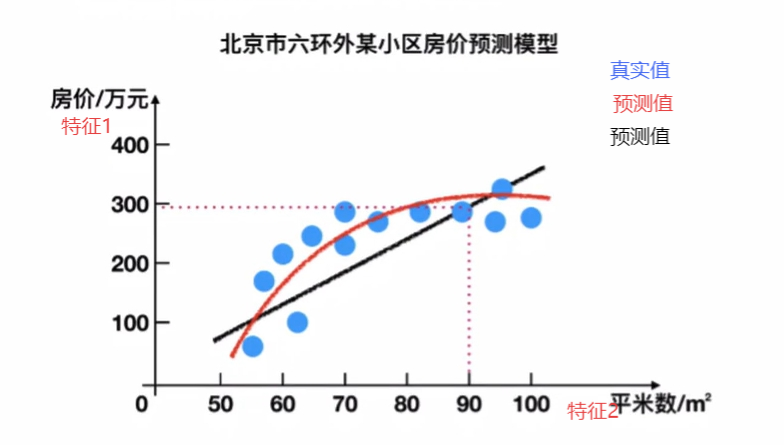
根据实际点到直线的平均平方距离的最小，从而绘制了两条拟合曲线。
回归问题的分类：
根据输入变量的个数（特征值）分为一元（一个特征值）回归和多元回归。上图为多元回归
输入变量和输出变量之间的关系分为线性回归（一条直线）和非线性回归。

2无监督学习

人们给机器没有分类标记的数据，机器对数据进行分类检测异常

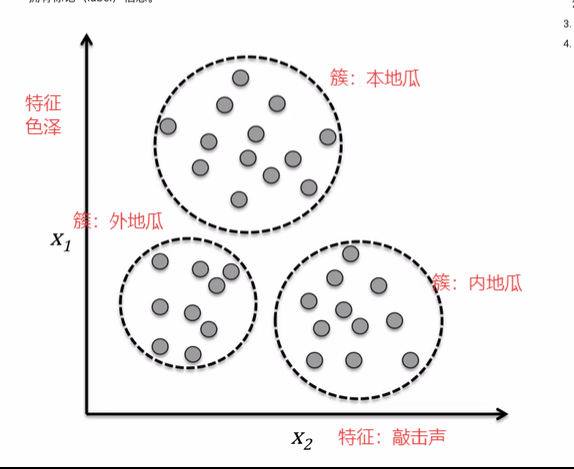
2.1 聚类问题

在分类之前没有标签（特征），根据相似性将数据划分为不同的簇

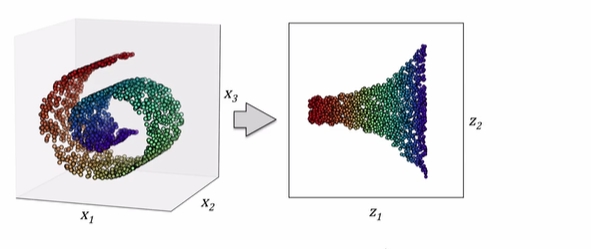
2.2 数据降维

用于数据特征的预处理，能够最大程度保留信息并压缩数据到维度较小的维度， 3维到2维

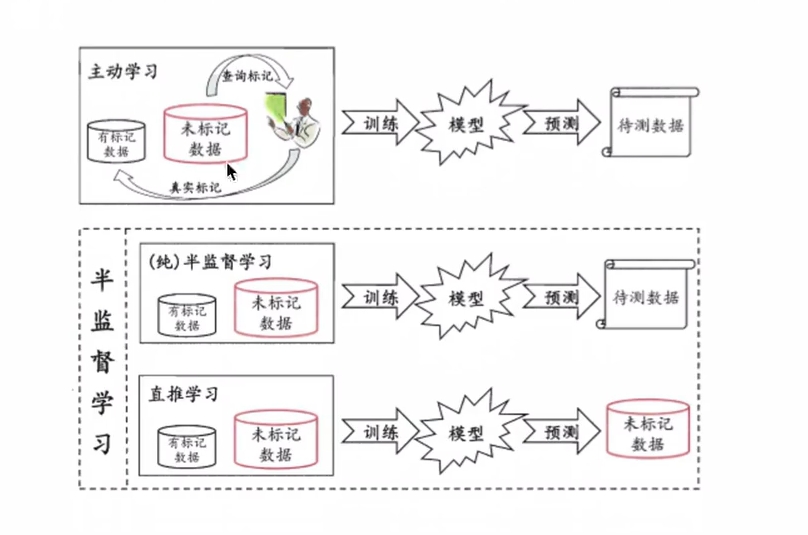
3 半监督学习

给机器的数据有标记的训练出模型用于对未知数据进行预测
根据是否有专家互动分为主动学习和半监督学习
半监督学习：
纯半监督学习：用标记好的数据和没有标记的数据用都用作训练集
直推学习：无标记的数据用作预测

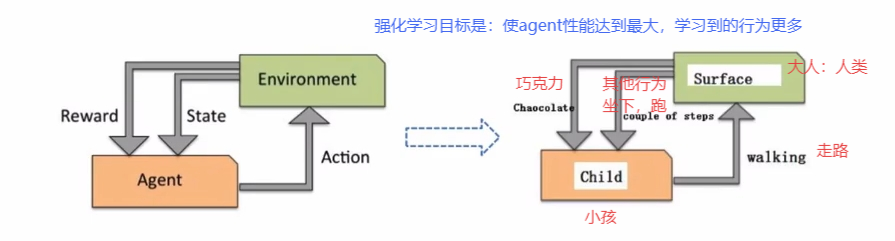
4 强化学习

主要用来解决连续决策问题（alphgo）
目标是变化的，不存在绝对正确的标签

三 拟合问题

1 欠拟合
2 过拟合
3 泛化能力

1 欠拟合

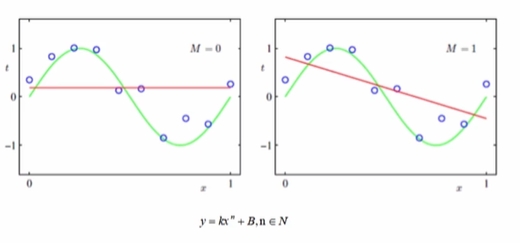
现象：训练集上表现效果差，拟合结果表现也差
原因：模型过于简单（函数过于简单，参数少，特征少）
解决办法：增加特征，减少正则化参数，增加模型复杂程度

2 过拟合

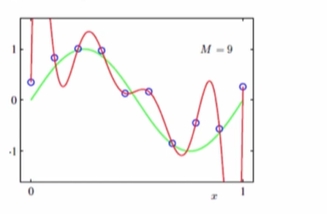
原因：模型太复杂，数据不蠢
出现的场景：模型优化到一定程度，就会出现过拟合
解决办法：
1 重新清洗数据
2 增大训练数据量
3 采用正则
4 droput:采用随机采样的方法训练模型，常用于神经网络算法；

3 奥卡姆剃刀原则

给两个具有相同泛化误差的模型选择模型简单的

4泛化能力

学得的模型能很好的适用于“新样本”， 学得模型适用于新样本的能力叫做泛化能力
//过拟合和欠拟合是机器学习算法表现差的两大原因

四机器学习开发环境

1 机器学习开发框架

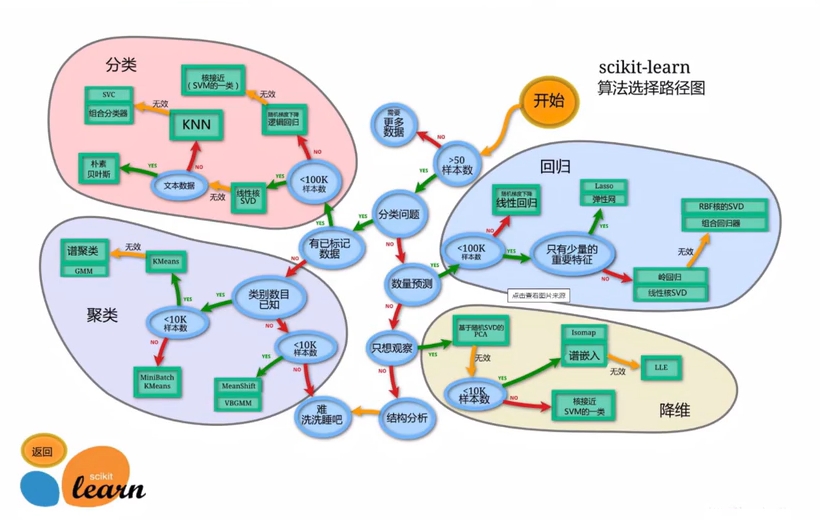
基于python的scikit-learn库
（此库建立在numpy,scipy,matplotlib上）
里面封装了分类算法，回归算法，聚合算法也可以去进行降维，模型选择，数据预处理。
流程图：

五 k邻近

1 为什么学习KNN算法

knn是监督学习分类算法，解决现实生活中分类问题。
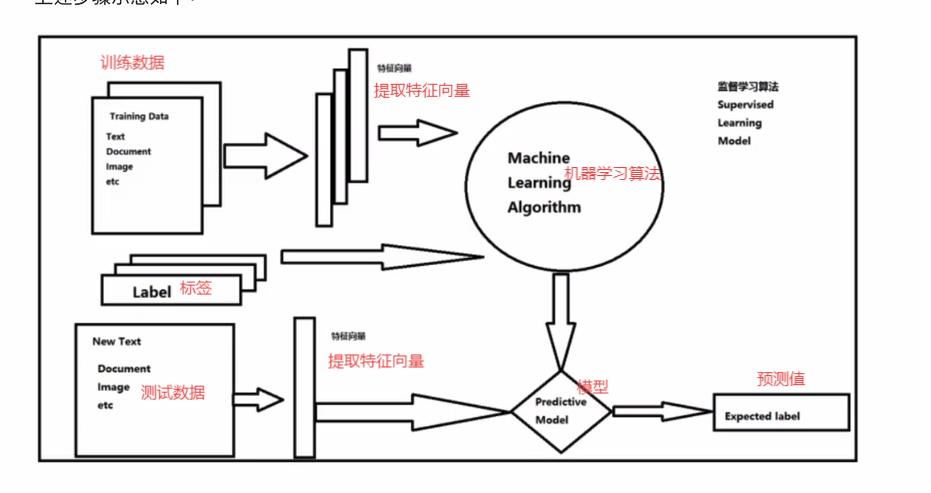
监督基本流程：
（1）准备数据（视频，文本，图片）
（2）抽取所需要的特征，形成特征向量
（3）将特征向量连同标记（lable）一并送入机器学习算法->训练出一个预测模型
（4）采用同样的特征提取方法用于测试数据，得到用于测试的特征向量
（5）使用预测模型对这些待测的特征向量进行预测并得到结果；

2 KNN原理（k邻近算法）

k邻近就是找到距离最近的k个点来决定测试数据

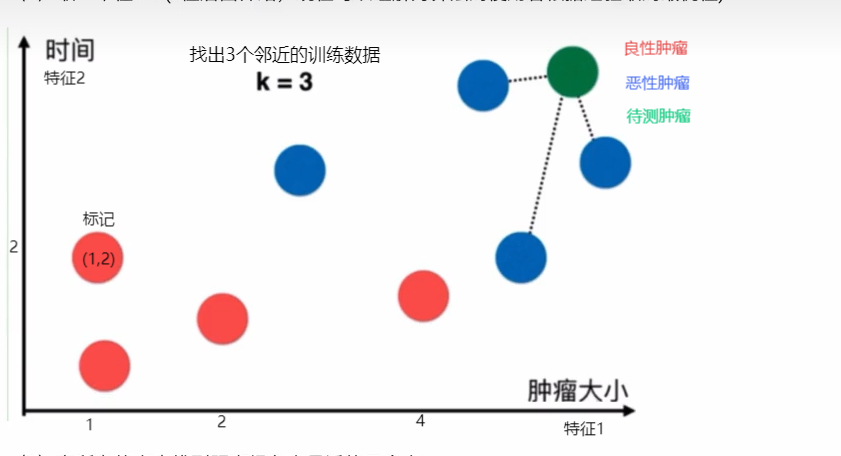
k=3
最近的3个事恶性肿瘤所以待测的也是恶性肿瘤。

2.2算法原理

三要素
1.距离度量
2.k值选择
3.分类决策准则（常用：少数服从多数）

3 距离度量

3.1 机器学习中为什么要度量距离？

经常需要判断两个样本之间是否相似（如knn k-means等），通常将相似的判断福安转换成距离的计算。 KNN算法要求数据的所有特征都用数值表示，若存在非数值类型，必须采用手段将其量化为数据。

3.2 欧氏距离

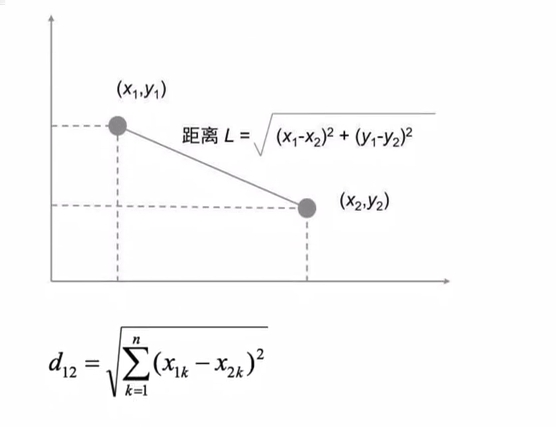
3.3 曼哈顿距离

求两点之间|x1,x2|之间距离再算|y1与y2|之间的距离然后求和。

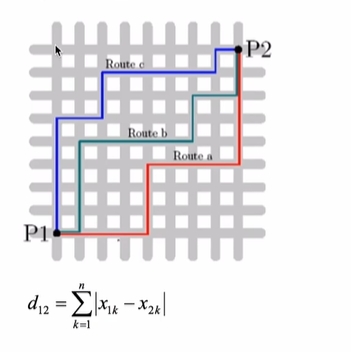
3.4 切比雪夫距离

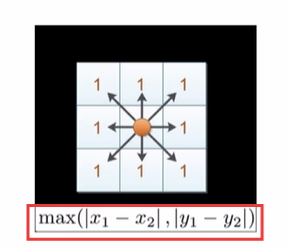
3.5闵式距离

闵式距离不是一种距离，而是一组距离的定义，是对多个距离量公式的概括性的表述。

4 归一化和标准化

4.1 为什么做归一化和标准化

二选一；

4.2归一化

通过对原始数据进行变换，把数据映射到（0,1）之间。（归一适合传统精确小数据的场景）

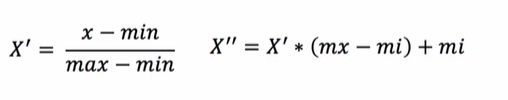
from sklearn.preprocessing import MinMaxScaler
def test()
{ #1准备数据
	data=[[90,2,10,40],
		[60,4,15,45],
		[75,3,13,46]]
	#2 初始化归一化对象
	transformer=MinMaxScalar()
	#3对原始特征数据进行归一化处理
	data=transtransformer.fit_transform(data)
	#4 打印归一化之后的结果
	print(data)
}

4.3 标准化

from sklearn.preprocessing import StadardScaler
def test()
{ #1准备数据
	data=[[90,2,10,40],
		[60,4,15,45],
		[75,3,13,46]]
	#2 初始化标准化对象
	transformer=StadardScaler()
	#3对原始特征数据进行变换
	data=transtransformer.fit_transform(data)
	#4 打印标准化之后的结果
	print(data)
}
如果出现异常点，少量的异常点对平均值的影响并不大