noi 2019 瞎写写

A 回家路线

平方 \(\rightarrow\) 斜优，拆开柿子随便做做就好了。

B 机器人

拉格朗日插值：

\[f(k)=\sum_{i=0}^{n}y_i\prod_{i\neq j}\dfrac{k-x_j}{x_i-x_j} \]

直接计算是 \(\mathcal{O}(n^2)\) 的，当 \(x\) 是连续的一段整数时可以做到 \(\mathcal{O}(n)\)，具体地，\(\prod_{i\neq j}\dfrac{k-x_j}{x_i-x_j}\) 的分子分母其实都是一段连乘积挖去一个数，可以通过预处理前后缀积快速求值。

---

这题放在 d1T2 还是太超前了。

对于 P 型机器人而言，将它放在 \(i\) 之后它会走到左边第一个严格 \(>a_i\) 的位置，对于 Q 型机器人而言，将它放在 \(i\) 之后它会走到右边第一个 \(\geq a_i\) 的位置。

显然一个 \(a_i\) 只会影响它作为最大值的一段区间，我会区间 dp！

瞎设计 dp 状态是没有前途的，我们的状态一定要能够简单地满足题目中的限制，或者说后面的决策不会影响前面已经决定了的是否满足限制，\(dp_{l,r,k}\) 表示 \(a[l,r]\) 区间中最大值为 \(k\)，并且 \(a_{l-1}>k,a_{r+1}\geq k\) 的方案数，这样设计状态方便我们把限制的判断拆分到转移中进行。

枚举最大值所在的最靠后的位置 \(t\) 进行转移，\(dp_{l,r,k}\) 能从 \(t\) 转移的充要条件是 \(|(t-l)-(r-l)|\le2\wedge k\in[A_t,B_t]\)，容易得到满足条件的 \(t\) 的数量级在 \(\mathcal{O}(1)\) 级别，设 \(sum_{l,r,k}\) 表示 \(dp\) 的前缀和可以优化转移到 \(\mathcal{O}(n^2A)\)，可以获得 35pts。

简单观察可以发现有用的区间数是极少的，写一发搜索发现只有 \(2518\) 个，用记搜实现 dp 拿到 50pts。

继续想部分分，11 ~ 12 的点保证了 \(A_i=1,B_i=10^9\)，这样就不需要考虑 \(k\in[A_t,B_t]\) 的条件，把值域从状态中去掉可以用多项式表示 dp 数组，从初始状态 \(l=r\) 开始分析，此时 \(dp_{l,r,k}=1,sum_{l,r,k}=k\)，显然\(dp_{l,r}\) 是关于 \(k\) 的 \(0\) 次式，\(sum_{l,r}\) 是关于 \(k\) 的 \(1\) 次式，于是按照转移方程 \(r=l+1\) 时 \(dp_{l,r}\) 是关于 \(k\) 的 \(1\) 次式，归纳可得 \(dp_{l,r}\) 是关于 \(x\) 的 \(r-l\) 次式，\(sum_{l,r}\) 是关于 \(x\) 的 \(r-l+1\) 次式，可以先求出 \(sum_{1,n}\) 的前 \(n\) 项的值，用拉插可以 \(\mathcal{O}(n)\) 求出答案，时间复杂度 \(\mathcal{O}(2518 n)\)，又水了 10pts。

上面的做法要求没有 \(k\in[A_t,B_t]\) 的条件，其实我们可以通过枚举当前转移的值域区间去掉这一限制，实现时将所有右端点 \(+1\) 并和左端点一同离散化到有序数组 \(C\) 中，每次枚举一个区间 \([C_i,C_{i+1})\) 作为当前转移的值域区间，对于有意义的 \(l,r\) 求出 \(sum[C_i,C_i+r-l]\) 的点值，转移时注意 \([A_t,B_t+1)\) 要包含当前转移的值域区间，每次做完一个区间的 dp 后拉插求出 \(sum_{l,r,C_{i+1}-1}\)，反复进行以上过程直到遍历完 \(C\)，时间复杂度 \(\mathcal{O}(2518 n^2)\)。

• 划分状态时尽量贴近限制设计，这样做的好处是可以把限制简单地放在转移时讨论。
• 需要把值域从状态中剔除时考虑用多项式表示 dp 数组。

C 序列

明显比 T2 简单。

网络流建模中至少是不好表示的，把至少有 \(L\) 对下标相同先转化成至多有 \(K-L\) 对下标不同，

建模：

以下用 \(f\) 表示容量，\(w\) 表示费用。

建立虚点 \(u,v\) 用来限制下标不同的对数，连边 \(u\rightarrow v,f=K-L,w=0\)，这条边上的流量称为自由流量。

对于每个 \(i\) 连边

• \(st\rightarrow a_i,f=1,w=a_i\)
• \(b_i\rightarrow ed,f=1,w=b_i\)
• \(a_i\rightarrow b_i,f=1,w=0\)，表示选择一对相同的下标
• \(a_i\rightarrow u,f=1,w=0\)
• \(v\rightarrow b_i,f=1,w=0\)，以上两条表示 \(a_i/b_i\) 在一对不同下标的选择中

暴力费用流可以拿到 64pts。

---

这个图长得一脸二分图样其实就是图比较简单，考虑模拟费用流，EK 有经典结论与 \(st\) 和 \(ed\) 相连的边不会被退流，所以需要讨论的增广路数量不多。

把所有的增广路转化成一些配对关系的变化后主要有以下五种，下图中红色为新选择的点，黑色为已选的点。绿色边为原来的配对，红色边为新的配对。

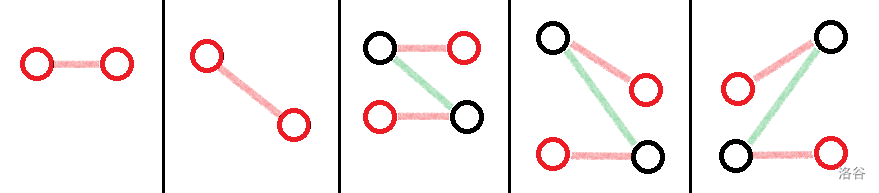
从 cmd 那里盗的图 qwq

假设这一轮选择的是一对均未被选择的 \((a_i,b_j)\)，已经被选择的点属于集合 \(G\)，形式化的说有以下五种方案

1. \(i = j\)
2. \(i\neq j\)，消耗一流量的自由流量。
3. \(b_i,a_j\in G\)，将 \(a_i\) 与 \(b_i\) 配对，\(a_j\) 与 \(b_j\) 配对，增加一流量的自由流量
4. \(b_i\in G\)，将 \(a_i\) 与 \(b_i\) 配对，\(b_j\) 与原来与 \(b_i\) 配对的 \(a_k\) 配对
5. \(a_j\in G\)，将 \(a_j\) 与 \(b_j\) 配对，\(a_i\) 与原来与 \(a_j\) 配对 的 \(b_k\) 配对

用堆维护以上转移，\(q_0\) 维护未选的 \(a_i+b_i\) 的最大值，\(q_{a,0},q_{b,0}\) 分别维护未选的 \(a,b\) 的最大值，\(q_{a,1},q_{b,1}\) 维护本侧未选中另一侧被选中的值的最大值。

分别记五个堆的堆顶为 \(s,a_0,b_0,a_1,b_1\)，则以上五种情况的贡献可以被表示

1. \(s\)
2. \(a_0+b_0\)，仅当有自由流量时
3. \(a_1+b_1\)，自由流量 \(+1\)
4. \(a_0+b_1\)
5. \(a_1+b_0\)

一次增广对五种方案取 max 计入答案，时间复杂度 \(\mathcal{O}(n\log n)\)。

• 网络流建模时可以先看看能不能把至少的限制转化成至多，如果不能再考虑上下界网络流你聪明的告诉我，上下界网络流怎么模拟费用流呢。

D 弹跳

暴力 72pts 真香。

观察到权值都在点上，对于 dij 有经典结论是一个点只会被松弛一次，线段树维护第一维，set 维护第二维，每次暴力松弛即可。

E 斗主地

我会暴力 dp！

设 \(dp_{i,j}\) 表示选了左边 \(i\) 张牌，右边 \(j\) 张牌的概率，转移是 trivial 的，可以拿到 30pts。

观察一下转移，\(i\) 位置上的值会对洗牌后 \(j\) 位置上的期望产生一个常数倍的贡献，可以猜测洗牌后的期望仍然是一个多项式函数且按照数据范围来说次数是相同的不然就没法做了，每次求出二次函数的前三项解出系数即可。

证明咕咕咕。

F I 君的探险

杨戬提答。