并查集

 

　　当给出两个元素满足等价关系构成一个无序对(a，b)时，需要快速“合并”a和b分别所在的集合，这其间需要反复“查找”某元素所在的集合。“并”、“查”和“集”三字由此而来。

　　可以采用有根树表示集合，树中的每个结点包含集合的一个元素，每棵树表示一个集合。多个集合形成一个森林，以每棵树的根结点编号唯一标识该集合，并且根结点的父结点指向其自身，树上的其他结点都用一个父指针它的附属关系。

 

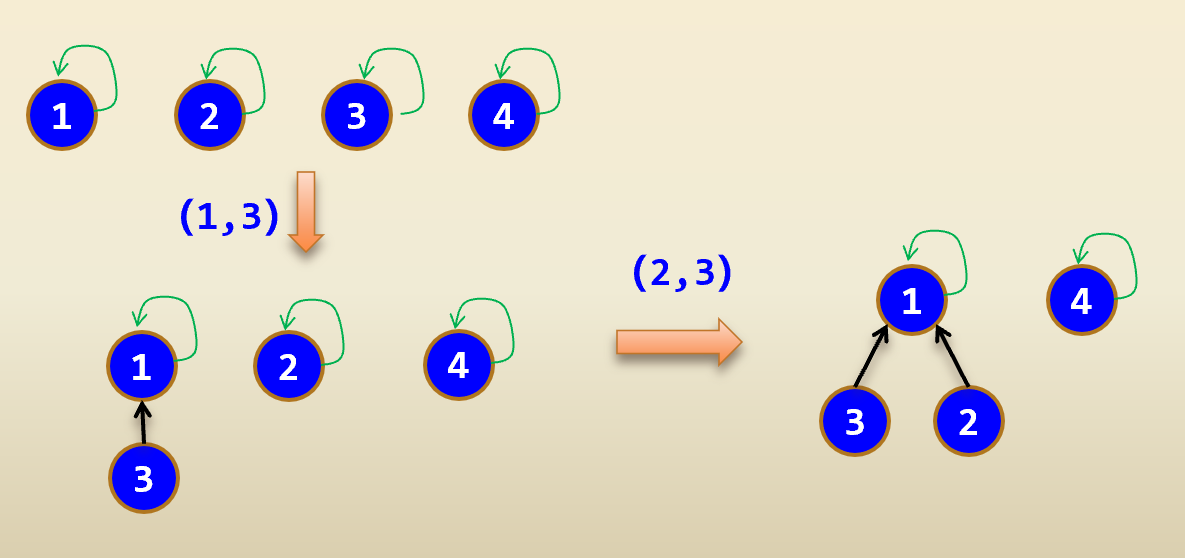
 利用数组t来存储森林，每个结点定义为一个结构体，要保存三个信息，自身结点的值，所在的高度，以及前置结点

typedef struct node
{
        int data;//结点的值
        int rank;//秩
        int parent;//前置结点
}UFSTree;

首先要初始化每个结点，

void MAKE_SET(UFSTree t[],int n)
{
      for(int i=0; i<n;i++)
      {
            t[i].rank=0;
            t[i].parent=i;
       }  
}

然后要有查询的操作

int Find_SET(UFSTree t[],int x)
{
     if(t[x].parent!=x)
        return Find_SET(t,t[x].parent) //递归找x的父结点
     else  //当x等于x的父结点时
        return x;  
}

合并集合

void UNION(UFSTree t[],int x,int y)//x,y所在的子树合并
{
        x=Find_SET(t,x);
        y=Find_SET(t,y);
        //按秩合并
        if(t[x].rank>t[y].rank)//x的秩大于y的秩
           t[y].parent=x;
        else//y的秩大于等于x的秩
        {
           t[x].parent=y;
           if(t[x].rank==t[y].rank)
              t[y].rank++;
         }
}