阶 原根 离散对数
阶 原根 离散对数
阶
定义
\(a\mod p\) 的阶是 \(a^e\equiv1\pmod p\) 的最小指数 \(e\)
符号语言: \(\delta_p(a)\) 代表 \(a\) 在 \(\mod p\) 的意义下的最小指数 \(e\) 使\(a^e\equiv1\pmod p\)
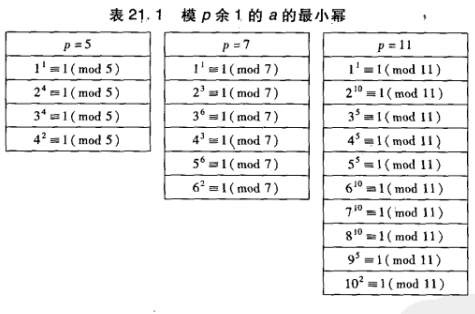
根据这个表格，我们可以举出一些例子
原根
定义
满足上述则 \(a\) 是 \(\mod m\) 意义下的原根
最小原根 \(g\)
我们枚举，如果 \(gcd(now,n)\ne1\) 那一定不是原根
找出一个可能是原根的数，我们从 \([1-\varphi(n))\) 枚举每个 \(k\) 判断 \(now^k\equiv1\pmod m\) 是否成立
如果全都不同余 \(1\) ，那么就找到了 \(g\) ，可以容易的找出其他原根：
while(++g){
int now=1,bj=0;
if(gcd(g,n)!=1) continue;
for(int j=1;j<phi[n];j++){
now=now*g%n;
if(now==1){
bj=1;
break;
}
}
if(bj==1) continue;
else if(bj==0){
break;
}
}
找出其他原根
我们认为 \(g\) 是最小的原根
寻找方法：
我们考虑当 \(gcd(k,\varphi(m))=g\) 的时候 \({g^{k}}^{\frac {\varphi(m)} {k}}\) 会同余 \(1\)
代码
int now=g;
ans[++cnt]=g;
for(int j=2;j<phi[n];j++){
now=now*g%n;
if(gcd(j,phi[n])!=1) continue;
ans[++cnt]=now;
}
有无原根
这些数有原根
\(结论：2,4,p^k,2×p^k，其中 p 为奇素数，k 为正整数。\)
证明详见
原根数量
我们在前面可以知道，当求出一个g(最小原根)，
有多少个 \(k\) 满足:\(k\in[1,\varphi(m))~~~gcd(k,\varphi(m))=1\)
其实就是 \(\varphi(\varphi(m))\)
总代码：
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int phi[N],prim[N],v[N],vis[N],tot=0,ans[N],cnt=0;
int t,n,d;
void pre(){
phi[1]=1;
for(int i=2;i<=N-1;i++){
if(!v[i]){
prim[++tot]=i;
phi[i]=i-1;
}
for(int j=1;j<=tot&&prim[j]*i<=N-10;j++){
v[i*prim[j]]=1;
if(i%prim[j]==0){
phi[i*prim[j]]=phi[i]*prim[j];
break;
}else{
phi[i*prim[j]]=phi[i]*phi[prim[j]];
}
}
}
vis[2]=1;
vis[4]=1;
for(int i=2;i<=tot;i++){
for(long long j=1;j<=N;j=j*prim[i]){
if(j>N-10){
break;
}
vis[j]=1;
if(2*j<=N-1) vis[2*j]=1;
}
}
}//预处理phi和prime
int gcd(int x,int y){
if(y==0) return x;
return gcd(y,x%y);
}
void input(){
scanf("%d",&t);
for(int i=1;i<=t;i++){
cnt=0;
memset(ans,0,sizeof(ans));
scanf("%d%d",&n,&d);
if(!vis[n]){
printf("0\n\n");
continue;
}
int g=0;
while(++g){
int now=1,bj=0;
if(gcd(g,n)!=1) continue;
for(int j=1;j<phi[n];j++){
now=now*g%n;
if(now==1){
bj=1;
break;
}
}
if(bj==1) continue;
else if(bj==0){
break;
}
}
int now=g;
ans[++cnt]=g;
for(int j=2;j<phi[n];j++){
now=now*g%n;
if(gcd(j,phi[n])!=1) continue;
ans[++cnt]=now;
}
sort(ans+1,ans+1+cnt);
printf("%d\n",phi[phi[n]]);
for(int j=1;j<=phi[phi[n]]/d;j++){
printf("%d ",ans[j*d]);
}
printf("\n");
}
}
int main(){
// freopen("1.txt","w",stdout);
pre();
input();
return 0;
}
离散对数
就是对数的定义，只不过在模意义下
定义
对于正整数 \(p\) , \(p\) 的原根 \(g\) ，整数 \(b\)，使得 \(g^x\equiv b \pmod {p}\) 则称 \(x\) 为 \(b\) 的离散对数，记作
\(\log_g(b)\)
性质
1.当 \(p\) 为质数时，\(∀i ∈ [0, p − 1]\) 在 \([0, p − 1]\) 范围内都有唯一对应的离散对数。
2.当 \(p\) 为奇质数的幂时，\(p\) 的倍数不存在离散对数，通常需要特殊处理。\(2p^ k\) 也类似。
利用离散对数可以将模 \(p\) 意义下的 \(xy\) 转化为 $ g^{\log_g
(x)+\log_g
(y)}$
BSGS
题目描述：
已知 \(a,b,p\)，求模 \(p\) 意义下 \(x=\log_a(b)\) ，保证 \(p\) 为质数 。
根据性质1，在 \(x\in[1,m]\implies b\in[1,m]\)
我们枚举 \(x\) ，可以得到答案，但时间复杂度不能接受
我们考虑更优秀的枚举：
\(设x=A\times\sqrt m-B(A,B\in[1,{\sqrt m}])\)
可以发现现在依旧 \(x\in[1,m]\)
转换一下
发现现在只有两个未知数A,B我们可以先枚举一次B预处理
用map记录所有 \(b \times a^B~ mod~m\)
再枚举A算出 \(a^{A*\sqrt m}~mod~m\) 在map找找有没有对应的
