学习记录2复杂度的渐进表示

复杂度的渐进表示法
O(f(n))用于表示某种上界，存在Ω(f(n))用于表示某种下界，还会出现上下界等价的情况
上下界不是唯一的，分析算法的效率通常是希望上届或下届与真实情况能够贴近，所以我们找以我们的能力允许找到的最大或最小

不同函数的复杂度

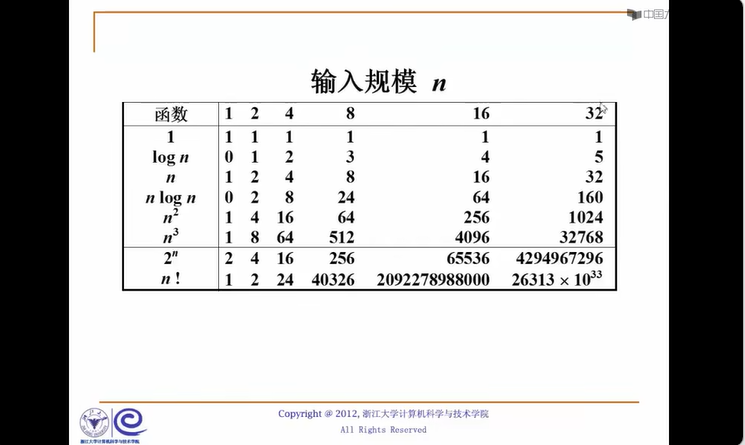
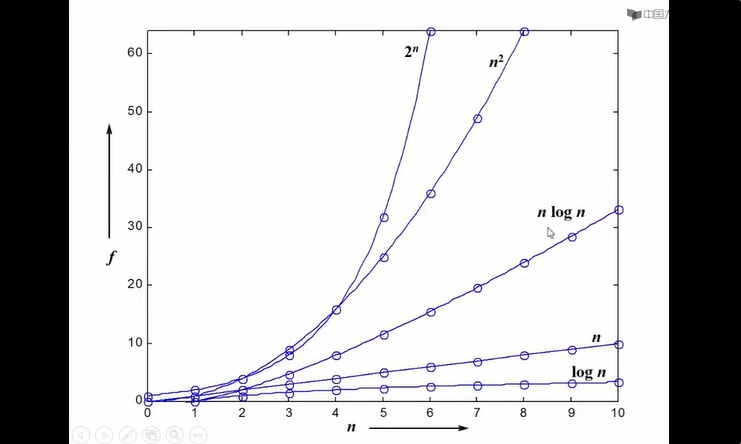
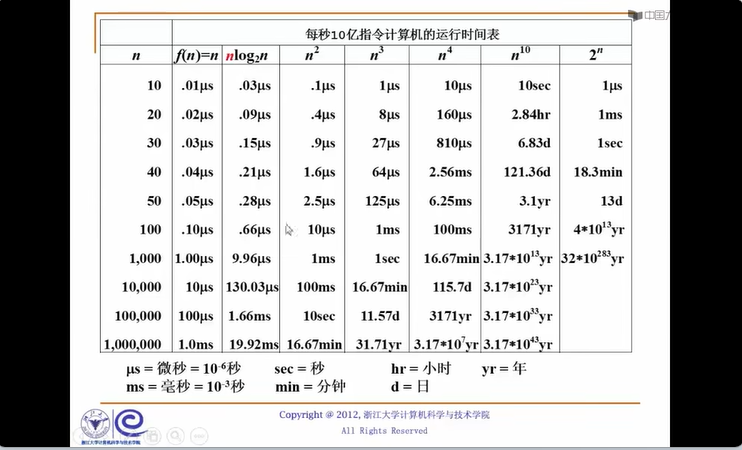
在设计算法时千万要尽量降低复杂度，可以用低复杂度去代替高复杂度的函数，以提高算法的效率
复杂度分析小窍门
知道两段算法的上界，那两段算法的总时间T1(n)+T2(n) = max(O(f1(n)),O(f2(n))),上界就是复杂度高的哪一个；当两个算法嵌套起来时，总时间T1(n)T2(n) = O(f1(n)f2(n)),上界就是它们上界的乘积；n的k阶多项式，起作用的就是最大的那一项n^k；for循环的时间复杂度(T(n))(/font)等于循环次数乘以循环体代码的复杂度