pytorch深度学习实战:全连接神经网络图像识别
1. 实践目标:区分图片中的鸟和飞机
2. 加载数据
在做下述步骤前,首先加载数据:
from torchvision import datasets
data_path = './data/CIFAR-10/'
cifar10 = datasets.CIFAR10(data_path, train = True, download = True)
cifar10_val = datasets.CIFAR10(data_path, train = False, download = True)
2.1. 将PIL图像转换为张量
接着,需要将加载的数据转化为 张量(tensor)的形式,这可以通过ToTensor实现。
ToTensor 将 NumPy 数组和 PIL 图像变换为张量。它还将输出张量的尺寸设置为 C×H×W(通道、高度、宽度),如下:
from torchvision.transforms import ToTensor
# 简单加载一个数据集作为示例,传入PIL
cifar10 = datasets.CIFAR10(data_path, train = True, download = True)
# 将PIL图像转换为张量
img, label = cifar10[99]
to_tensor = ToTensor()
img_t = to_tensor(img)
print(img_t.shape) # torch.Size([3, 32, 32])
亦能将ToTensor直接作为参数传递给datasets.CIFAR10
cifar10 = datasets.CIFAR10(data_path, train = True, download = True, transform = ToTensor())
补充:
permute 函数用于改变张量的维度顺序。在这个例子中,img_t.permute(1, 2, 0) 将张量从 C×H×W 变换为 H×W×C,这是 matplotlib 显示图像的要求。如下:
plt.imshow(img_t.permute(1, 2, 0)) # C x H x W -> H x W x C
plt.show()
2.2. 归一化
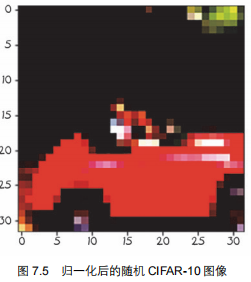
接着,在输入神经网络之前,对输入数据进行归一化。归一化的目的是将输入数据的特征值缩放到一个相似的范围,以避免某些特征对模型训练的影响过大。
首先,计算平均值和标准差:
imgs = torch.stack([img_t for img_t, _ in cifar10], dim = 3) # torch.Size([3, 32, 32, 50000]) <- 堆叠到了最后一维
imgs_mean = imgs.view(3, -1).mean(dim = 1) # 对每个通道求平均值
imgs_std = imgs.view(3, -1).std(dim = 1) # 对每个通道求标准差
输出:
print(imgs_mean) # tensor([0.4914, 0.4822, 0.4465])
print(imgs_std) # tensor([0.2470, 0.2435, 0.2616])
通过Compose将归一化连接到ToTensor,
transform = Compose([ToTensor(), Normalize(imgs_mean, imgs_std)])
最终,实际的加载数据代码如下:
# -----------------------------------------------------------------------
# 加载数据
from torchvision import datasets
from torchvision.transforms import ToTensor # PIL (0~255) -> Tensor (0.0~1.0)
from torchvision.transforms import Normalize # 归一化
from torchvision.transforms import Compose # 组合多个变换
data_path = './data/CIFAR-10/'
transform = Compose([ToTensor(), Normalize((0.4914, 0.4822, 0.4465), (0.2470, 0.2435, 0.2616))])
transformed_cifar10 = datasets.CIFAR10(data_path, train = True, download = True, transform = transform)
transformed_cifar10_val = datasets.CIFAR10(data_path, train = False, download = True, transform = transform)
# -----------------------------------------------------------------------
# 展示图像
import matplotlib.pyplot as plt
img_t, _ = transformed_cifar10[99]
plt.imshow(img_t.permute(1, 2, 0))
plt.show()
2.3. 提取鸟和飞机的图像
针对我们的时间目标,提取出鸟和飞机的图像。如下:
# -----------------------------------------------------------------------
# 一个只有鸟和飞机的字数据集
label_map = {0: 0, 2: 1} # 0: 鸟, 1: 飞机
class_names = ['airplane', 'bird']
cifar2 = [(img, label_map[label]) for img, label in transformed_cifar10 if label in [0, 2]]
cifar2_val = [(img, label_map[label]) for img, label in transformed_cifar10_val if label in [0, 2]]
# mini-batch
train_loader = torch.utils.data.DataLoader(cifar2, batch_size = 64, shuffle = True)
val_loader = torch.utils.data.DataLoader(cifar2_val, batch_size = 64, shuffle = False)
2.3.1. mini-batch 优势
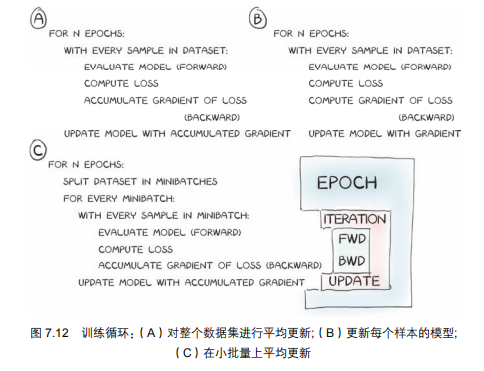
小批量梯度下降(Mini-batch SGD,如图7.12c所示)为什么比全量(7.12a)/单样本(7.12b)梯度下降更好 ?
核心是讲训练循环的优化思路,拆解如下:
2.3.1.1. 背景:训练循环的问题
之前的训练方式(全量梯度下降)有个缺点:如果数据集很大(比如10000张图),一次性评估所有样本再更新模型,计算量太大、内存扛不住。
2.3.1.2. 三种训练方式的对比
- 全量梯度下降:遍历整个数据集,累积所有样本的梯度后再更新模型 → 计算慢、内存压力大;
- 单样本梯度下降(SGD):每个样本单独计算梯度并更新模型 → 梯度波动大(单个样本的梯度方向可能和整体方向不一致),模型不稳定;
- 小批量梯度下降(Mini-batch):把数据集拆成“小批量”(比如每次取5个样本),遍历一个小批量后,用这几个样本的梯度平均来更新模型 → 是前两者的折中。
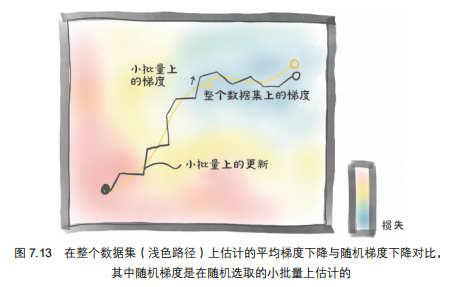
2.3.1.3. 小批量的优势
- 更稳定:小批量的梯度是“多个样本的平均”,比单样本梯度更接近“全量梯度”的方向,模型更新更平稳;
- 更高效:比全量梯度下降的计算/内存压力小,比单样本梯度下降的训练速度快;
- 避免局部最优:小批量的梯度会“随机偏离理想轨迹”,反而能帮助模型跳出局部最优。
用“小批量梯度下降”替代全量/单样本梯度下降,既解决了计算/内存问题,又让模型训练更稳定、高效。
2.3.1.4. 关键概念
- 小批量(Mini-batch):训练前要设置的固定大小(比如32、64),属于“超参数”(不是模型本身的参数)。
2.3.2. 如何实现mini-batch
在pytorch中,我们可以使用DataLoader来实现mini-batch。
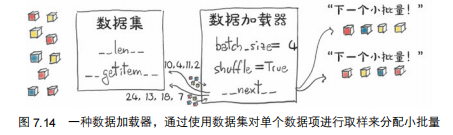
DataLoader类能够打乱和组织数据。他的构造函数接收一个数据集对象作为输入,以及batch_size和shuffle参数。
- batch_size:每个小批量的样本数量(比如32、64);
- shuffle:是否在每个epoch开始前打乱数据(一般设为True)。
Dataloader可以被for循环遍历,每次返回一个小批量的样本和标签。
例如:
for batch in train_loader:
imgs, labels = batch
# 训练模型
...
3. 搭建全连接模型
全连接网络形如:
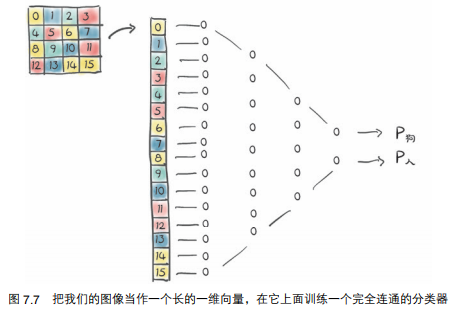
# 搭建一个全链接网络
import torch
import torch.nn as nn
import torch.optim as optim
# -----------------------------------------------------------------------
# 定义模型
n_out = 2
seq_model = nn.Sequential(
nn.Linear(3 * 32 * 32, 512), # 输入特征数为3*32*32 = 3072,输出特征数为512
nn.Tanh(),
nn.Linear(512, n_out), # 输入特征数为512,输出特征数为2
nn.LogSoftmax(dim = 1) # <- 对第1维应用softmax操作 (B x n, 第B个图像,每个类别(共n个)的概率)
)
learning_rate = 1e-2
optimizer = optim.SGD(seq_model.parameters(), lr = learning_rate)
loss_fn = nn.NLLLoss() # <- 分类工作使用负对数似然损失函数NLLLoss,而不是MSELoss
# -----------------------------------------------------------------------
# 测试模型
img, _ = cifar2[0]
plt.imshow(img.permute(1, 2, 0))
plt.show()
img_batch = img.view(-1).unsqueeze(0) # view(-1)将img展平 (3, 32, 32) -> (3072,); unsqueeze -> (1, 3072)
out = seq_model(img_batch)
print(out) # tensor([[0.4481, 0.5519]], grad_fn=<SoftmaxBackward0>)
关于损失的选择
3.1. 损失的选择
分类任务为什么不用 MSE 损失,而用负对数似然(NLL)损失?
- 核心是 “让损失函数更适配分类任务的目标”
3.1.1. 分类任务的核心目标
分类任务不是“精确预测概率值”,而是“让正确类别的概率高于其他类别”(比如识别“飞机”时,只要“飞机”的概率>“鸟”的概率即可,不用追求“飞机”的概率=1)。
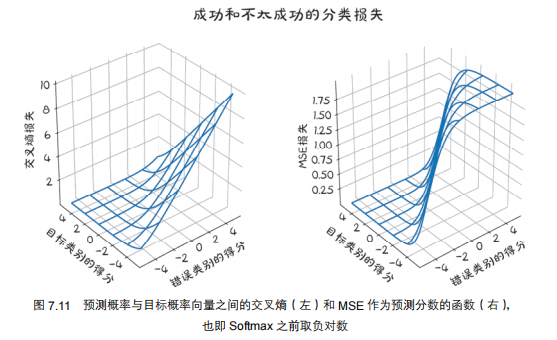
3.1.2. 为什么MSE不适合分类?
MSE(均方误差)是用来“回归(预测连续值)”的,用在分类上有2个问题:
- 梯度饱和:当预测概率已经接近1(正确类别)或0(错误类别)时,MSE的梯度会变得很小,模型很难继续优化;
- 惩罚过度:MSE会惩罚“概率不够精确”(比如正确类别概率是0.9,MSE会因为没到1而惩罚),但分类任务不需要这么精确。
3.1.3. 负对数似然(NLL)损失:分类的专属损失
NLL的核心是“惩罚‘正确类别概率低’的情况”,公式是:
(\(\text{out}[j]\)是正确类别的预测概率)
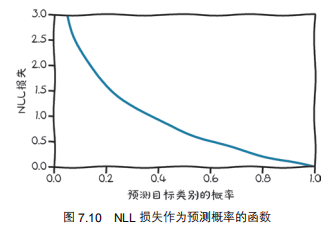
NLL的特点(对应图7.10):
- 当正确类别概率很低(比如0.1):\(\log(0.1)\)是负数,加负号后损失会很大(惩罚强);
- 当正确类别概率≥0.5:\(\log\)的下降速度变慢,损失不会过度惩罚“概率不够完美”的情况。
3.1.4. PyTorch中的实际用法(解决数值不稳定)
直接计算\(\log(\text{Softmax})\)会有“概率接近0时\(\log\)无穷大”的问题,所以PyTorch用LogSoftmax+NLLLoss的组合:
- 模型输出层用
LogSoftmax:直接输出“概率的对数”,避免数值溢出; - 损失函数用
NLLLoss:接收LogSoftmax的输出,计算负对数似然。
代码示例:
# 模型输出层加LogSoftmax
model = nn.Sequential(
...
nn.LogSoftmax(dim=1) # 输出“概率的对数”
)
# 实例化NLL损失
loss_fn = nn.NLLLoss()
# 计算损失:输入是LogSoftmax的输出+标签
loss = loss_fn(out, label)
3.1.5. 交叉熵损失:LogSoftmax+NLLLoss的组合
实际中更常用的是交叉熵损失(CrossEntropyLoss),它等价于LogSoftmax + NLLLoss,是分类任务的标准损失。
代码示例:
# 搭建一个全连接网络
## 定义模型
n_out = 2
model = nn.Sequential(
nn.Linear(3 * 32 * 32, 512), # 输入特征数为3*32*32 = 3072,输出特征数为512
nn.Tanh(),
nn.Linear(512, n_out), # 输入特征数为512,输出特征数为2
# nn.LogSoftmax(dim = 1) # 对第1维应用softmax操作 (B x n, 第B个图像,每个类别(共n个)的概率)
)
# ...
# loss_fn = nn.NLLLoss() # 分类工作使用负对数似然损失函数NLLLoss,而不是MSELoss
loss_fn = nn.CrossEntropyLoss() # 分类工作使用交叉熵损失函数CrossEntropyLoss,而不是MSELoss
3.1.6. 总结
分类任务用NLL(或交叉熵)而不用MSE的原因:
- NLL更贴合“让正确类别概率更高”的分类目标;
- 避免MSE的梯度饱和、过度惩罚问题;
- 结合
LogSoftmax解决数值不稳定。
3.2. 训练模型
# -----------------------------------------------------------------------
## 训练分类器
n_epochs = 100
for epoch in range(n_epochs):
for img, label in train_loader: # <- 从train_loader中取出一个batch的图像和标签
batch_size = img.shape[0] # <- img.shape = (64, 3, 32, 32)
out = model(img.view(batch_size, -1)) # <- 将图像展平为 (64, 3072)
loss = loss_fn(out, label)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 10 == 0:
print(f"Epoch: {epoch}, Loss: {float(loss)}")
实验结果如下:
Epoch: 0, Loss: 0.6439802646636963
Epoch: 10, Loss: 0.3364253044128418
Epoch: 20, Loss: 0.2660796046257019
Epoch: 30, Loss: 0.3763981759548187
Epoch: 40, Loss: 0.24415557086467743
Epoch: 50, Loss: 0.1775331050157547
Epoch: 60, Loss: 0.03261692821979523
Epoch: 70, Loss: 0.04219042509794235
Epoch: 80, Loss: 0.020144721493124962
Epoch: 90, Loss: 0.02759580872952938
3.3. 验证模型
# -----------------------------------------------------------------------
## 验证分类器
n_correct = 0
n_total = 0
with torch.no_grad():
for img, label in val_loader:
batch_size = img.shape[0]
out = model(img.view(batch_size, -1))
_, predicted = torch.max(out, dim = 1)
n_correct += int((predicted == label).sum())
n_total += batch_size
print(f"Accuracy: {n_correct / n_total}")
实验结果如下:
Accuracy: 0.813
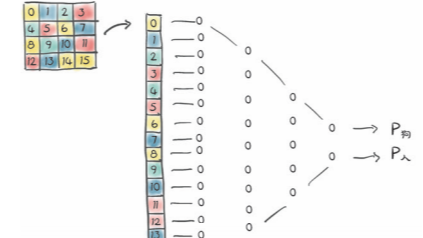
4. 全连接网络的局限性
我们检查这个简单的全连接网络的参数数量:
# -----------------------------------------------------------------------、
# 模型
n_out = 2
model = nn.Sequential(
nn.Linear(3 * 32 * 32, 512), # 输入特征数为3*32*32 = 3072,输出特征数为512
nn.Tanh(),
nn.Linear(512, n_out), # 输入特征数为512,输出特征数为2
nn.LogSoftmax(dim = 1) # 对第1维应用softmax操作 (B x n, 第B个图像,每个类别(共n个)的概率)
)
learning_rate = 1e-2
optimizer = optim.SGD(model.parameters(), lr = learning_rate)
loss_fn = nn.NLLLoss() # 分类工作使用负对数似然损失函数NLLLoss,而不是MSELoss
# -----------------------------------------------------------------------
# 检查参数数量
numlist = [p.numel()
for p in model.parameters()
if p.requires_grad]
print(sum(numlist), numlist) # 1574402 [1572864, 512, 1024, 2]
exit()
这个简单的模型,参数居然有150万,太大啦,导致模型过拟合!
而且,全连接网络只认识像素的固定位置,而不认识物体的形状,如图所示。
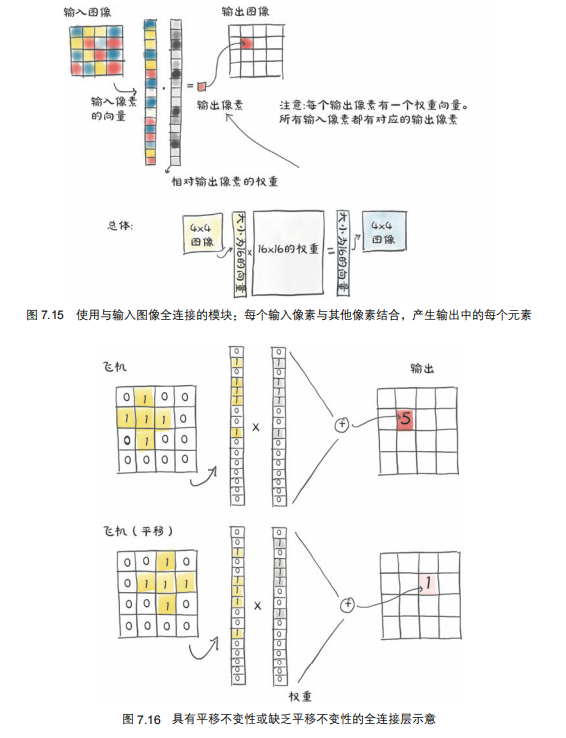
因此,下一篇文章,引出卷积神经网络。
5. 本文完整代码
点击查看完整代码
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets
from torchvision.transforms import ToTensor # PIL (0~255) -> Tensor (0.0~1.0)
from torchvision.transforms import Normalize # 归一化
from torchvision.transforms import Compose # 组合多个变换
# -----------------------------------------------------------------------
# 加载数据
data_path = './data/CIFAR-10/'
transform = Compose([ToTensor(), Normalize((0.4914, 0.4822, 0.4465), (0.2470, 0.2435, 0.2616))])
transformed_cifar10 = datasets.CIFAR10(data_path, train = True, download = True, transform = transform)
transformed_cifar10_val = datasets.CIFAR10(data_path, train = False, download = True, transform = transform)
# -----------------------------------------------------------------------
# 一个只有鸟和飞机的字数据集
label_map = {0: 0, 2: 1} # 0: 鸟, 1: 飞机
class_names = ['airplane', 'bird']
cifar2 = [(img, label_map[label]) for img, label in transformed_cifar10 if label in [0, 2]]
cifar2_val = [(img, label_map[label]) for img, label in transformed_cifar10_val if label in [0, 2]]
train_loader = torch.utils.data.DataLoader(cifar2, batch_size = 64, shuffle = True)
val_loader = torch.utils.data.DataLoader(cifar2_val, batch_size = 64, shuffle = False)
# -----------------------------------------------------------------------
# 搭建一个全连接网络
## 定义模型
n_out = 2
model = nn.Sequential(
nn.Linear(3 * 32 * 32, 512), # 输入特征数为3*32*32 = 3072,输出特征数为512
nn.Tanh(),
nn.Linear(512, n_out), # 输入特征数为512,输出特征数为2
nn.LogSoftmax(dim = 1) # 对第1维应用softmax操作 (B x n, 第B个图像,每个类别(共n个)的概率)
)
learning_rate = 1e-2
optimizer = optim.SGD(model.parameters(), lr = learning_rate)
loss_fn = nn.NLLLoss() # 分类工作使用负对数似然损失函数NLLLoss,而不是MSELoss
# -----------------------------------------------------------------------
## 训练分类器
n_epochs = 100
for epoch in range(n_epochs):
for img, label in train_loader:
batch_size = img.shape[0]
out = model(img.view(batch_size, -1))
loss = loss_fn(out, label)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 10 == 0:
print(f"Epoch: {epoch}, Loss: {float(loss)}")
# -----------------------------------------------------------------------
## 验证分类器
n_correct = 0
n_total = 0
with torch.no_grad():
for img, label in val_loader:
batch_size = img.shape[0]
out = model(img.view(batch_size, -1))
_, predicted = torch.max(out, dim = 1)
n_correct += int((predicted == label).sum())
n_total += batch_size
print(f"Accuracy: {n_correct / n_total}")


 本文以区分CIFAR-10数据集中的鸟和飞机图像为实战目标,通过PyTorch完整演示深度学习流程。首先加载数据并预处理:将PIL图像转为张量,计算通道均值与标准差进行标准化,筛选出目标类别构建简化数据集;随后设计输入层(3072)→隐藏层(512)→输出层(2)的全连接网络,使用小批量梯度下降优化,选择适合分类任务的NLL损失函数。经过100轮训练,验证集准确率达81.3%。但该模型存在参数冗余(150万+参数易过拟合)、对图像空间结构不敏感等局限,因此下一篇将引入卷积神经网络解决这些问题。
本文以区分CIFAR-10数据集中的鸟和飞机图像为实战目标,通过PyTorch完整演示深度学习流程。首先加载数据并预处理:将PIL图像转为张量,计算通道均值与标准差进行标准化,筛选出目标类别构建简化数据集;随后设计输入层(3072)→隐藏层(512)→输出层(2)的全连接网络,使用小批量梯度下降优化,选择适合分类任务的NLL损失函数。经过100轮训练,验证集准确率达81.3%。但该模型存在参数冗余(150万+参数易过拟合)、对图像空间结构不敏感等局限,因此下一篇将引入卷积神经网络解决这些问题。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号