JOISC部分题解

JOISC部分题解

懒得全部写完了，选了一些自己觉得海星的题更。
题目名称是 loj 上的。

---

2014

巴士走读

建反图后，将询问按照\(L\)从小到大排、，边按照\(Y\)从小到大排序后跑 dij，对于每个点维护一个单调指针，每次把能加入图中的边加入，发现如果一条边在先前已经加入这个图中我们没必要继续加，这样子的话复杂度是\(O(m\log n+Q)\)的。
code

有趣的家庭菜园

考虑由高到低加入这些草，那么每次加入一颗草时我们需要考虑的就是这颗草是放在所有已放入的草的右侧还是左侧，每次加入的代价就是逆序对数目，选代价少的一遍加入即可，注意相同高度的要一起加进去。
code

交朋友

首先对于一个点连出去的所有出边，他们所对应的点一定是可以最后形成一个团的。
我们首先把这些点可以形成团的点给并起来，用并查集维护，但是连好后可能还会有新的团出现。
我们把所有所在团大小大于\(1\)的点给拿出来进行 bfs，如果某个点被访问到那么就可以继续合并，不难发现这样做可以把最后的连通情况维护出来。
code

邮戳拉力赛

使用一次\(U\to E\)必然会在前面的站点使用一次\(D\to V\)，我们可以把前者看作)，后者看作(，设\(f_{i,j}\)表示前\(i\)个站点目前有\(j\)个(的最小代价，分类讨论一下转移即可。
code

稻草人

非常经典的模型。
考虑 CDQ 分治算左边对右边的贡献，我们保证左边的横坐标小于右边，将两边分别按照纵坐标从小到大排序，枚举右边的某个纵坐标然后单调指针加入左边的纵坐标同时维护出左边关于横坐标从栈底到栈顶递减的单调栈，因为右边对自己也有影响所以也要维护出右边的单调栈求出目前枚举的点左边比他矮的最高高度，最后在左边的单调栈上二分出这个点能匹配的在栈中最浅的点的位置就是左边对右边某个点的贡献（可匹配的点一定是段后缀）。
复杂度\(O(n\log ^2n)\)。
code

两个人的星座

两个三角形相离一定会存在两条内公切线。
那么可以考虑枚举公切线计算出有多少对三角形以该线为公切线之一，把所有线的答案加起来除以二就是最终答案。
直接枚举两个点作为公切线比较浪费时间，考虑枚举一个点然后把其他所有点以该点为原点极角排序，再按极角序枚举另外那个点，分别维护出这条直线两侧每种颜色出现的点数可以计算。
code

2015

Keys

把所有\(S,T\)拿出来然后按照时间排序，对于相邻的两个时间点，如果是同一个人的\(S,T\)，如果这个人有钥匙，那么可以关上的贡献就是\(T-S\)，否则分类讨论一下：
\(S,S:\)前面的人带钥匙有时间间隔的贡献
\(T,S:\)直接给答案加上时间间隔的贡献
\(T,T:\)后面的人带钥匙有时间间隔的贡献
\(S,T:\)两人同时带钥匙有时间间隔的贡献
对于最后一种情况，可以看出一定形成了许多的链，设\(f_{i,j,0/1}\)表示目前在链上第\(i\)个点，目前已经给了\(j\)个人钥匙，这个人选没选的最长时间，可以结合上面的几种情况dp。
code

Card Game Is Great Fun

分析一下性质发现如果选第\(1\)张牌的话第\(1\)张牌的位置变为原来的第\(2\)张牌，第\(2\)张牌的位置变为原来的第\(3\)张牌，第\(3\)张牌的位置点数加\(1\)。
设\(f_{i,j,k}\)表示第\(3\)张牌是\(i\)，第\(1\)张牌是\(j\)，第\(2\)张牌是\(k\)，上次选出的牌是\(i-1\)的最大贡献，设\(g_{i,j,k}\)表示第\(3\)张牌是\(i\)，第\(1\)张牌是\(j\)，第\(2\)张牌是\(i-1\)，上次选出的牌是\(k\)的最大贡献。
然后互相转移即可。
code

upd on 2021.1.20：
考试的时候碰到了这道题，然后当我满脸惊喜的时候，翻到下面的数据范围，发现了 \(N\leq 1919\)，然后人就傻了，所以更新一下
考虑上述的 dp ，发现 \(f\) 的状态表示的是形如 \(j,k,i,i+1,i+2...\) 的栈， \(g\) 的状态表示的是形如 \(j,i,i+1,i+2...\) 的栈，如果我们知道某个状态可不可达我们可以直接将一个状态的贡献算出来然后计算答案，所以 \(f,g\) 实际上可以开成 \(\text{bool}\) 类型。
考虑每一次 dp 的转移，有：

\[\begin{cases} f_{i,j,k}\to f_{i+1,j,k}\\ g_{i,j,k}\to f_{i+1,j,i}\\ f_{i,j,k}\to g_{i+1,k,j}\\ g_{i,j,k}\to g_{i+1,i-1,j} \end{cases} \]

接下来为了方便转移，我们将 \(f\) 中 \(j,k\) 的顺序 swap，并且记录分别 \(\text{bitset}\) 表示一个牌后边能跟什么牌，一个牌前面能跟什么牌。
分别考虑对转移的优化（注意下面的 \(i,j\) 是调换之前的）：
\(f_{i,j,k}\to f_{i+1,j,k}:\) 条件是 \(i-1\) 后可以直接跟 \(i\)，直接继承。
\(g_{i,j,k}\to f_{i+1,j,k}:\) 条件是 \(k\) 后可以直接跟 \(i\)，枚举 \(j\) 用先前预处理的 \(\text{bitset}\) 判断。
\(f_{i,j,k}\to g_{i+1,k,j}:\) 条件是 \(i-1\) 后可以直接跟 \(j\)，枚举 \(j\) 后和之前预处理的 \(\text{bitset}\) 进行 \(\text{AND}\) 操作即可。
\(f_{i,j,k}\to g_{i+1,i-1,j}:\) 条件是 \(k\) 后可以直接跟 \(j\)，和第二种情况一样的枚举 \(j\) 后 \(\text{bitset}\) 判断。

最后还有一个问题就是算答案，记后缀和为 \(suf_i\)。
对于所有的 \(g\)，答案是容易处理的，因为与 \(k\) 无关，直接用 \(\text{bitset}\) 判断有无 \(k\) 用后缀和计算。然后是 \(f\)，由于我们先前交换过 \(j,k\) ，所以考虑首先固定住 \(k\)，然后因为答案的式子可以表示为 \(suf_1-suf_i-V_k-V_j\)，所以对于某一个\(j\)，\(i\)肯定越大越好，我们可以从大到小枚举\(i\)，然后每次维护出新出现的 \(j\)，并更新答案。可以看出上述过程在正确的时间复杂度求出了 \(f,g\) 所表示状态的最大值。

所以总复杂度\(O(\frac{N^3}{\omega})\)（这题因为当时空间 512 所以用指针卡了波常）。
code

Inheritance

将边权从大到小排序，从边权最大的点开始扫描，扫描到某个点时，边权比他小的边是不会对它的答案造成影响的。
对于某条边，如果它在\(k\)时刻合并，说明前面的\(k-1\)时刻这两个点已经在一个联通块中了，这启发我们维护\(K\)个并查集，每个并查集\(i\)维护时刻\(i\sim K\)的联通块情况，这样每次询问时二分出第一个可以加入的时刻即可。
因为二分的性质，所以每次只需在当前答案的并查集加入那条边就可以了（写的时候sb了，把整个后缀都更新了一遍，但是因为有效的更新只有NK遍，所以还是可以通过）。
code

防壁

所有连续的位置递增或者递减的点只有两端点有用，所以只需要留下这些点，这些点会分为左和右两个部分，同时对于这些点中相邻的两点，我们将其称作一“段”，一段的长度即为两点的坐标之差。
对于某个防壁，如果它的左端点挨在了左部分或者右端点挨在了右部分，那么长度小于等于它的段就没有意义了，这个防壁不会进行移动，用\(set\)维护出所有的段，那么我们最后的答案就是 其中的元素长度之和\(-\)个数$\times $当前长度。
将所有防壁按照长度从小到大排序，依次加入，如果目前有的段长度小于等于当前防壁的长度，将该段删除，并加入新的段，因为我们要保证左右端点挨紧，所以可以直接模拟防壁在最开头两个段的移动过程。
具体实现细节详见代码。
code

AAQQZ

不想写，咕咕咕

2016

棋盘游戏

先把\(0\)的情况判掉，即四个角落没有填上，或者第一、三列出现了连续的长度\(\geq 2\)的空位。
那么中间的棋子就把整个棋盘划分为了很多个联通块，把每个联通块的答案卷起来就是答案。
对于中间的某个空位，可以通过上下或是左右填上，而且对于某个联通块的方案数，和当前所填的时间有关，所以可以以此设计一个 dp 状态：\(f_{i,j,0/1}\)表示当前联通块的前\(i\)列，在只考虑前\(i\)列的操作的\(j\)时刻填上，满足上下/左右比它先填完的方案数，为了避免算重，我们把上下左右均比他先填的方案算到\(0\)中。
记当前列第一、三行的空位有\(cnt\)个，前\(i\)个位置共\(siz\)个空位考虑转移

\[f_{i,j,0}= \begin{aligned} \begin{cases} \sum f_{i-1,k,0}\times {j-1\choose cnt}cnt!\\ \sum f_{i-1,k,1}\times {j-1\choose cnt}cnt!,\ \ k+cnt\geq j \end{cases} \end{aligned} \\ f_{i,j,1}= \begin{aligned} \begin{cases} \sum_{k<j} f_{i-1,k,0} \times cnt!\times({siz-1\choose cnt}-{j-1\choose cnt}),k<j-1\\ \sum_{k<j} f_{i-1,k,0} \times cnt!\times {siz-j\choose cnt},k=j-1 \end{cases} \end{aligned} \]

前缀和优化下就做完了。
code

三明治

\(O(n^4)\)直接枚举某个位置然后记搜求出答案。
\(O(n^3)\)的话，可以发现删除某个位置必须删除其左边到右边的所有位置，可以对于某一行从左往右删一下，再从右往左删一下，就是\(O(n^3)\)的了。
code

女装大佬

把男的看作\(-1\)，女的看作\(1\)，统计后缀和，如果某个后缀和\(\leq -2\)那么说明不合法，也就是最大前缀和小于等于总和\(+1\)（总和必须\(\geq 0\)），统计出前缀和后和总和算一下就好了。
code

回转寿司

维护的东西十分奇怪，考虑分块。
那么我们如果想分块快速查询的话需要什么：快速求出经过一个块后的答案、通过下放标记暴力求出散块的答案。
前者可以每块维护大根堆，后者的下放标记操作相当于很多修改一起进入，显然每个位置会选出最小的那个，搞个小根堆维护下就是了。
code

最差记者 2

考虑一个费用流模型，把\(B,D\)按照时间从小到大排序，那么对于某个\(D\)，他向\(B\)的一段前缀连边，如果国籍相同则费用为\(0\)，否则为\(1\)（容量均为\(1\)）。
对于这种前缀型的匹配我们考虑按照可选集合的大小从小往大选，如果当前点可以选择不增加贡献的话就选择不增加否则只能增加，至于如何维护可不可以增加贡献，就是考虑选择当前点后图中是否还存在完美匹配。
判断是否存在完美匹配考虑 Hall 定理，给\(D\)前缀\(+1\)，\(B\)前缀\(-1\)，修改时变为\(D:-1,B:+1\)，用线段树维护前缀修改、全局求最小值可以判断。
code

2017

感觉难度瞬间起飞

开荒者

首先发现最终操作结果与操作顺序无关。
考虑枚举往南和往北的吹风次数\(s,n\)，那么对于某一行的\(m\)个坐标上的草\(\{a_m\}\)（单增），所需西风数\(w\)以及所需东风数\(e\)至少为\(a_1-1\)以及\(C-a_m\)，所需总次数至少为\(\max_{i=2}^m a_i-a_{i-1}\)。
现在分别枚举\(s,n\)，复杂度\(O(N^3)\)，再算答案一次\(O(N^2)\)，就是\(O(N^5)\)，复杂度不能接受，考虑优化。
发现当\(n+s\)相同时，若没有边界限制，怎么吹草场最后的形状都是一样的，只需要拿长度为\(R\)的上下边界将一些区域“框住”，发现这就是一个滑动窗口的模型，直接拿单调队列维护上述的\(3\)个信息的\(\max\)，可以做到\(O(N)\)，乘上前面枚举的\(O(N^2)\)一共\(O(N^3)\)。
code

港口设施

不难发现如果两区间是相交关系而非嵌套关系，就证明这两个区间不能放在同一个栈中。
将不能放在联通块的区间连边，那么题目就是让我们求\(2^{形成联通块个数}\)（如果有联通块不是二分图答案为\(0\)）。
直接连边是\(O(n^2)\)的，考虑优化。
将所有区间按照左端点排序，按照右端点从小到大扫描，扫描时维护个线段树，线段树中间存储的信息是当前区间内是否有某个区间的左端点以及该区间的标记（标记是什么下面再说）。
扫描到这个区间时，我们先在相应的线段树上区间打上这个区间的标记，然后把这个区间的左端点从线段树上删除，删除时访问左端点遍历到的每个节点的标记，用并查集维护这两个标记的区间不能合并到一起，需要注意的是在第一步打标记时我们需要判断这个区间内是否仍然存在左端点，不存在就没有必要也不能继续递归，因为如果碰到其他需要合并的标记就证明当前和之前的两个标记碰上了同一个左端点，用并查集维护这两个点必须在一起（同色）。
最后如果有一个点自相矛盾了就是\(0\)，否则就利用并查集上的连通信息输出答案，复杂度\(O(n\log n\alpha(n))\)。
code

烟花棒

考虑二分答案。
显然所有的人肯定会以最快速度朝着目前场上着火的人跑，着火的人也以会以最快的速度跑。
当一个没火的人与一个着火的人相遇后，如果他俩继续跑同向的话，可以发现没火的人一定是在着火的人燃尽的瞬间被点燃，又发现如果两个人相遇后继续方向相反跑的话可以被同向跑的方案取代，所以可以认为一次相遇就是给目前场上着火的人续了\(T\)的单位时间，而且任意时刻场上都只出现了一个着火的人。

注意到着火的人可以将整个序列分为左右两部分，如果向其中一边跑另一边和这个人的相对位置还是不变的，那么我们可以把每个人看成一个二元组\((a,b)\)，表示选这个人就会先失掉\(a\)再加上\(b\)。

接下来考虑一个贪心的过程，我们可以将左部的后缀和右部的前缀分为若干个极小的段，每一段吃掉之后自身的血量都会增加（没有就直接进入下一个过程），那么我们一定会选择开头掉血少的段吃掉最优。
这一个过程就是把上面可以回血的吃掉之后了，我们把过程逆过来，就变为先减去\(b\)再加上\(a\)，两边的连续段也reverse了，还需要保证过程中血量不为负，显然可以应用上面的贪心思路解决下面的问题。

复杂度\(O(n\log n)\)
code

门票安排

这里写了

火车旅行

对于一个\(a\to b\)的路线，它所到的高度一定是先升高后降低，等价于走出两条升高的路线。
又有在换乘次数一定的情况下，升高的路线所能走到的一定是段区间，所以我们可以判断从\(a,b\)分别走出一定换乘的次数，他们的可达区间如果可以相交就证明当前长度可行。
然后就是怎么确定换乘次数可以到哪，设\(L_{i,j}\)表示从\(i\)向左换\(2^j\)下最多走到哪，设\(R_{i,j}\)表示从\(i\)向右换\(2^j\)下最多走到哪，转移的话这两个倍增数组可以互相转移，每次查询也大同小异。
code

长途巴士

如果确定要把一些乘客弄下车，那么我们一定会尽早弄下去。

将乘客按照\(D_i\)升序排序，对于某个服务站\(j\)，如果\(S_j\bmod T\in(D_i,D_{i+1})\)，我们可以在司机有水喝的情况下让\([x,i],x\in [1,i]\)的乘客下车。

考虑 dp ，设\(f_i\)表示前\(i\)个乘客最小化费是多少，那么有转移：

\[\begin{aligned} \begin{cases} f_i = f_{i-1} + \lceil \frac{X - D_i}{T} \rceil \times W\\ f_i = \min\limits_{0 \leq j < i} f_j + (i - j) \times W \times cnt + \sum\limits_{k = j + 1}^i C_k \end{cases} \end{aligned} \]

第一种转移就是保留当前这个人；第二个转移是算出把\([j+1,i]\)的人弄下去的代价，其中\(cnt\)是需要开销的最少次数即\(\min\limits_{S_k\ \bmod\ T \in (D_i , D_{i+1})}\lfloor \frac{S_k}{T} \rfloor\)，这个转移需要保证\((D_i,D_{i+1})\)之间有服务站，因为任意时候选择的区间肯定无交所以是对的。

把\(\sum C\)拆成前缀和然后斜率优化单调栈维护凸壳即可。
code

幽深府邸

对于一个房间只有左右离他最近的钥匙有用，而如果一个房间可以到达另外一个房间那么可达的那个房间的可达范围可以给可达这个房间的房间继承。
对于每个房间记忆化搜索一下即可。
code

绑架 2

直接记忆化搜索，总状态量是\(O(n)\)的有没有人教教我我不会证啊啊啊。
线段树/倍增优化找拐点即可。
code

Dragon 2

这类总量不变选两个集合出来的题如果遍历小的那边然后记忆化复杂度用根号分析一下容易得到遍历次数是\(O(n\sqrt n)\)的。

考虑攻击龙\(A\)和被攻击龙\(B\)，\(A\)在如下范围内被攻击是能打到线的：

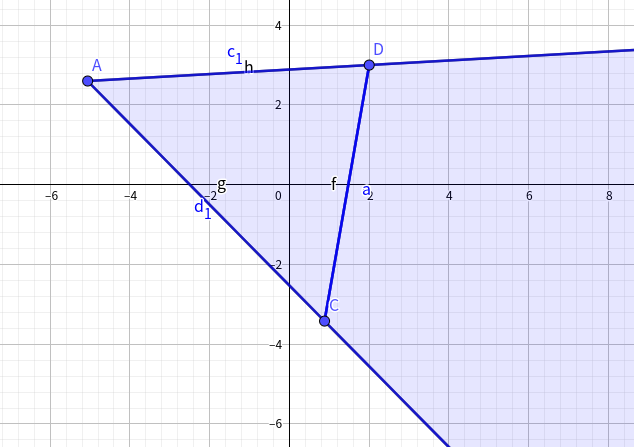
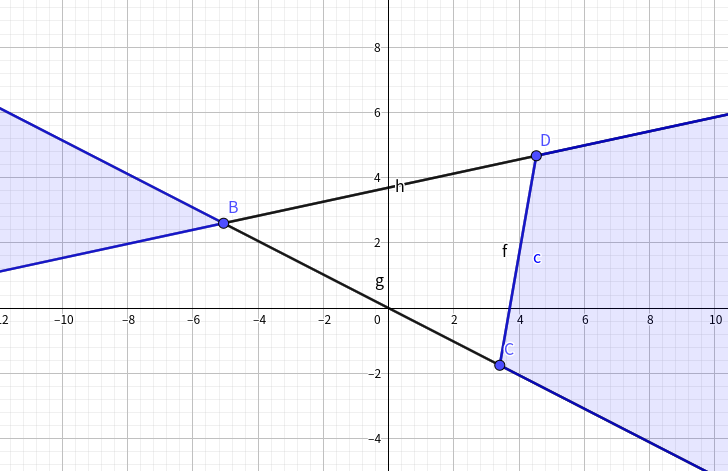
将所有点按照以两个端点为原点的极角搞个二维坐标出来，把龙分为线段左右两边再分类讨论一下上述情况二维数点即可，复杂度\(O(n\sqrt n\log n)\)。
code