算法技巧_二叉树

算法技巧(二叉树)

目录

两种解题思路

  1. 遍历一遍树是否可以解决问题 如果可以，用一个 traverse 函数配合外部变量来实现。
  2. 分解问题 是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值。

一旦你发现题目和子树有关，那大概率要给函数设置合理的定义和返回值，在后序位置写代码了

  1. 无论使用哪一种思维模式，你都要明白二叉树的每一个节点需要做什么，需要在什么时候（前中后序）做

二叉树特征

  1. 满二叉树
    1. 满二叉树有个优势，就是它的节点个数很好算。假设深度为 h，那么总节点数就是 2^h - 1
  2. 完全二叉树
    1. 二叉树的每一层的节点都紧凑靠左排列，且除了最后一层，其他每层都必须是满
  3. 平衡二叉树
    1. 平衡二叉树（Balanced Binary Tree）是一种特殊的二叉树，它的「每个节点」的左右子树的高度差不超过 1。要注意是每个节点，而不仅仅是根节点。
  4. 二叉搜索树
    1. 对于树中的每个节点，其左子树的每个节点的值都要小于这个节点的值，右子树的每个节点的值都要大于这个节点的值。你可以简单记为「左小右大」
  5. 如何实现一个二叉树？
    1. 使用数组。
    2. 根据函数堆栈生成。
    3. 哈希表
    4. 自己定义 手动组装。
  6. 遍历二叉树的方式？
    1. DFS
      1. 递归
    2. BFS
      1. 借助队列 先进先出。
  7. DFS BFS 常用于解决什么问题？
    1. DFS BFS 都可以解决树的高度问题。
      1. DFS 需要遍历完所有树，每个递归就是一条线，全局维护一个变量 比较这个值 来记录是否是最小高度。
      2. BFS 需要借助队列入队 出队 动作，先将跟节点入队，然后出队；如果碰到自己的左右孩子节点为空，则终止；否则 左右孩子入队，树高加1；
      3. BFS 和DFS 算法复杂度 取决于树的质量 如何不是平衡二叉树 贼退化成链表 O(N)；通常BFS是O(logN)；常用于计算树高；DFS 则被用于查找所有路径。
  8. 多叉树
    1. 因为是多个节点 则没有中序；只需要有前后序。
    2. DFS
      1. 递归节点的所有子节点。
    3. BFS
      1. 队列入队所有子节点。
  9. 二叉树的搜索及其应用
    1. JAVA中的TreeMap;可以维护顺序,底层本质是一个二叉搜索树。
    2. 红黑树(自平衡的二叉树) 在插入和删除的时候增加旋转，让其在搜索的时候是始终保持O(logN)。
    3. Trie/字典树/前缀树
      1. 是一种针对字符串进行特殊优化的数据结构。
  10. 二叉堆
    1. 二叉树上的任意节点的值，都必须大于等于（或小于等于）其左右子树所有节点的值。如果是大于等于，我们称之为「大顶堆」，如果是小于等于，我们称之为「小顶堆」。
    2. 主要操作
      1. 下沉sink和上浮swim
    3. 主要数据结构
      1. 优先级队列
      2. 堆排序
  11. 跳表
    1. 时间复杂度 O(logN)
    2. 维护多层索引在每层索引中移动的次数不会超过 2 次（因为上层索引区间在下一层被分为两半）。
  12. 十大排序算法指标
    1. 关键指标
      1. 时间复杂度
      2. 空间复杂度
      3. 稳定性排序
        1. 排序之后它们相对位置没有发生改变，则称之为稳定排序。反之为不稳定排序。
      4. 原地排序就是指排序过程中不需要额外的辅助空间，只需要常数级别的额外空间，直接操作原数组进行排序。
  13. 十大排序算法
    1. 选择排序

最简单的遍历二叉树代码

    List<Integer> res = new LinkedList<>();
    public void traverse(TreeNode root){
        if(root == null){
            return;
        }
        //前序位置
        res.add(root.val)
        traverse(root.left)
        traverse(root.right)
        //后序位置
    }

遍历二叉树的方式

  1. 前序 （根左右）
  2. 中序 （左根右）
  3. 后序 （左右根）
  4. BFS （广度遍历搜索）
  5. DFS (深度遍历搜索)

前中后序遍历的区别以及各自场景

  1. 前序是自顶向下遍历的，后序是自底向上遍历的。前序位置的代码只能从函数参数中获取父节点传递来的数据
  2. 前序是刚刚进入节点的时刻，后序位置是即将离开节点的时刻。
  3. 后序位置代码不仅仅可以获取参数数据，还可以获取到子树通过函数返回值传递回来的数据

技巧

  1. 回溯
    • 属于遍历的思路，它的关注点在节点间的「树枝」
    • 它的着眼点永远是在节点之间移动的过程，类比到二叉树上就是「树枝」。
  2. 动态规划
    • 动态规划算法属于分解问题的思路，它的关注点在整棵「子树」
    • 它的着眼点永远是结构相同的整个子问题，类比到二叉树上就是「子树」
  3. DFS
    • 属于遍历的思路，它的关注点在单个「节点」
    • 它的着眼点永远是在单一的节点上，类比到二叉树上就是处理每个「节点」

典型问题

  1. 如果把根节点看做第一层，如何打印出第一个节点所在的层数？(遍历一遍树 前序位置打印层级)
  2. 如何打印出每个节点的左右子树各有多少节点？（分解问题 求出每个子树的节点 后序位置打印）

常见题目以及解题思路

  1. leetcode 二叉树的直径 求二叉树最长的直径
  • 解题思路：
    • 二叉树的长直径长度就是任意两个结点之间的路径长度 最长直径并不一定要求穿过根节点
    • 关键：每一条二叉树的直径长度 就是一个节点的左右子树的最大深度之和。
           class Solution {
       // 记录最大直径的长度
       int maxDiameter = 0;

       public int diameterOfBinaryTree(TreeNode root) {
           maxDepth(root);
           return maxDiameter;
       }

       int maxDepth(TreeNode root) {
           if (root == null) {
               return 0;
           }
           int leftMax = maxDepth(root.left);
           int rightMax = maxDepth(root.right);
           // 后序位置，顺便计算最大直径
           int myDiameter = leftMax + rightMax;
           maxDiameter = Math.max(maxDiameter, myDiameter);

           return 1 + Math.max(leftMax, rightMax);
       }
   }
  1. BFS 实现
  • 遍历实现
    // 输入一棵二叉树的根节点，层序遍历这棵二叉树
    void levelTraverse(TreeNode root) {
        if (root == null) return;
        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);

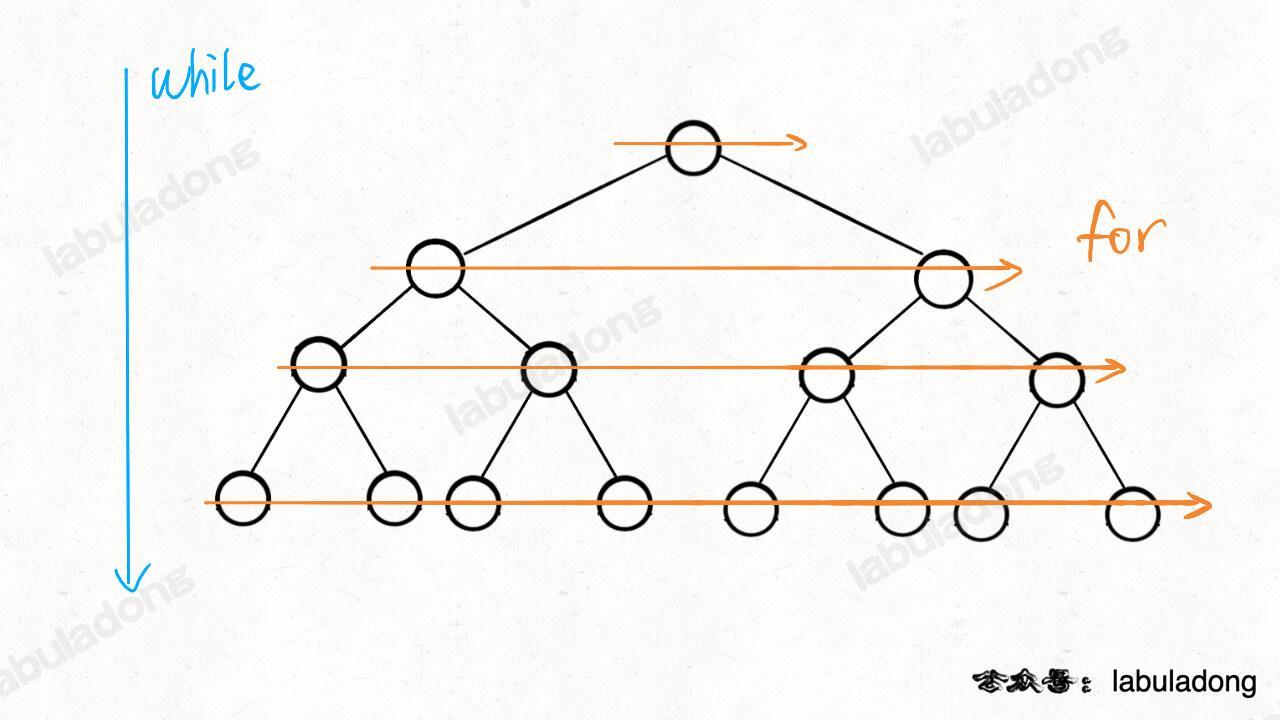
        // 从上到下遍历二叉树的每一层
        while (!q.isEmpty()) {
            int sz = q.size();
            // 从左到右遍历每一层的每个节点
            for (int i = 0; i < sz; i++) {
                TreeNode cur = q.poll();
                // 将下一层节点放入队列
                if (cur.left != null) {
                    q.offer(cur.left);
                }
                if (cur.right != null) {
                    q.offer(cur.right);
                }
            }
        }
    }
  • 递归解法
    class Solution {
        List<List<Integer>> res = new ArrayList<>();

        List<List<Integer>> levelTraverse(TreeNode root) {
            if (root == null) {
                return res;
            }
            // root 视为第 0 层
            traverse(root, 0);
            return res;
        }

        void traverse(TreeNode root, int depth) {
            if (root == null) {
                return;
            }
            // 前序位置，看看是否已经存储 depth 层的节点了
            if (res.size() <= depth) {
                // 第一次进入 depth 层
                res.add(new LinkedList<>());
            }
            // 前序位置，在 depth 层添加 root 节点的值
            res.get(depth).add(root.val);
            traverse(root.left, depth + 1);
            traverse(root.right, depth + 1);
        }
    }

img

posted @ 2024-04-12 16:00  贺艳峰  阅读(23)  评论(0)    收藏  举报