常见九大内排序算法实现(C语言)
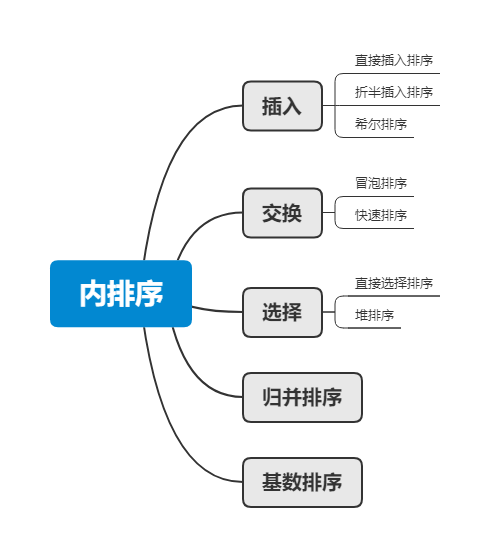
声明:部分动图是网上找的,因为前一版自己做的图太丑了,但保留了部分我认为有助于理解的静态图。
环境:
提示:附上头文件如下。
// hello.h
#include <stdio.h>
#include <malloc.h>
#define arr_len 8
void print_array(int arr[], int array_length) {
for (int i = 0; i < array_length; ++i) {
printf("%d ", arr[i]);
}
printf("\n");
}
1.直接插入排序
思想:
把待排序部分分为有序和无序两个部分,从无序部分取出元素直接插入到有序部分。通常把数组的第一个元素看作有序,后面所有看作无序。所以就有了遍历无序部分元素和插入到有序部分两个过程,遍历的时间复杂度是O(n),插入时要查找正确的插入位置,根据查找位置的方式又分为直接插入排序和折半插入排序。直接插入就是遍历有序部分,直到找到正确插入位置。
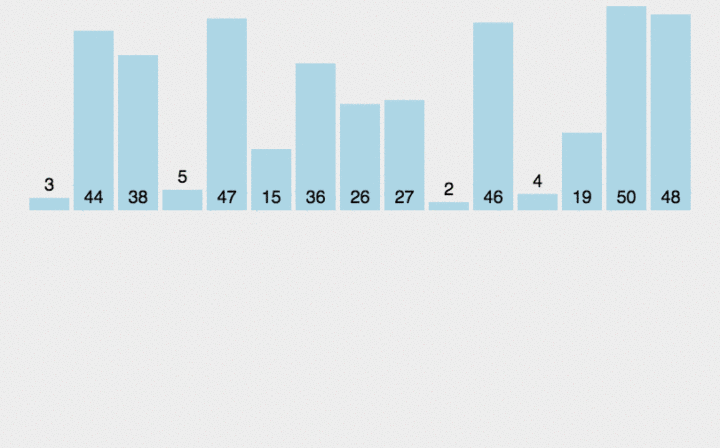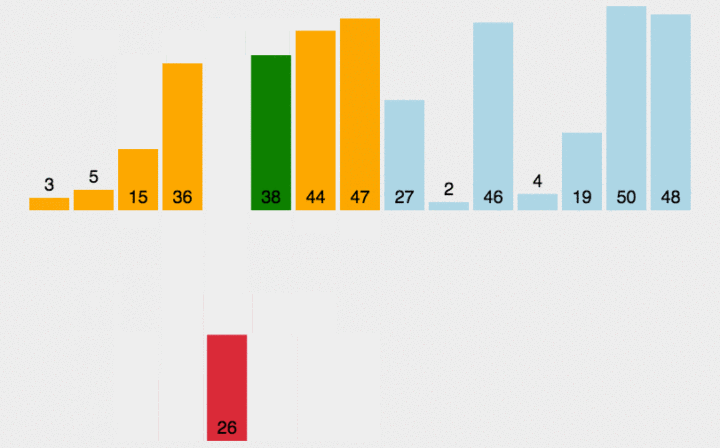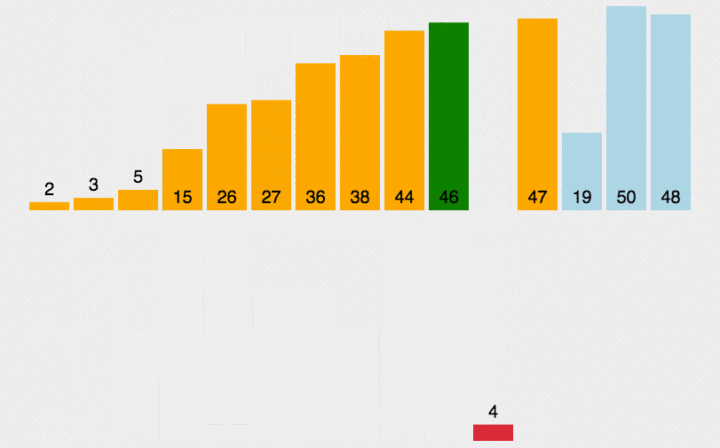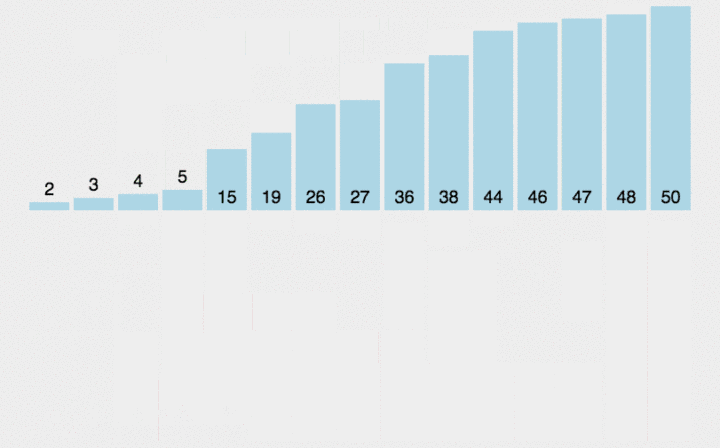
实现:
// hello.c
#include "hello.h"
void insertion_sort(int arr[], int array_length) {
for (int i = 1; i < array_length; ++i) {
int data = arr[i];
int j = 0;
while (arr[j] < arr[i])
j++;
for (int k = i; k >= j + 1; k--)
arr[k] = arr[k - 1];
arr[j] = data;
}
}
int main() {
int arr[arr_len] = {6, 5, 3, 1, 8, 7, 2, 4};
insertion_sort(arr, arr_len);
print_array(arr, arr_len);
return 0;
}
2.折半插入排序
思想:
折半插入排序是在直接插入排序的基础上改进了查找正确插入位置,即把遍历查找改成了折半查找。
实现:
// hello.c
#include "hello.h"
void binary_insertion_sort(int arr[], int array_length) {
int i, j, low = 0, high = 0, mid;
int temp = 0;
for (i = 1; i < array_length; i++) {
low = 0;
high = i - 1;
temp = arr[i];
while (low <= high) {
mid = (low + high) / 2;
if (arr[mid] > temp) {
high = mid - 1;
} else {
low = mid + 1;
}
}
for (j = i; j > low; j--) {
arr[j] = arr[j - 1];
}
arr[low] = temp;
}
}
int main() {
int arr[arr_len] = {6, 5, 3, 1, 8, 7, 2, 4};
binary_insertion_sort(arr, arr_len);
print_array(arr, arr_len);
return 0;
}
3.希尔排序
思想:
希尔排序,又称缩小增量排序。此处说的增量,即步长(step)。原始步长一般定为数组长度的一半,然后每轮遍历步长缩小为原来的一半,所以称为缩小增量排序。通过前面几轮循环,数组整体已经实现了基本有序(大多数元素序列有序),直到最终步长为1也就只需要做少量的调整,故效率高。但希尔排序的实际效率无法准确计算出来,一般认为希尔排序的时间复杂度为O(n^1.3~2)。
解释以下什么叫步长:比如一个长度为10的数组,初始步长为5,那么就把arr[0]和arr[5]看作是一组,组内进行插入排序,然后arr[1]和arr[6]又是一组,以此类推。一轮循环过后步长减半到2,arr[0]、arr[2]、arr[4]、arr[6]、arr[8]看作是一组,组内进行插入排序。
希尔排序过程推荐看旧金山大学官网的动图效果。点击Shell Sort即可
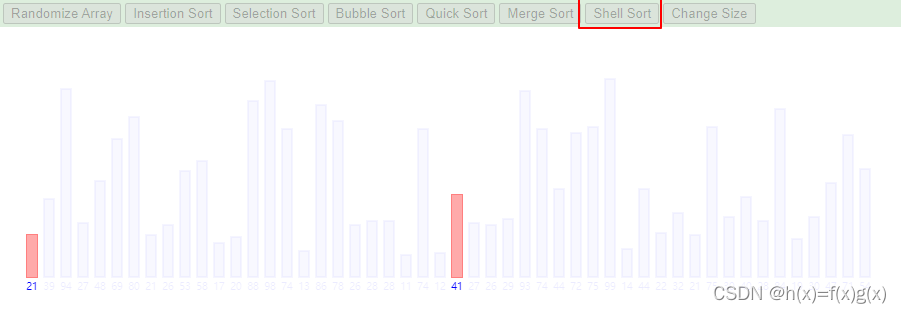
实现:
// hello.c
#include "hello.h"
void shell_sort(int arr[], int array_length) {
int step = array_length / 2;
while (step >= 1) {
for (int i = 0; i < array_length; i += step) {
int data = arr[i];
int j = 0;
while (arr[j] < arr[i])
j++;
for (int k = i; k >= j + 1; k--)
arr[k] = arr[k - 1];
arr[j] = data;
}
step = step / 2;
}
}
int main() {
int arr[arr_len] = {6, 5, 3, 1, 8, 7, 2, 4};
shell_sort(arr, arr_len);
print_array(arr, arr_len);
return 0;
}
4.冒泡排序
思想:
两两交换。通过一遍一遍的交换把大的元素交换到后面去。“大数下沉”和“小数上浮”都是这一思想的体现。
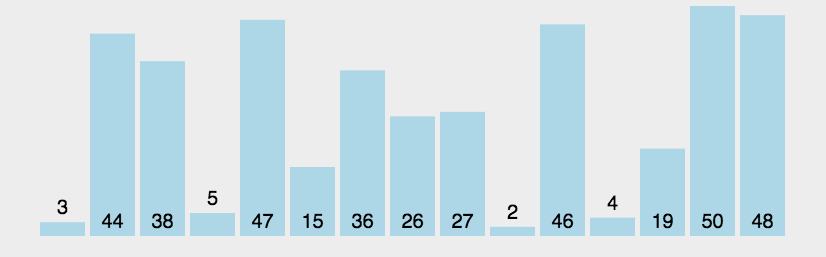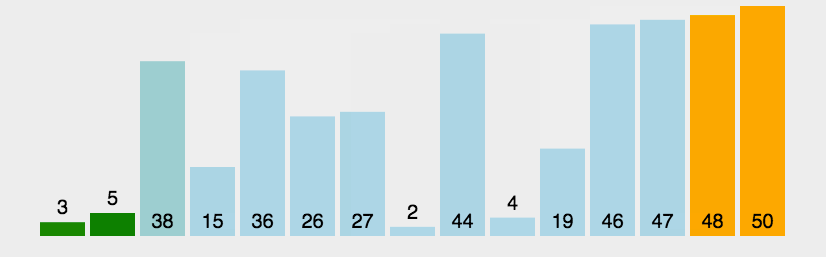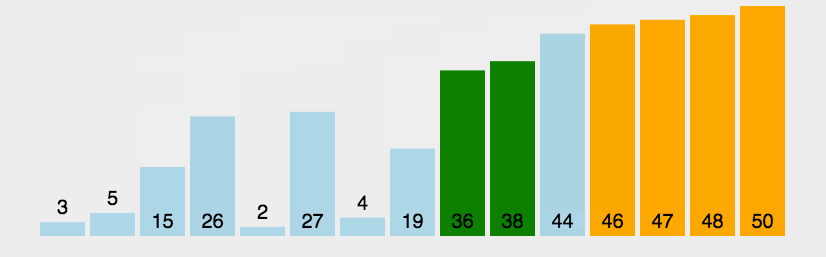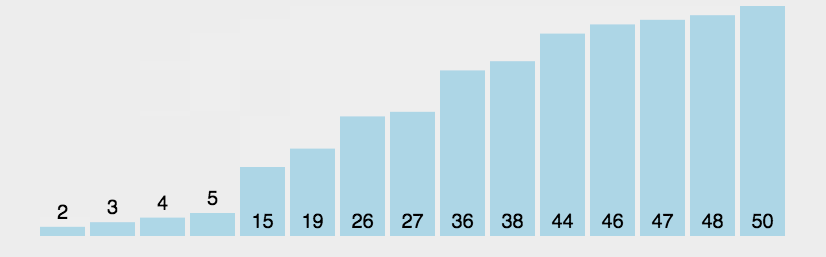
实现:
// hello.c
#include "hello.h"
void bubble_sort(int arr[], int array_length) {
for (int i = 0; i < array_length - 1; ++i) {
for (int j = 0; j < array_length - i - 1; ++j) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
int main() {
int arr[arr_len] = {6, 5, 3, 1, 8, 7, 2, 4};
bubble_sort(arr, arr_len);
print_array(arr, arr_len);
return 0;
}
5.快速排序
思想:
理解快速排序的关键在于理解flag,通过左右两个指针向中间移动,比flag小的出现在右边就交换,比flag大的出现在左边就交换,一轮过后flag出现在它最终会出现的位置。快速排序中同样也用到了分治的思想,对每个分治的部分最终实现了“左小、flag、右大”的大致排序,分治则保证了整体的有序。

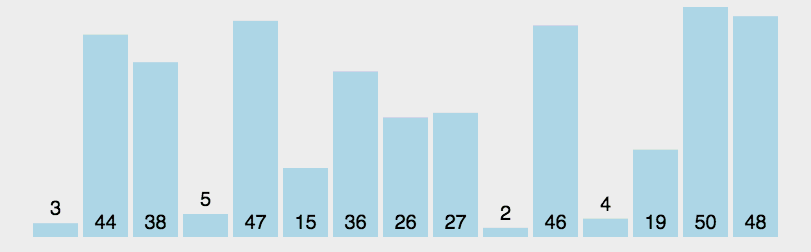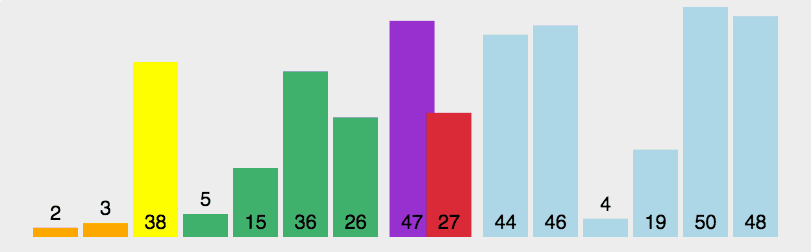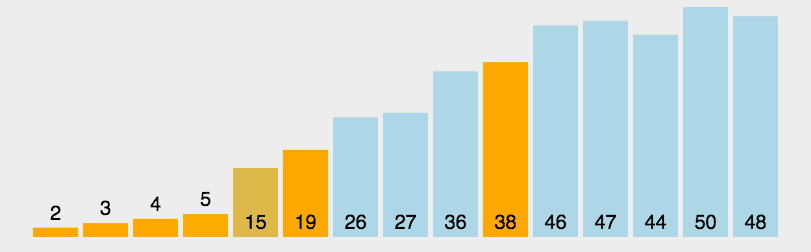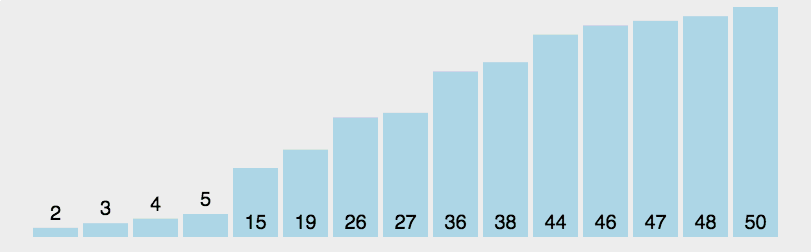
实现:
// hello.c
#include "hello.h"
int getStandard(int arr[], int low, int high) {
int flag = arr[low];
while (low < high) {
while (low < high && arr[high] >= flag) {
high--;
}
if (low < high) {
arr[low] = arr[high];
}
while (low < high && arr[low] <= flag) {
low++;
}
if (low < high) {
arr[high] = arr[low];
}
}
arr[low] = flag;
return low;
}
void quick_sort(int arr[], int low, int high) {
if (low < high) {
int pos = getStandard(arr, low, high);
quick_sort(arr, low, pos - 1);
quick_sort(arr, pos + 1, high);
}
}
int main() {
int arr[arr_len] = {6, 5, 3, 1, 8, 7, 2, 4};
quick_sort(arr, 0, arr_len - 1);
print_array(arr, arr_len);
return 0;
}
6.直接选择排序
思想:
每轮选一个最小的元素,放到它最终的位置上。
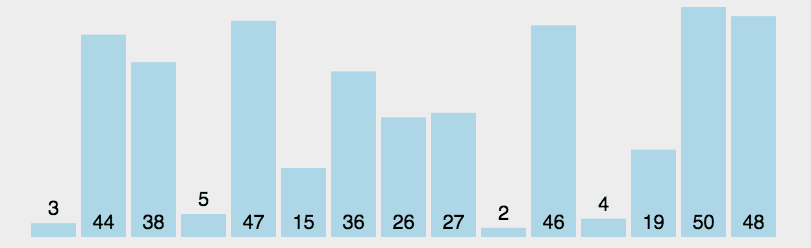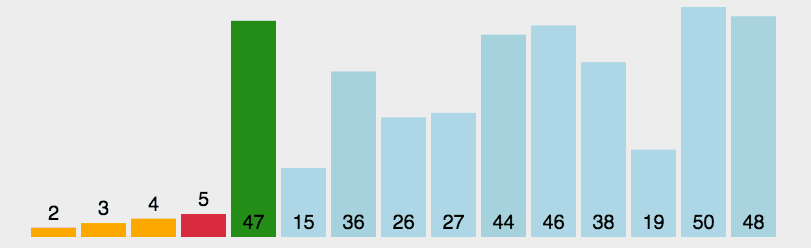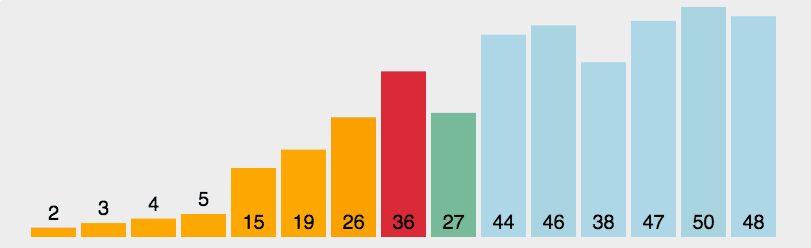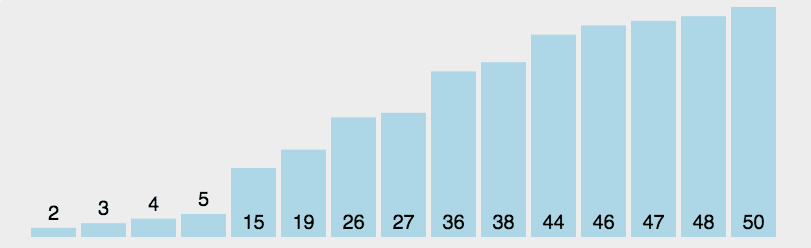
实现:
// hello.c
#include "hello.h"
void select_sort(int arr[], int array_length) {
for (int i = 0; i < array_length; ++i) {
int min_pos = i;
for (int j = i; j < array_length; ++j) {
if (arr[min_pos] > arr[j])
min_pos = j;
}
int temp = arr[min_pos];
arr[min_pos] = arr[i];
arr[i] = temp;
}
}
int main() {
int arr[arr_len] = {6, 5, 3, 1, 8, 7, 2, 4};
select_sort(arr, arr_len);
print_array(arr, arr_len);
return 0;
}
7.堆排序
思想:
堆排序充分利用了完全二叉树的特点。任意一个父节点大于它的子节点,这样的完全二叉树叫做大顶堆;与之相反的,任意一个父节点小于它的子节点,这样的完全二叉树叫做小顶堆。
堆排序过程:把元素个数为n的完全二叉树转换为大顶堆,然后把堆顶和最后一个元素交换,此时产生了一个元素个数为n-1的完全二叉树,然后再转换为大顶堆,继续把堆顶和最后一个元素交换。循环往复就实现了排序。其实质还是选择排序,每次选出一个最大的,和最后一个交换,不过完全二叉树中选最大元素比遍历数组会快很多。
堆排序的思想并不难,按照下图推演一遍就懂了。
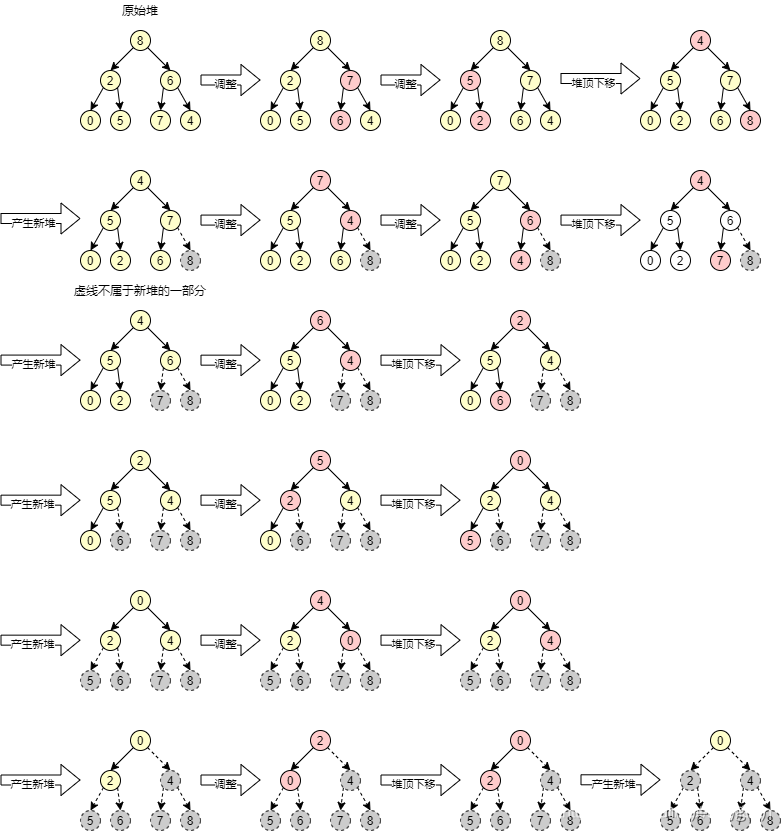
实现:
// hello.c
#include "hello.h"
void heap_adjust(int arr[], int n) {
for (int i = n / 2; i >= 1; i--) {
if (arr[i - 1] < arr[2 * i - 1]) {
int temp = arr[i - 1];
arr[i - 1] = arr[2 * i - 1];
arr[2 * i - 1] = temp;
}
if (arr[i - 1] < arr[2 * i] && (2 * i) < n) {
int temp = arr[i - 1];
arr[i - 1] = arr[2 * i];
arr[2 * i] = temp;
}
}
}
void heap_sort(int arr[], int array_length) {
int n = array_length;
do {
heap_adjust(arr, n);
int temp = arr[0];
arr[0] = arr[n - 1];
arr[n - 1] = temp;
} while (n-- && n != 0);//加了个n!=0为了跳过最后一次循环中n=0时arr[0]=arr[n-1]的数组越界错误,实际上只剩一个元素不用再调整堆了
}
int main() {
int arr[arr_len] = {6, 5, 3, 1, 8, 7, 2, 4};
heap_sort(arr, arr_len);
print_array(arr, arr_len);
return 0;
}
8.归并排序
思想:
归并的意思就是把多个集合并成一个有序的集合。两个集合进行归并操作就称为二路归并,多个集合归并就称为多路归并算法。在内排序中提到的归并排序往往是指二路归并,多路归并在外排序中有使用,这里暂且不谈。
所以归并算法的核心就是归并,如何把多个元素集合合并成一个元素集合。但我们拿到的初始集合本身就是一个完整的集合,首先还是要用分治的思想把一个集合分解成多个集合,此时多个集合间保持了原始的无序性,然后再用归并思想进行合并。所以归并排序=分支+合并,如图所示。
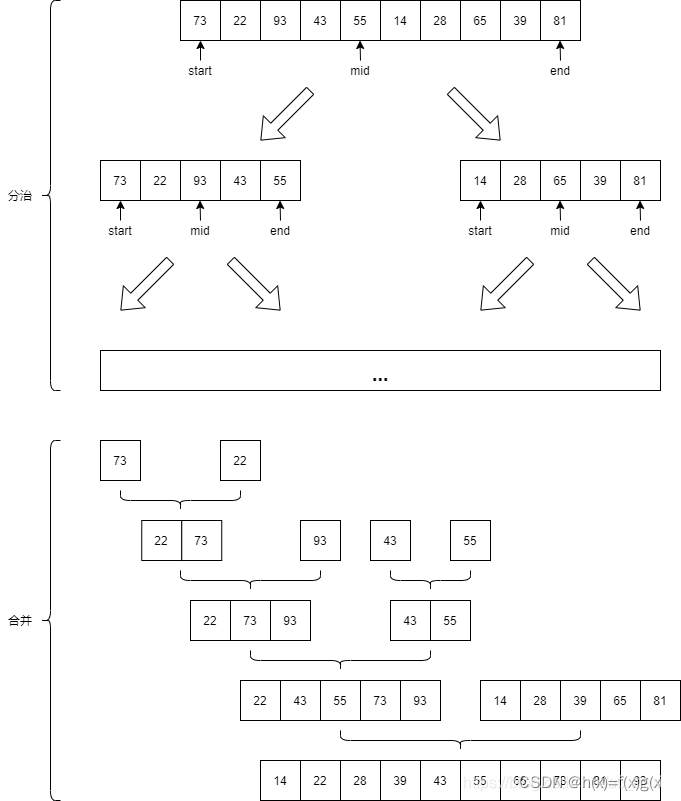
实现:
// hello.c
#include "hello.h"
void merge(int arr[], int start, int mid, int end) {
int *new_array = (int *) malloc(sizeof(int) * (end - start + 1));
int i = start;
int j = mid + 1;
int k = 0;
while (i <= mid && j <= end) {
if (arr[i] < arr[j])
new_array[k++] = arr[i++];
else
new_array[k++] = arr[j++];
}
while (i <= mid)
new_array[k++] = arr[i++];
while (j <= end)
new_array[k++] = arr[j++];
for (int l = 0; l < k; ++l)
arr[start + l] = new_array[l];
free(new_array);
}
void merge_sort(int arr[], int start, int end) {
int mid = (start + end) / 2;
if (start >= end)
return;
merge_sort(arr, start, mid);
merge_sort(arr, mid + 1, end);
merge(arr, start, mid, end);
}
int main() {
int arr[arr_len] = {6, 5, 3, 1, 8, 7, 2, 4};
merge_sort(arr, 0, arr_len - 1);
print_array(arr, arr_len);
return 0;
}
9.基数排序
思想:
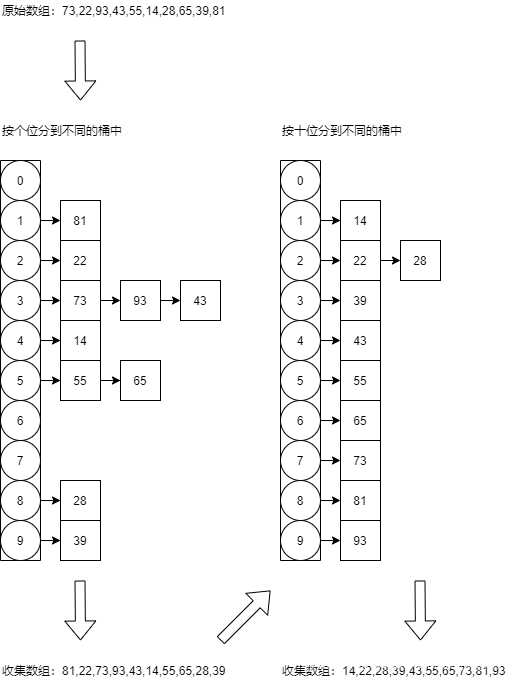
基数排序是利用元素自身的构成规律进行排序的算法。比方说一个3位数的数字,有“百位”、“十位”、“个位”,先按照“百位”对所有元素进行排序,再按照“十位”对所有元素进行排序,最后按照“个位”对所有元素进行排序,最终实现整体排序。而基数排序中用到了一个“桶”的概念,有点类似Hash桶,如下图所示。先按高进制位把元素放到不同的桶中,一轮过后再收集起来,再按低进制位重复上述步骤。理解了基数排序的原理再看动图就懂了。
基数排序还可以用于例如二进制串的比较等,这类待排序元素具有可拆分的特征的数据。

实现:
// hello.c
#include "hello.h"
int get_num(int number, int pos) {
int num = 0;
while (pos--) {
num = number % 10;
number = number / 10;
}
return num;
}
void radix_sort(int arr[], int array_length) {
int *bucket[10];
for (int i = 0; i < 10; ++i) {
bucket[i] = (int *) malloc(sizeof(int) * array_length + 1);
bucket[i][0] = 0;//桶的第一位保存桶中元素个数
}
for (int b = 1; b <= 31; ++b) {
for (int i = 0; i < array_length; ++i) {
int num = get_num(arr[i], b);//计算每个位上的数字(个位、十位、百位...)
int index = ++bucket[num][0];//计算下标
bucket[num][index] = arr[i];//保存到桶中
}
for (int i = 0, k = 0; i < 10; i++) {
for (int j = 1; j <= bucket[i][0]; ++j) {
arr[k++] = bucket[i][j];//从桶里面按顺序取出来
}
bucket[i][0] = 0;//下标清零
}
}
}
int main() {
int arr[arr_len] = {6, 5, 3, 1, 8, 7, 2, 4};
radix_sort(arr, arr_len);
print_array(arr, arr_len);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号