算法1（汉诺塔问题）

汉诺塔问题

由来：

　　大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。
　　大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。
　　在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。
　　64根柱子移动完毕之日，就是世界毁灭之时。

问题解析：

n=2时：
1.把小圆盘从A移动到B
2.把大圆盘从A移动到C
3.把小圆盘从B移动到C

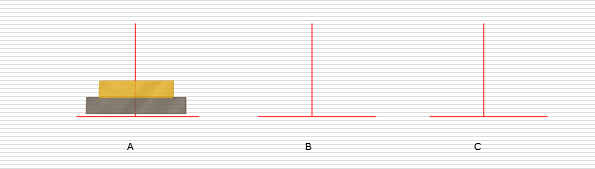
n个盘子时：
1.把n-1个圆盘从A经过C移动到B
2.把第n个圆盘从A移动到C
3.把n-1个小圆盘从B经过A移动到C

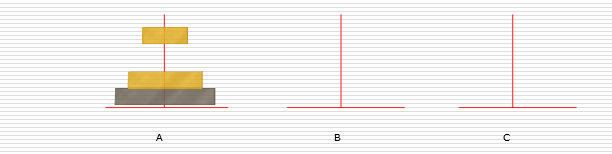
代码示例：

def hanoi(n, a, b, c):
    if n > 0:
        # n个盘子从a经b到c
        hanoi(n - 1, a, c, b)
        print('%s---->%s' % (a, c))
        hanoi(n - 1, b, a, c)

hanoi(2, 'a', 'b', 'c')

由来解析

汉诺塔移动次数的递推式：h(x)=2h(x-1)+1
h(64)=18446744073709551615
假设婆罗门每秒钟搬一个盘子，则总共需要5800亿年