[转载]Power Series and Functions

转载自    https://tutorial.math.lamar.edu/Classes/CalcII/PowerSeriesandFunctions.aspx

 

在这一章节我们开始讨论如何用幂级数来表示一个函数，或者说如何将一个函数写成幂级数的形式。为什么想要把一个函数写成幂级数的形式呢？在后面的章节中会解答这个问题。

让我们从一个已知的事例也就是几何级数（或者称之为等比数列）来开始，尽管在我们初次见到这个函数的时候不觉得他是幂级数。让我们回顾一下他 ：

式子中provided是假设的意思

$ \sum\limits_{n = 0}^\infty {a{r^n}} = \frac{a}{{1 - r}}\hspace{0.5in}{\mbox{provided }}\left| r \right| < 1 $

 不要忘记当r的绝对值大于1时，这个级数没有一个确定的值，或者直译为不收敛。

如果把a换成1，r换成x，那么公式为

$ \sum\limits_{n = 0}^\infty {{x^n}} = \frac{1}{{1 - x}}\hspace{0.5in}{\mbox{provided }}\left| x \right| < 1 $

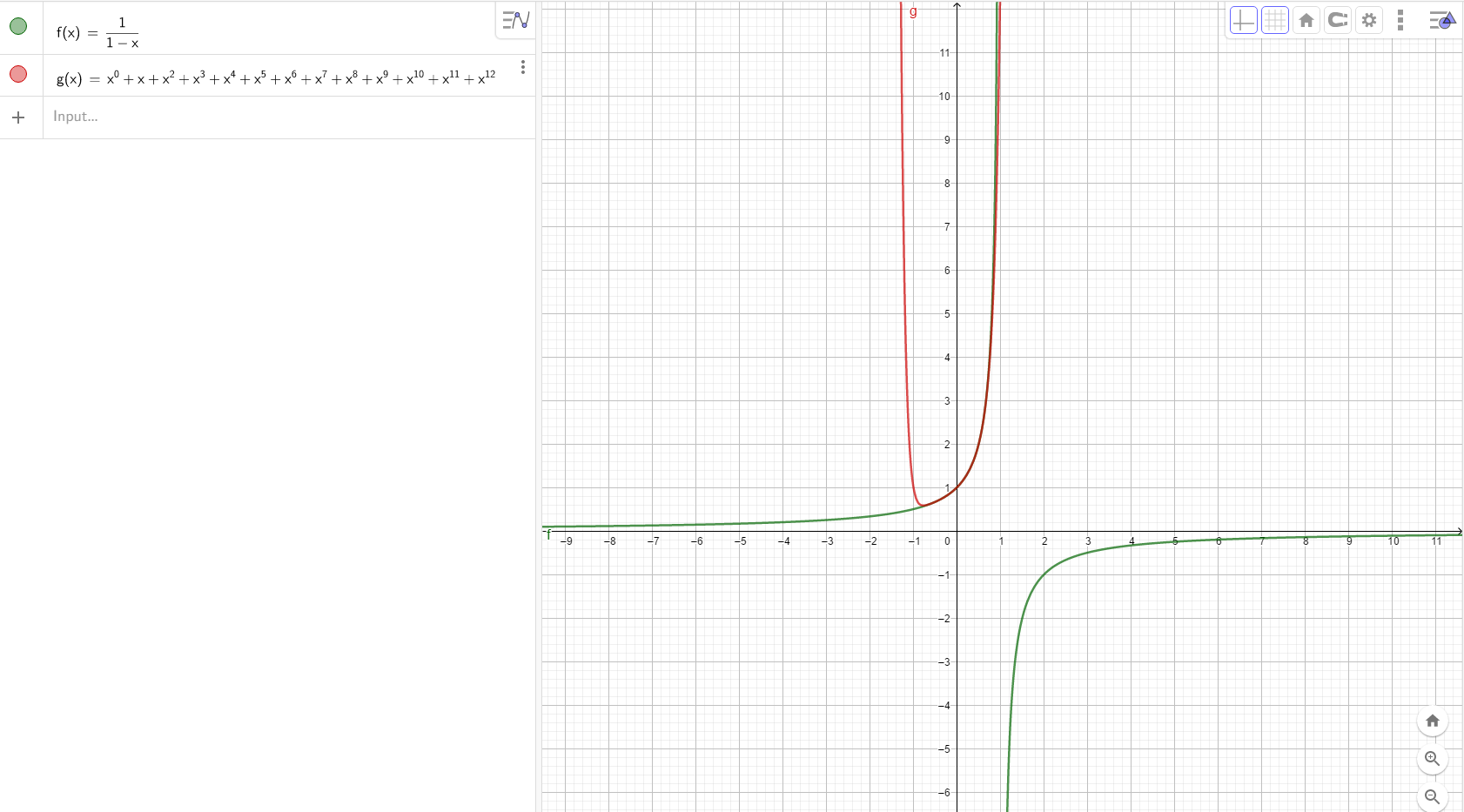
回过头来看，我们把函数 $ f\left( x \right) = \frac{1}{{1 - x}}  $用幂级数$ \sum\limits_{n = 0}^\infty {{x^n}} \hspace{0.5in}{\mbox{provided }}\left| x \right| < 1 $来表示

这个准备过程很重要，我们可以把任何一个不是1的数代替x填充进去，但是只有当$ \left| x \right| < 1 $（x的绝对值小于1时）这个幂级数才是收敛的（无穷个数字加起来的值是趋近于一个固定的值的）。当x取其他值的时候幂级数不收敛。

收敛的概念是很重要的，因为我们会用幂级数去表示很多的函数，要意识到只有x在一定的范围内这个幂级数才是收敛的，换句话说此时这个函数的幂级数的表达形式才能跟原函数对的上，才是有意义的。有的x可以代入原函数求值，但是无法代入幂级数求值，代入以后幂级数不收敛。

在这一小节，我们主要关注如何将与   $  f\left( x \right) = \frac{1}{{1 - x}}  $  有关的函数写成幂级数的形式，希望通过这种方式掌握一些常见的操作手法，这些手法在以后处理幂级数的时候会用到。

下面让我们来看一些例子

Example 1 将下面的函数写成幂级数的形式，并找到他的收敛区间

$ g\left( x \right) = \frac{1}{{1 + {x^3}}} $

解答：我们这里要做的就是想办法将这个函数与 $ f \left( x \right) = \frac{1} {{1 - x}}  $ 扯上关系。

怎么做呢？很简单

$ g\left( x \right) = \frac{1}{{1 - \left( { - {x^3}} \right)}} $

所以g(x)中的$ - {x^3} $所处的地位就等同于 $  f\left( x \right) = \frac{1}{{1 - x}}  $  中的x所处的地位。所以代入到级数的表达式中，得到g(x)的幂级数形式为：

 $  g\left( x \right) = \sum\limits_{n = 0}^\infty {{{\left( { - {x^3}} \right)}^n}} \hspace{0.5in}{\mbox{provided }}\left| { - {x^3}} \right| < 1   $

无论是在表达式中代入还是在求x的范围的时候，注意到我们把 $   - {x^3}   $ 当做一个整体。

现在我们把上面的表达式简化一下

$   g\left( x \right) = \sum\limits_{n = 0}^\infty {{{\left( { - 1} \right)}^n}{x^{3n}}} \hspace{0.5in}{\mbox{provided }}{\left| x \right|^3} < 1\hspace{0.25in} \Rightarrow \hspace{0.25in}\left| x \right| < 1   $

发现在这种情况下，幂级数保持收敛的x的区间与原始的幂级数保持收敛的区间一致

 

 

 

 Example 2 将下面的函数写成幂级数的形式，并找到他的收敛区间

 $  h\left( x \right) = \frac{{2{x^2}}}{{1 + {x^3}}}  $

这个函数与之前的函数很像。区别在于分子不同，猛然看起来似乎跟之前的函数差别很大，因为之前的函数分子上没有x并且似乎我们无法将现在的函数与之前的那个扯上关系

然而，我们做过了第一个例子，那么我们可以用第一个例子的结论。怎么操作呢？我们先以另一种形式来写这个函数

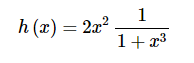
根据第一个例子，我们已经得到了第二个部分，也就是 $ \frac{1}{{1 + {x^3}}}   $ 这个部分，的幂级数形式，让我们用这个形式重新写一下这个函数 

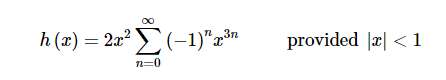
注意到在求和符号外边的x不会影响到他的收敛性，或者说唯一确定性，所以收敛区间不变

最后一步是将求和符号外边的系数移进求和符号内，就是对这个式子做一个化简。毕竟同类项放在一块比较顺眼。

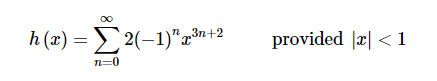
正如我们在前面的例子中看到的，我们可以使用之前得到的结论来解决现在遇到的问题。这种思想一定要重视，因为他会大大简化我们的工作。

 

Example 3 将下面的函数写成幂级数的形式，并找到他的收敛区间

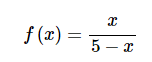
又一次，分子上出现了x。就像上面的例子，我们把x提出来，然后看看得到了什么

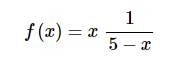
如果我们可以将

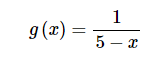
写成幂级数形式，那么我们就可以把f(x)  写成幂级数形式.

怎么将它写成幂级数形式呢？

如果我们想利用 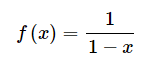的幂级数形式，那么我们首先需要把分母上的数字变为1，这个很容易做到

 

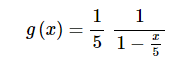
然后我们把 $  f\left( x \right) = \frac{1}{{1 - x}}  $ 的幂级数形式中的x替换成x/5，得到

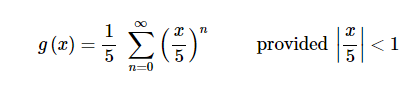
现在我们做一些简单的化简操作

 \begin{align*} g\left( x \right) & = \frac{1}{5}\,\,\sum\limits_{n = 0}^\infty {\frac{{{x^n}}}{{{5^n}}}} \\ & = \sum\limits_{n = 0}^\infty {\frac{{{x^n}}}{{{5^{n + 1}}}}} \end{align*} 

 

收敛区间为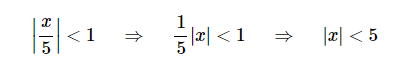

 

 现在我们得到了g(x)的幂级数形式。然后回到最初的问题，我们需要找到f(x)的幂级数形式。

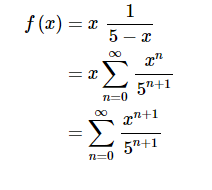
收敛区间没有变化，即为$ \left| x \right| < 5 $

现在，我们应该对找到某些函数的幂级数形式有了一些体会。思路就是所有的函数都想方设法与     $  f\left( x \right) = \frac{1}{{1 - x}}  $  扯上关系。

现在我们需要看一下那些我们可能偶然会碰到的对幂级数的操作方法。我们需要讨论一下对幂级数的积分和微分

首先我们看一下幂级数的微分

 

现在我们知道对于有限个项（比如n=10）相加的的式子，对它的微分等于分别对这有限项做微分然后相加。对于无限项相加的式子做微分，有一些特殊的技巧，但目前不在我们的讨论范围内。

如果f(x)的幂级数形式的收敛区间存在，那么对每一项的微分也有同样的收敛区间，这个收敛区间也是对f(x)作微分后得到的导数函数的收敛区间。