[读书笔记]阶跃函数的数学描述 对于式子1.67的理解 信号与系统 Signals and System by Alan V. Oppenheim, Alan S. Willsky

截图来自于Signals and System by Alan V. Oppenheim, Alan S. Willsky 第2版

 

 

 

 

 

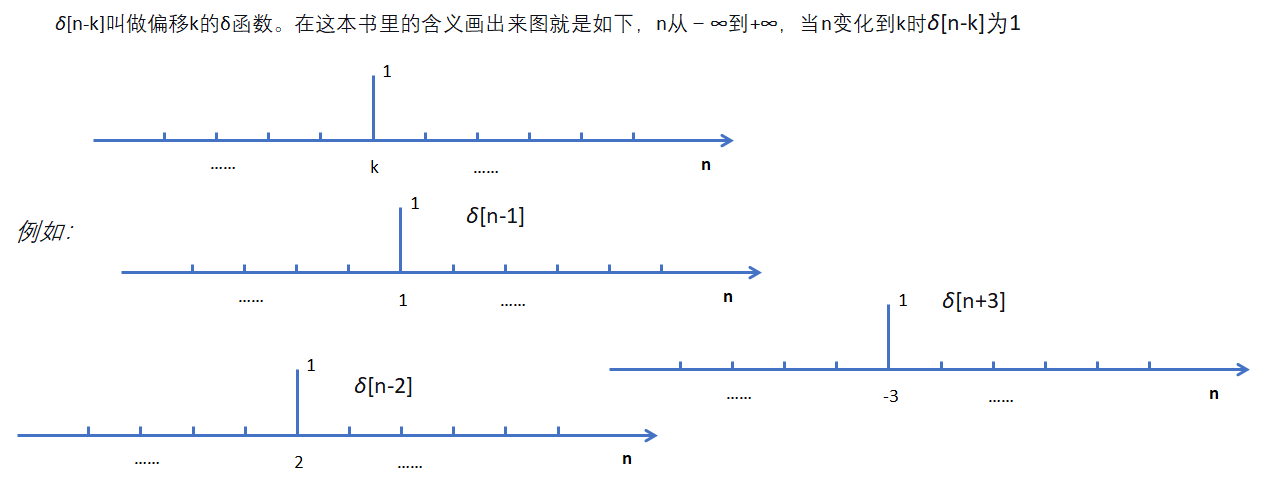
k为正数时，相当于将脉冲序列向右移动k个单位，当k为负数时，相当于将脉冲序列左移k个单位.。而n是这个信号的自变量，n可以取的范围就是信号存在的范围，在这里不是关注的重点，重点是k表示信号的平移。

对于式子1.67该怎么理解。先不管n为多少，先看k所有可能的范围以及对应于每个k的delta函数。这些每个k对应的delta函数相加才是n为自变量时对应的函数的样子

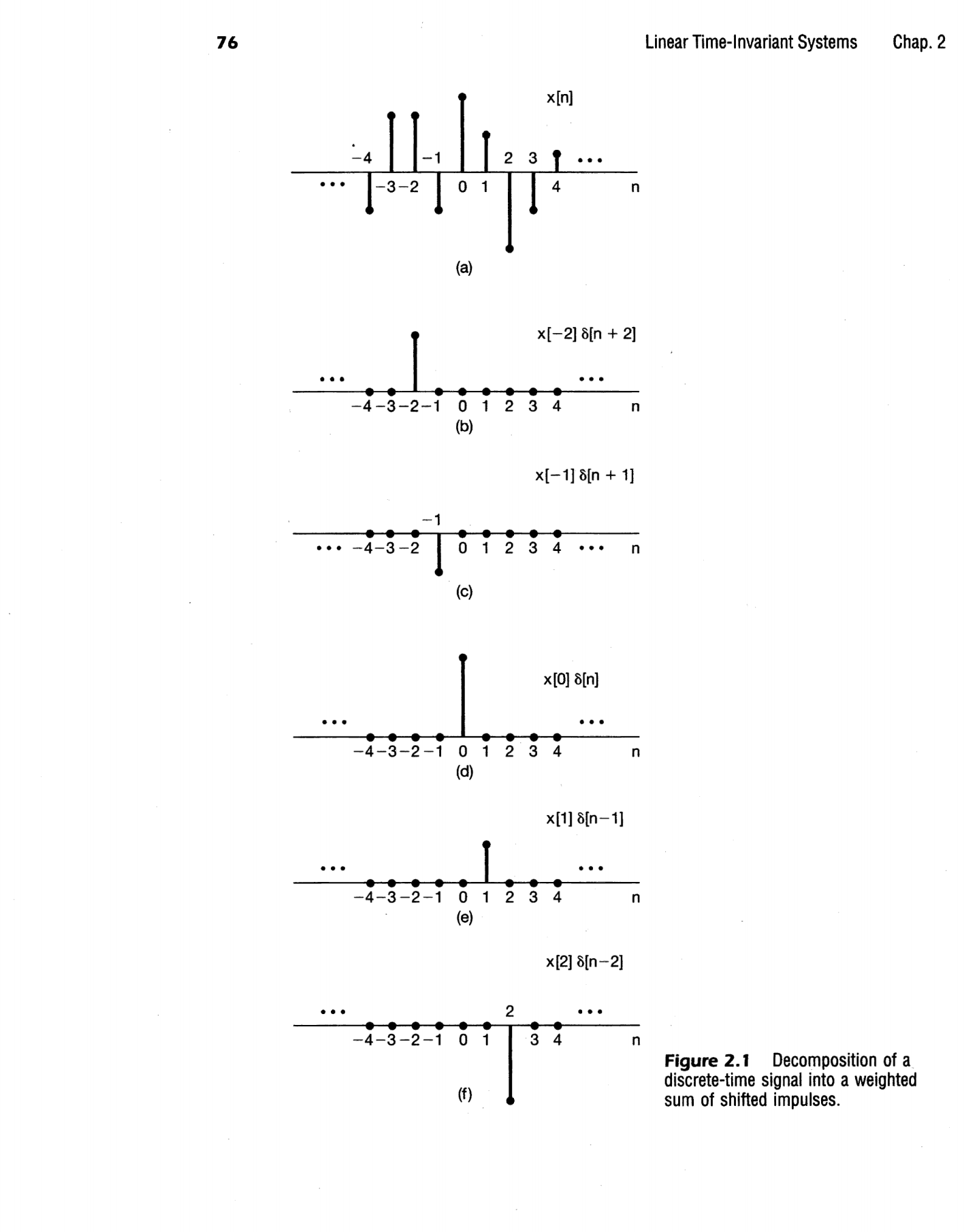
由这个式子引申，如下页中的式2.2，对于式子2.2的理解如示意图所示。即为右侧每一个k都对应一组值，这一组值是以n为自变量的值，是k处的信号对应的信号反馈。每一个k对应的这一组值相加，就得到对于整体的信号输入的整体信号反馈。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

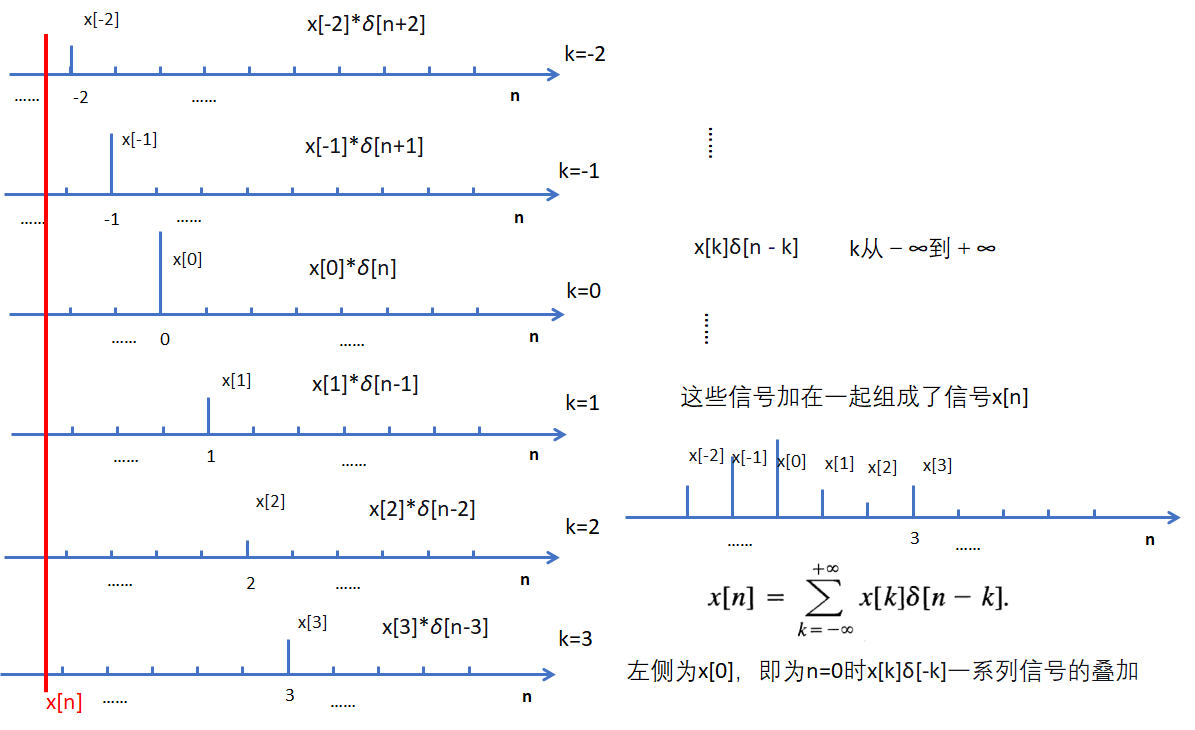
再引申一步，如果对于k处的信号输入，用$  h_k\left ( n \right ) $表示对于k处的信号输入的反馈，那么

 

 

 

 

 

k处的信号乘以平移到k处的对单位信号反馈，然后将这些累加起来，就是卷积