[读书笔记]平面波的数学表示 Optics 5th 作者Eugene Hecht
截图来自于Optics 5th 作者Eugene Hecht
比较懒,就直接截图了,哈哈哈哈哈~


对于公式2.46 $ \psi \left ( \vec{r} \right )=Ae^{i\vec{k}\cdot \vec{r}} $而言,自变量是什么,是在空间的位置$ \vec{k}\cdot \vec{r} $, $ \vec{k} $是指向波传播方向的向量,$ \vec{r} $是任意一个向量,或者说在确定的坐标系中,任何一个点的位置都可以理解成一个从原点出发指向这个点所在位置的向量,$ \vec{r} $是任意一个向量,也可以理解为$ \vec{r} $是空间中任意一个位置,当$ \vec{k}\cdot \vec{r} $是一个常数时,$ \vec{r} $的端点组成的是一个平面,为啥呢?这就涉及到向量点乘的定义,在此不再赘述。在这个平面上$ \vec{k}\cdot \vec{r} $是一个常数,在公式中这个常数表示的是相位,也就是说在这个平面内$ e^{i\vec{k}\cdot \vec{r}} $相位相同。如果$ \vec{k} $指向的是x轴,如图2.22所示,那么$ \psi \left ( \vec{r} \right )=Ae^{i\vec{k}\cdot \vec{r}} $可以简化为$ \psi \left ( \vec{r} \right )=Ae^{ikx} $,此时垂直于x轴的平面上的任何一个点与平面内其他点的相位相同。


Mathematica 代码演示
在https://www.wolframcloud.com/中输入如下代码
Graphics3D[Hyperplane[{0,1,0},{0,1,0}],PlotRange->{{-5,5},{-5,5},{-5,5}},Axes->True,AxesLabel->{x,y,z}]
Hyperplane[{0,1,0},{0,1,0}]的意思就是生成一个垂直于前面一个向量{0,1,0}的平面,这个平面过后面一个点{0,1,0}
用Graphics3D[]画成3D的图像,并指定画的范围为PlotRange->{{-5,5},{-5,5},{-5,5}},分别一一对应x,y,z的范围。并用AxesLabel->{x,y,z}显示坐标轴的表现,显示哪个是x轴,哪个是y轴,哪个是z轴

Manipulate[Graphics3D[Hyperplane[{0,1,0},{0,y,0}],PlotRange->{{-10,10},{-10,10},{-10,10}},Axes->True,AxesLabel->{x,y,z}],{y,1,10,1}]
用Manipulate[]来画出一个可交互的图形,改变的是平面所过的点{0,y,0},y的变化范围为{y,1,10,1} ,从1到10,每次变化1
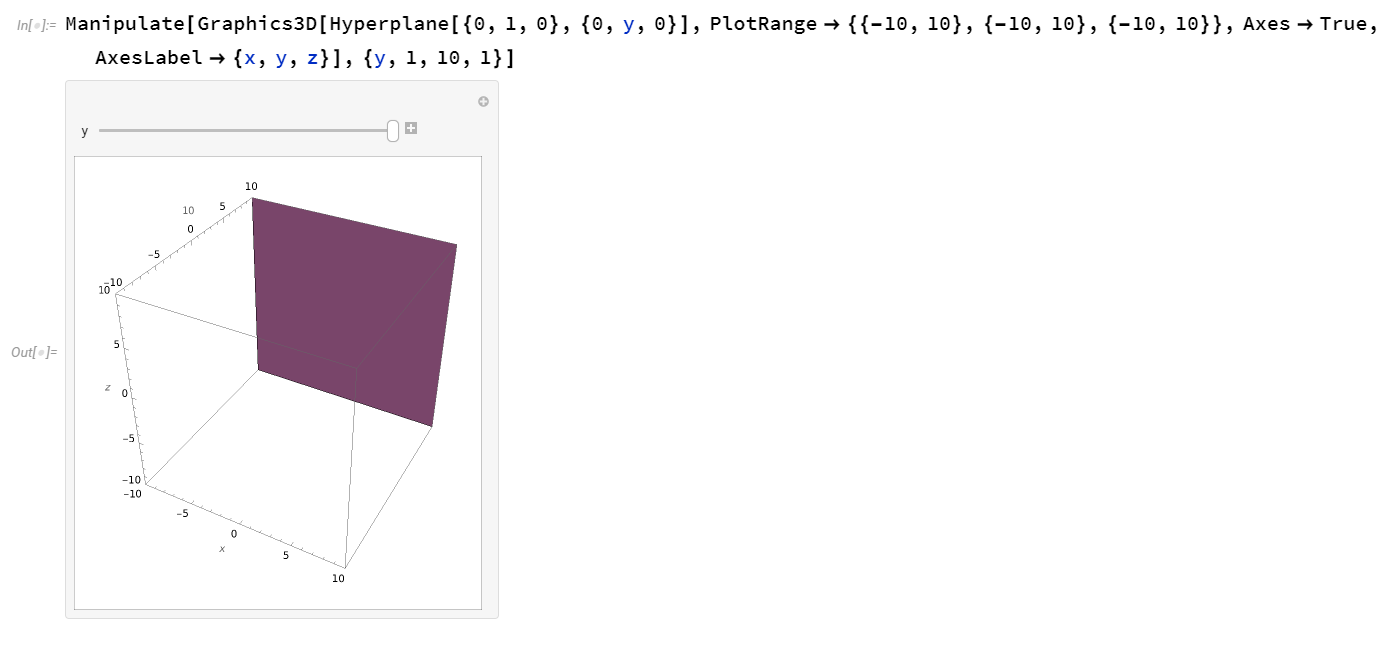
可以加深对于平面波的理解




 浙公网安备 33010602011771号
浙公网安备 33010602011771号