浅析如何在逆向中分析AES算法

AES算法浅析

AES是对称加密算法，在逆向中常常使用到，白盒AES算法详解这篇文章写的非常好，通俗易懂。但是我在原理到代码的过程经常会卡壳，因此结合C语言代码浅析一下算法。

这里使用的源码为https://github.com/kokke/tiny-AES-c

密钥扩展

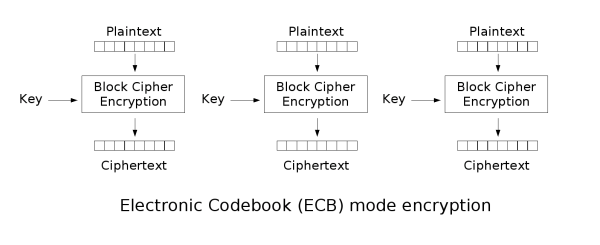
这里以AES-128为例子（以下用AES代替），初始时输入的密钥长度是16字节的，因此每次加密的长度的明文也需要与之匹配，在加密之前，需要将明文分割成16字节长度为一组，然后分割为若干组进行加密，与下图一致（ECB加密模式）。

undefined

由于AES加密需要经过10轮加密，因此需要11个密钥（每轮一个+初始一个），因此需要利用输入的初始密钥生成剩下的10个密钥，这个生成密钥的过程就称之为密钥扩展，如下图所示，k0-k3为初始密钥，每一块为4个字节。其余k4-k44就是通过初始密钥k0-k3经过密钥扩展计算得到

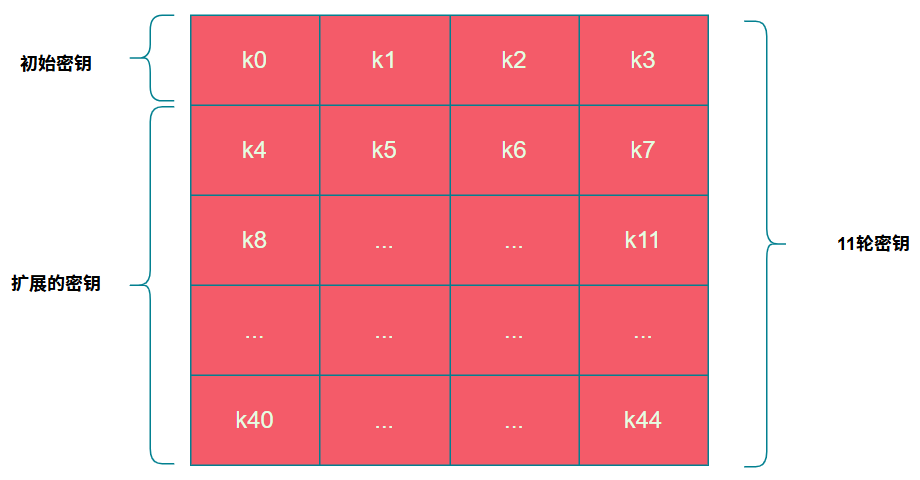
image-20251114220140556

扩展密钥依赖公式$k_n=k{n-1}\oplus k{n-4}$ 即密钥$k_5=k_4\oplus k_1$，依次类推。

但是k4、k8...k40扩展密钥比较特殊，需要经过G运算后再进行异或，即$k4=G(k_3)\oplus k_0$

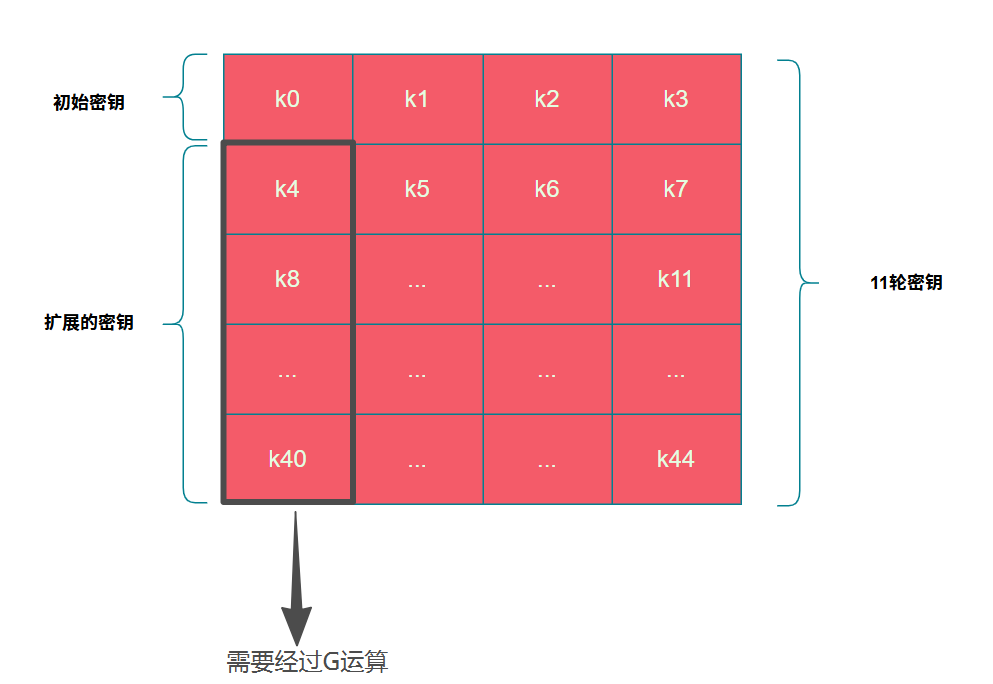
image-20251114221805876

G运算

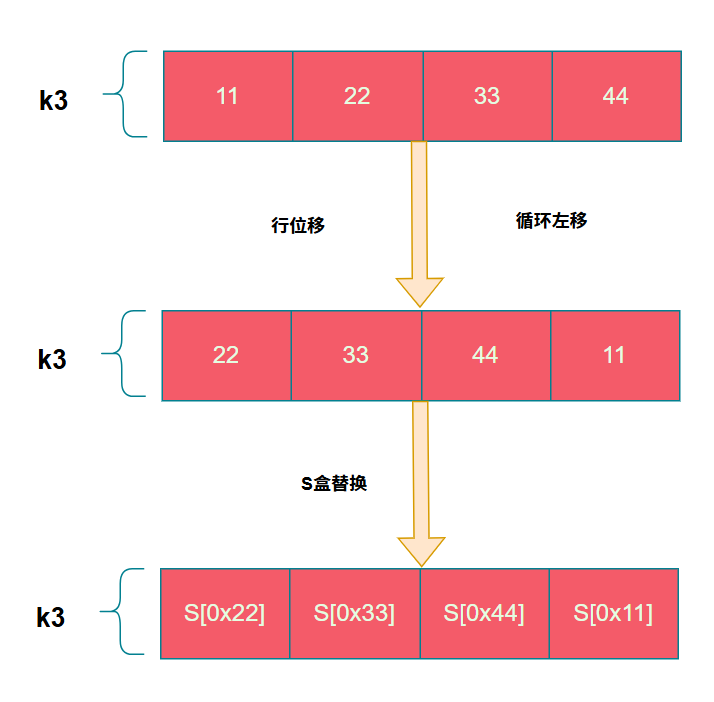
G运算就是将密钥进行行位移、S盒替换、以及跟一个常数进行异或得到最后的结果，这里我们假设k3=0x11223344

image-20251114222301745

行位移

行位移实际是做了一个循环左移的操作，将每个字节往左移动了一个字节

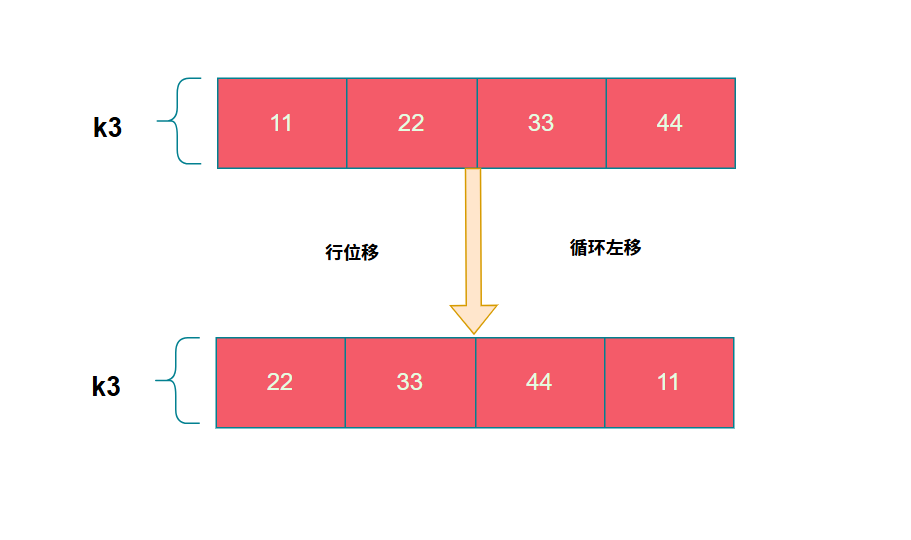
image-20251114222508769

在tiny-AES-c中行位移的实现使用字符转换实现。

...
    {
        //行位移
        const uint8_t u8tmp = tempa[0];
        tempa[0] = tempa[1];
        tempa[1] = tempa[2];
        tempa[2] = tempa[3];
        tempa[3] = u8tmp;
     }
...

S盒替换

S盒则是一个长度为256的数组，其中会放置一些具体的数值。S盒的替换则是将字节的值作为下标去数值找到对应的值。

image-20251114222911172

其中S盒的数值如下，因此可以依据S盒的值作为AES算法的特征值

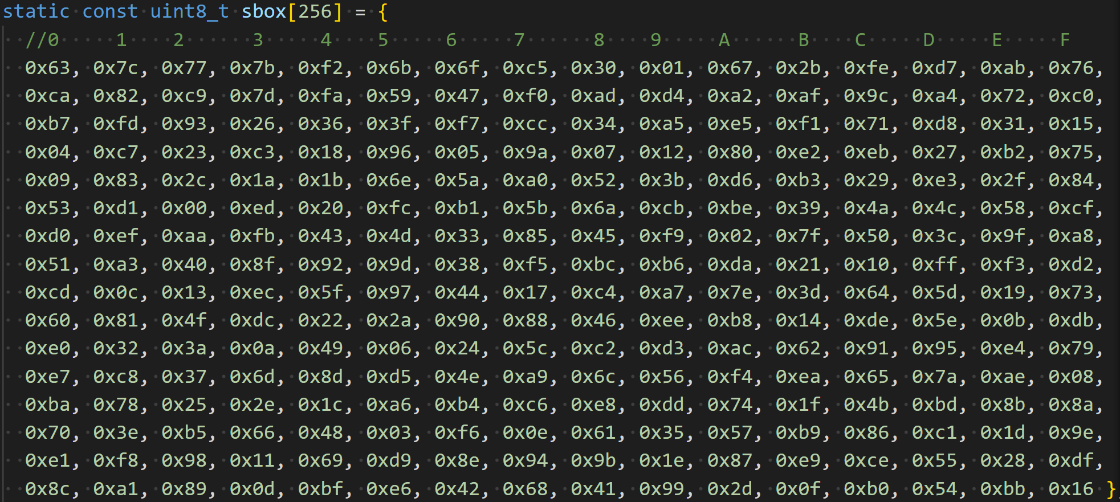
image-20251114222950328

而S盒的替换则是首先定义sbox数组，如上图。然后将行位移后的密钥字节值作为下标直接在sbox中取值，如下述代码。

#define getSBoxValue(num) (sbox[(num)])
     ...
     {
        tempa[0] = getSBoxValue(tempa[0]);
        tempa[1] = getSBoxValue(tempa[1]);
        tempa[2] = getSBoxValue(tempa[2]);
        tempa[3] = getSBoxValue(tempa[3]);
      }
     ...

常量异或

其中常量是存储在名为Rcon的数组中

image-20251114223521935

紧接着将S盒替换后的结果与这些常量进行异或，其中n代表的是轮数，刚好对应Rcon数组的10个值，用于后续10轮扩展，这里需要注意的是Rcon数组是以下标1为起始位置，并且Rcon数组每一个元素的大小只占用一个字节，因此需要使用密钥的第一个字节异或即可。

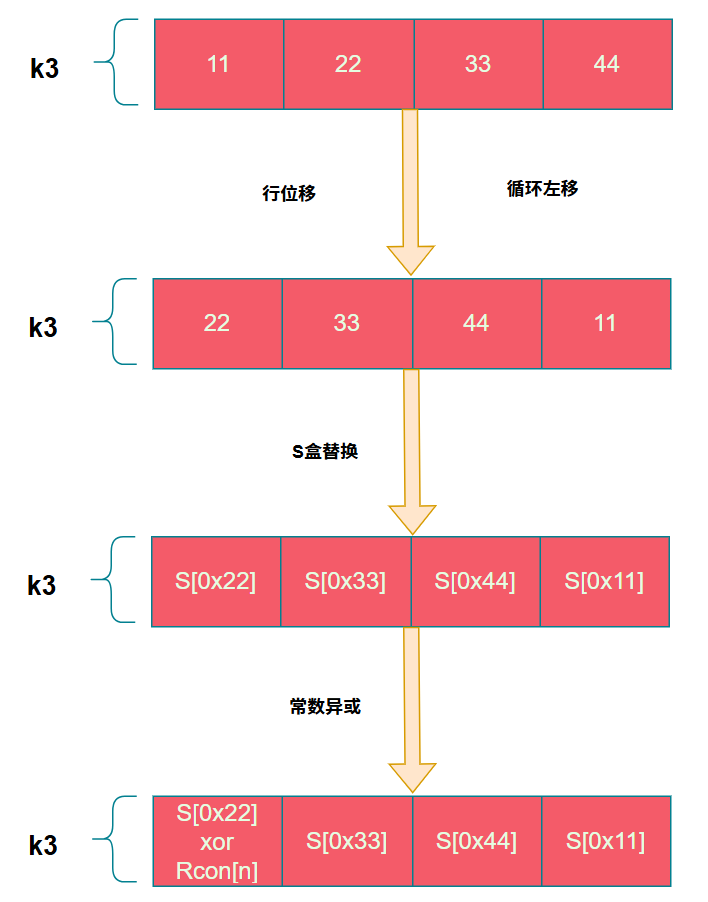
image-20251115080441547

最后一步就是常量异或，这里跟上述说的一样只需要取第一个字节异或即可，这里NK=4，那么i的值只会取$4、8、12....40$，因此$\frac{i}{NK}$刚好代表的是轮数，第一轮则使用Rcon[1]异或，第二轮则用Rcon[2]以此类推。

      //常量异或
      tempa[0] = tempa[0] ^ Rcon[i/Nk];

最终得到的值就是经过G运算后的值了，那么我们的扩展后的密钥k4则是经过G运算后的k3与k0进行异或，即$k4=G(k_3)\oplus k_0$，这里需要注意的是，代码是以字节为单位处理的，而在AES算法中$k_n$是以4字节为单位处理，所以这里处理下标的时候使用了$i*4$。无论密钥是否经过G运算，都可以使用下述代码进行异或处理，若是经过G函数那么tempa则存储$G(k{n-1})$，反之则存储$k{n-1}$

    ...
    //j为密钥具体字节的下标，k代表的是n-4,tempa数组存储经过G函数处理后的密钥字节
    j = i * 4; k=(i - Nk) * 4;
    RoundKey[j + 0] = RoundKey[k + 0] ^ tempa[0];
    RoundKey[j + 1] = RoundKey[k + 1] ^ tempa[1];
    RoundKey[j + 2] = RoundKey[k + 2] ^ tempa[2];
    RoundKey[j + 3] = RoundKey[k + 3] ^ tempa[3];
    ...

加密阶段

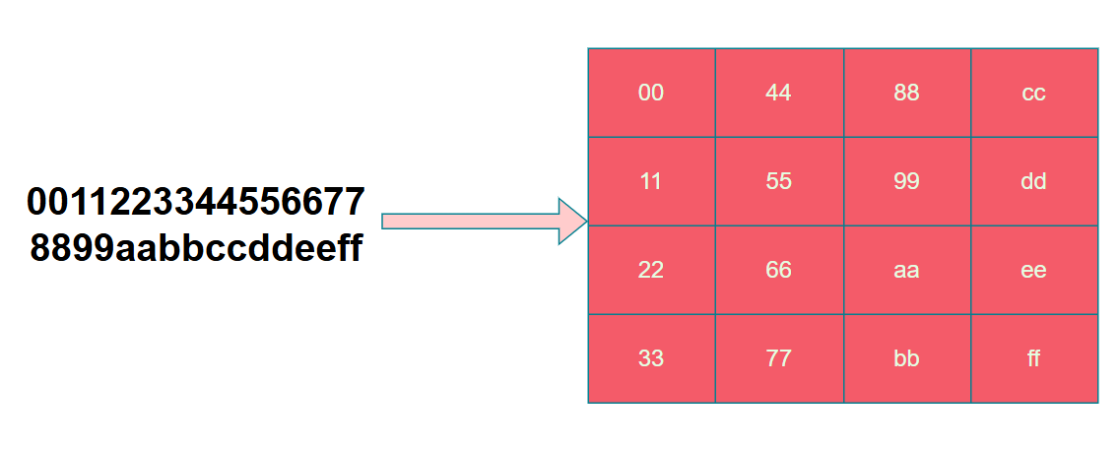
在加密之前，需要将明文转换为state，具体转换过程如下图，其实很简单，就是列存储明文数据。

image-20251115082240455

具体加密过程如下图，需要先经过轮密钥加、字节替换、行位移、列混淆，其中最后一轮不需要列混淆的操作。。

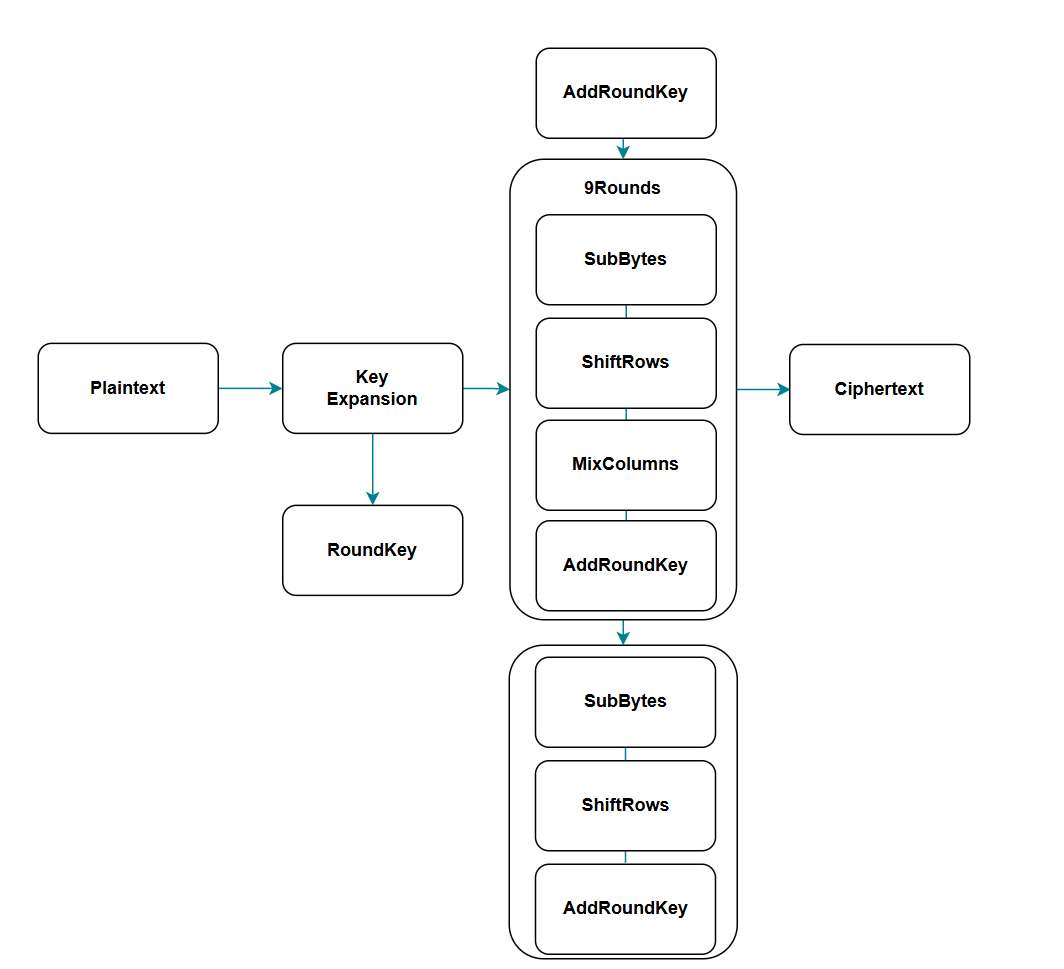
image-20251115111738651

轮密钥加

在AES算法中，加法都是异或操作，因此轮密钥加就是按字节将明文与密钥进行异或操作，如下图所示。

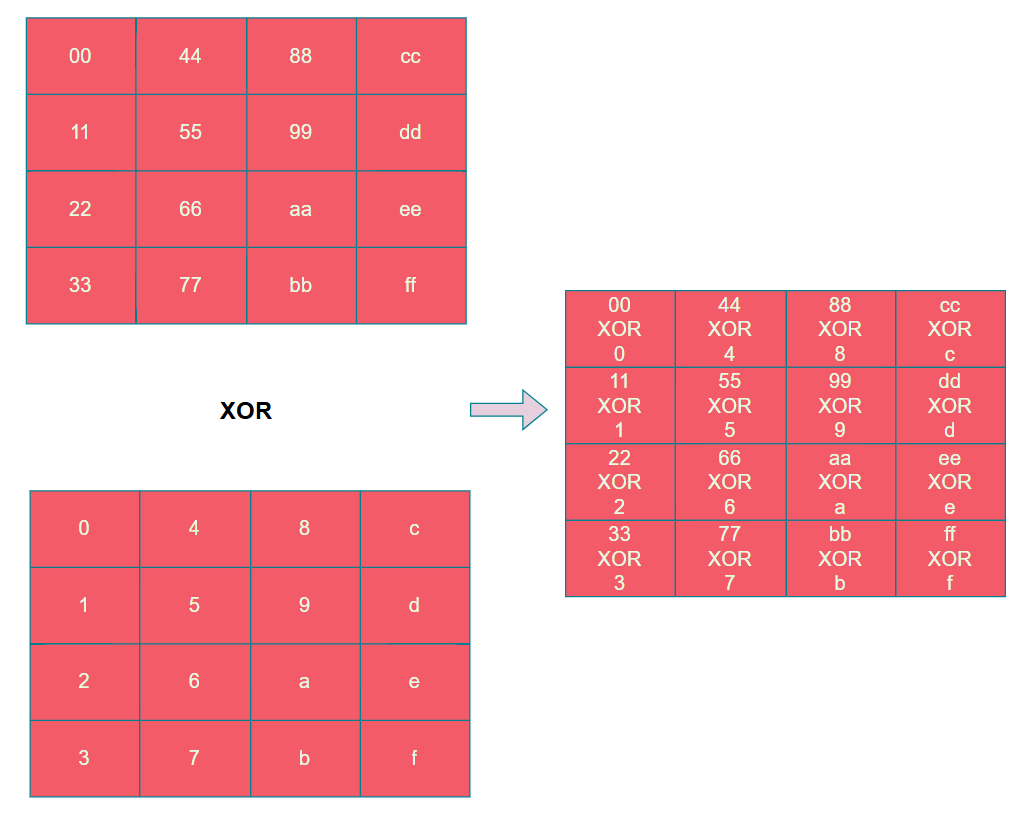
image-20251115121555484

在tiny-AES-c，state实际上是按照行进行存储的，但是轮密钥加的环节进行的字节异或，因此按照行存储的方式逐字节取出明文与密钥进行异或不会影响结果，如下列代码所示。

static void AddRoundKey(uint8_t round, state_t* state, const uint8_t* RoundKey)
{
  uint8_t i,j;
  //轮密钥加，逐个字节异或
  for (i = 0; i < 4; ++i)
  {
    for (j = 0; j < 4; ++j)
    {
      //每轮密钥是16字节
      (*state)[i][j] ^= RoundKey[(round * Nb * 4) + (i * Nb) + j];
    }
  }
}

字节替换

字节替换与密钥扩展中的S盒替换一致。这里就是行列取出字节，然后进行S盒的替换。

static void SubBytes(state_t* state)
{
  uint8_t i, j;
  for (i = 0; i < 4; ++i)
  {
    for (j = 0; j < 4; ++j)
    {
      (*state)[j][i] = getSBoxValue((*state)[j][i]);
    }
  }
}

行位移

行位移则是以state为单位，进行逐行的循环左移，如下图所示，第一行不移动，第二行移动1个字节，第三行移动2个字节，第四行移动3个字节。

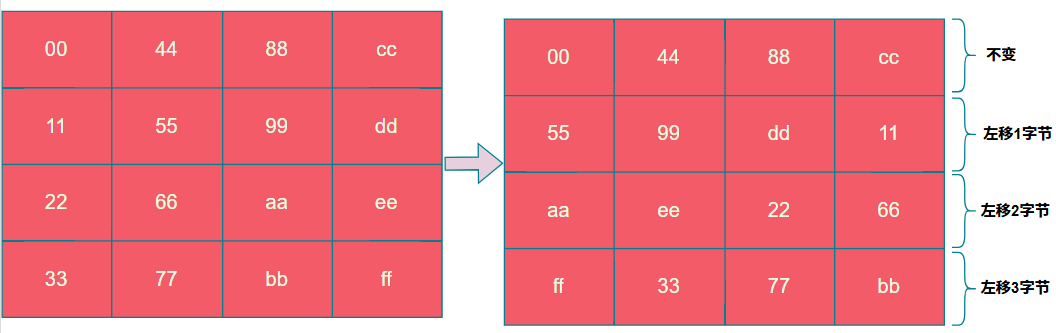
image-20251115122746408

由于在tiny-AES-c中是将明文以行存储的方式转换state的，因此移位的时候需要以列的方式进行移位。

static void ShiftRows(state_t* state)
{
  uint8_t temp;
​
  // Rotate first row 1 columns to left  
  //[1][1]移动到[0][1]向上移动1个字节
  temp           = (*state)[0][1];
  (*state)[0][1] = (*state)[1][1];
  (*state)[1][1] = (*state)[2][1];
  (*state)[2][1] = (*state)[3][1];
  (*state)[3][1] = temp;
​
  // Rotate second row 2 columns to left 
  //[2][2]移动到[2][2]向上移动2个字节  
  temp           = (*state)[0][2];
  (*state)[0][2] = (*state)[2][2];
  (*state)[2][2] = temp;
​
  temp           = (*state)[1][2];
  (*state)[1][2] = (*state)[3][2];
  (*state)[3][2] = temp;
​
  // Rotate third row 3 columns to left
  //[3][3]移动到[0][3]向上移动3个字节
  temp           = (*state)[0][3];
  (*state)[0][3] = (*state)[3][3];
  (*state)[3][3] = (*state)[2][3];
  (*state)[2][3] = (*state)[1][3];
  (*state)[1][3] = temp;
}

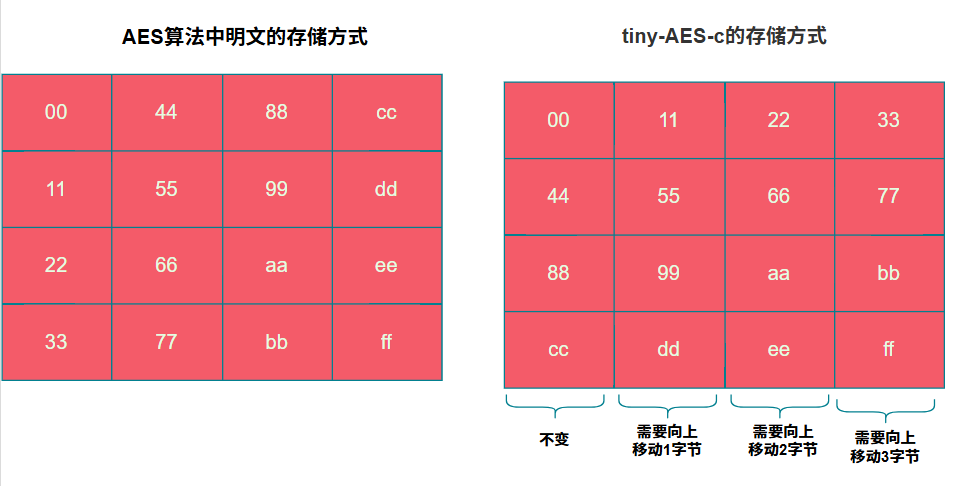
上述代码的意思如下图所示，我们只需要把表格翻转一下，那么向左移动就相当于向上移动了。

image-20251115123733254

列混淆

列混淆则是通过矩阵的乘法实现的

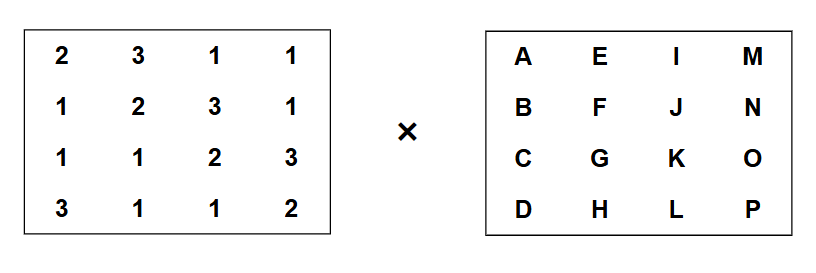
image-20251115212132121

最终得到的式子如下所示

  1. $2A+3B+C+D$

  2. $A+2B+3C+D$

  3. $A+B+2C+3D$

  4. $3A+B+C+2D$

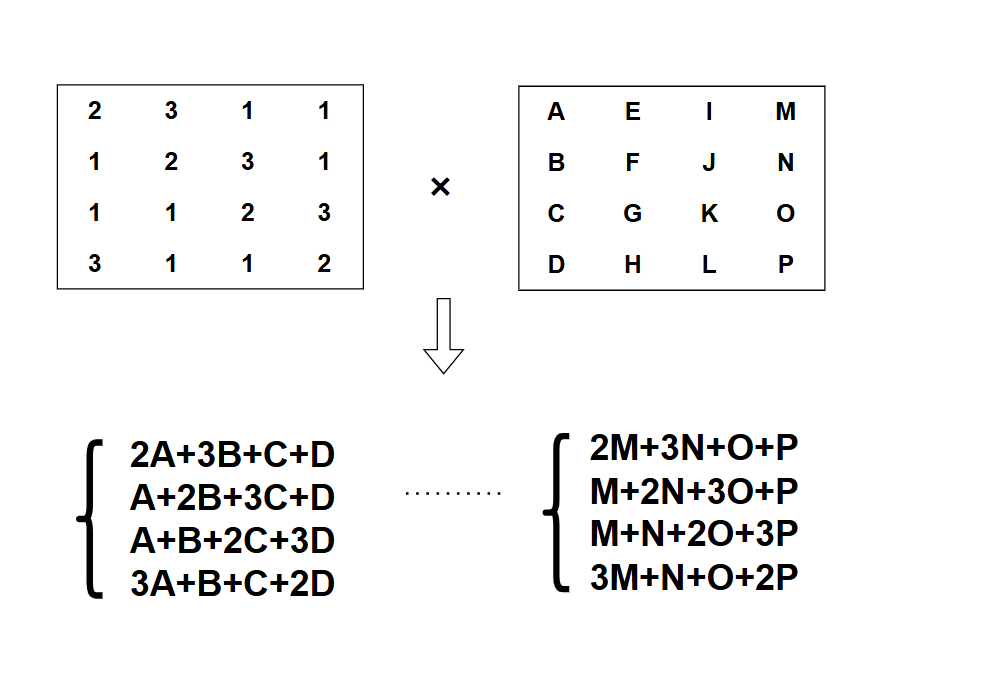
image-20251115212809826

在AES算法中加法就是异或，因此式子就变为

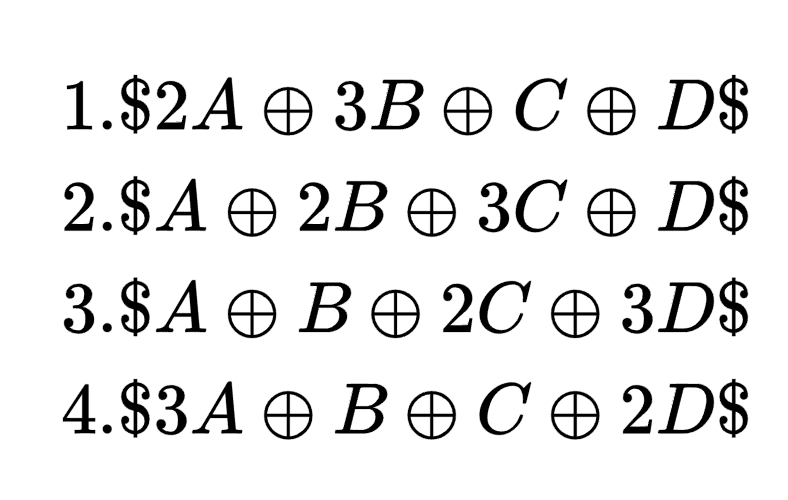
image-20251118104534589

其中乘法是伽罗瓦域内乘法($GF(2^8)$)，根据上述的式子由三种情况，$1A$、$2A$、以及$3*A$

  • $1*A = A$

  • $2*A$，则是将$A << 1$，但是需要判断左移后是否有溢出发生，若发生溢出还需要加上0x1b

  • $3A = 2A + A$

在tiny-AES-c中实现的列混淆如下所示，首先xtime为二倍乘的实现，首先判断是否有溢出发生，若有则异或0x1b，反之则不用。

【----帮助网安学习，以下所有学习资料免费领！加vx：YJ-2021-1，备注 “博客园” 获取！】

　① 网安学习成长路径思维导图
　② 60+网安经典常用工具包
　③ 100+SRC漏洞分析报告
　④ 150+网安攻防实战技术电子书
　⑤ 最权威CISSP 认证考试指南+题库
　⑥ 超1800页CTF实战技巧手册
　⑦ 最新网安大厂面试题合集（含答案）
　⑧ APP客户端安全检测指南（安卓+IOS）

在具体的列混淆中有一个便捷操作就是先计算出

image-20251118104558320

这是因为每一次的列混淆都需要计算该值，因此提前计算避免重复操作，这里以

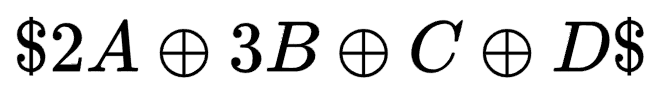
image-20251118104616288

为例。

image-20251118104642152

因此列混淆的计算可以化简三个部分

  • 二倍乘的计算

  • 公共部分的计算

  • 自身值

//xtime为GF(2^8)的二倍乘
static uint8_t xtime(uint8_t x)
{
  //左移一位相当于乘以2，然后右移7位判断最高位是否位1，为1就需要异或0x1b，否则不用
  //最高位为1，左移会溢出，因此需要加上0x1b，再GF(2^8)中加法等于异或
  return ((x<<1) ^ (((x>>7) & 1) * 0x1b));
}
​
// MixColumns function mixes the columns of the state matrix
static void MixColumns(state_t* state)
{
  uint8_t i;
  uint8_t Tmp, Tm, t;
  for (i = 0; i < 4; ++i)
  {  
    //t是A
    t   = (*state)[i][0];
    //先求a[0]^a[1]^a[2]^a[3]，因为这是求解的公共部分，避免重复操作
    Tmp = (*state)[i][0] ^ (*state)[i][1] ^ (*state)[i][2] ^ (*state)[i][3] ;
    //2A+3B+C+D = 2A+2B+B+C+D = 2*(A+B)+B+C+D = 2*(A+B)+(A+B+C+D)+A 
    Tm  = (*state)[i][0] ^ (*state)[i][1] ; Tm = xtime(Tm);  (*state)[i][0] ^= Tm ^ Tmp ;
    //A+2B+3C+D
    Tm  = (*state)[i][1] ^ (*state)[i][2] ; Tm = xtime(Tm);  (*state)[i][1] ^= Tm ^ Tmp ;
    //A+B+2C+3D
    Tm  = (*state)[i][2] ^ (*state)[i][3] ; Tm = xtime(Tm);  (*state)[i][2] ^= Tm ^ Tmp ;
    //3A+B+C+2D
    Tm  = (*state)[i][3] ^ t ;              Tm = xtime(Tm);  (*state)[i][3] ^= Tm ^ Tmp ;
  }
}

逆向中AES的识别

这里以[SCTF2019]creakme为例，从ida的反编译中识别AES算法

密钥扩展

首先在看到一串明文字符时，可以根据该字符串长度去判断是否为密钥以及AES算法的种类，下图中存在着字符串sycloversyclover，该字符串的长度为16，以及有字符串拆分成字节的形式进行存储，根据tiny-AES-c源码分析可知，在实际操作中，需要将密钥以字节的形式进行操作，因此根据长度以及字节存储的操作，可以猜测此算法可能为AES-128，该字符串为密钥。

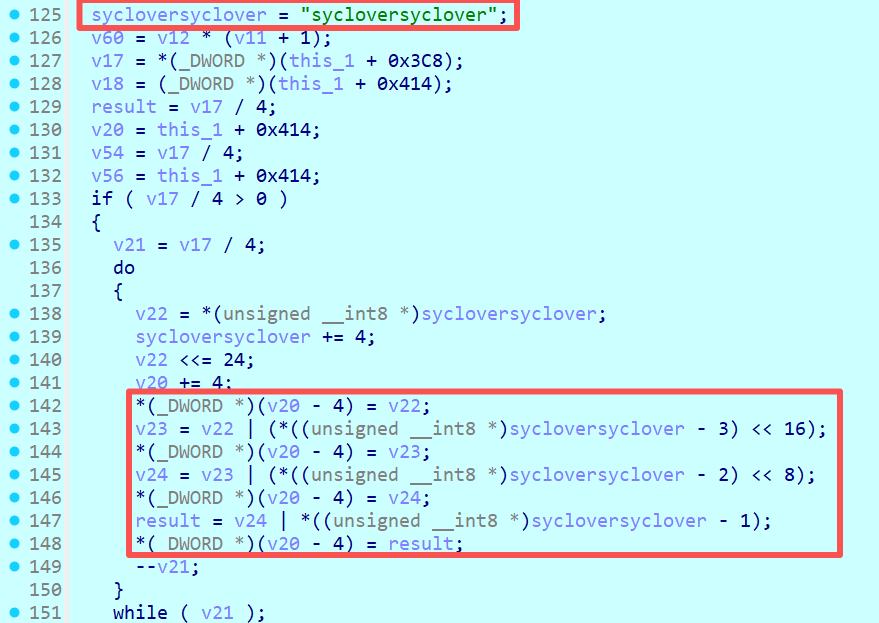
image-20251115215546915

在结合下述操作可以发现，在代码185行中具有S盒替换（S_BOX[v31]）、行位移（<<8），可以看到在ida的反编译中会将G运算集成在一步中。

image-20251115220210972

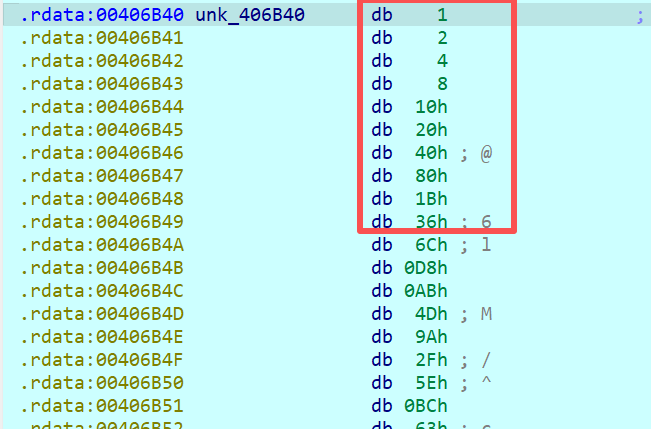
那么G运算中还存在一个常量异或的操作，因此*v32大概率是取出Rcon数组值的操作，而v32由v59赋值而来，v59又由unk_406B40赋值而来，那么查看unk_406B40的值，确实是Rcon数组值一致，验证了该算法就是AES算法，并且该函数是密钥扩展的操作。

image-20251115220618246

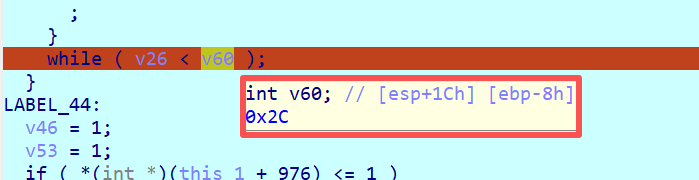
那么还有一个关键点可以分析，那就是循环的次数，由于密钥扩展需要扩展到$k_{44}$，因此循环的下标最大值也为44，循环次数也能对上。

image-20251115220724617

加密阶段

在加密阶段实际上可以直接看最后一轮，因为最后一轮的加密操作中是不需要进行列混淆的，如下图所示进行很明显进行了S盒替换与轮密钥加，这里可能大家疑惑，那行位移去哪里了？仔细看，实际上每次进行S盒替换的变量是不一样的，分别是v21、v5、v23以及v24我在图中给大家标记出来，而上述这些变量都是int类型的，实际上就是每次都存储4字节，那么就相当于按行存储了，在AES算法浅析部分跟大家分析过，若是按行存储的，那么就列往上移动即可，所以第二次的顺序就变成了v5、v23、v24、v21了。

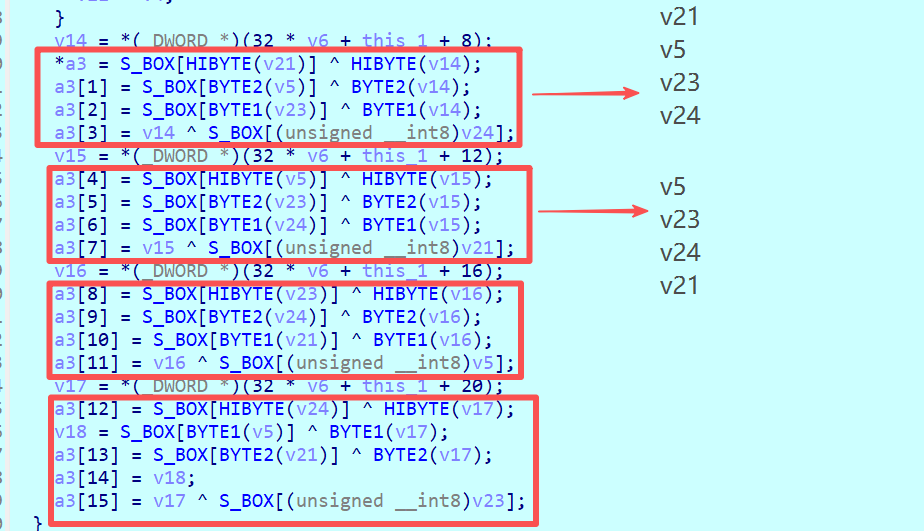
image-20251115221637087

那么说明上面的部分实际上就增加列混淆的操作，但是这部分操作确实是有字节替换，但是好像替换的数据并不是S盒？

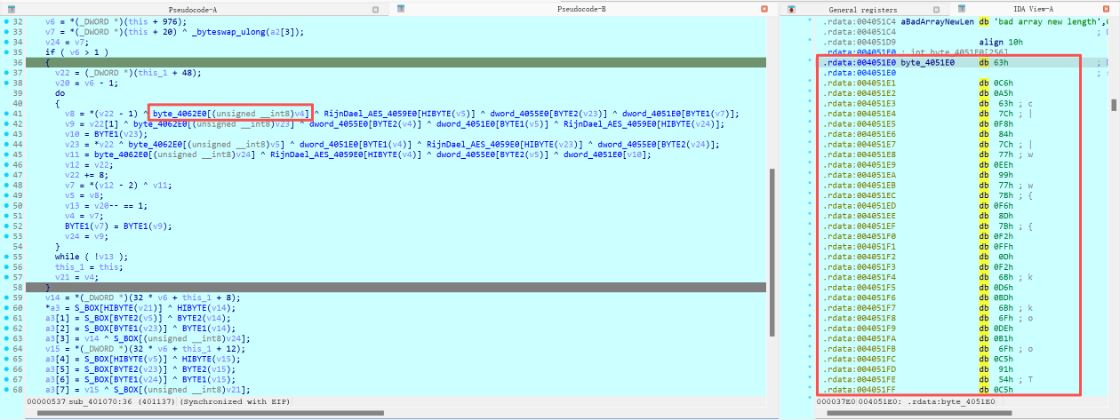
image-20251115222147517

实际上这是AES算法以空间换时间的实现，即T盒（T-table)实现。在上述提到的实现中，是首先将明文输入->轮密钥加->s盒替换->行位移->列混淆，这些操作实际上都是以字节为单位进行运算的，字节之间是不会相互影响的，那么一个字节的范围为0-255，将该范围的所有情况进行s盒替换->行位移->列混淆的结果先计算好，并将该结果集称之为T盒（T-table），那么当输入一个明文字节时，只需要做一个T盒的替换就可以立刻得到上述过程的结果，极大节约了运算的时间。因此这也是为啥替换的表不是S盒的原因。

那么而根据上述分析可以得出该函数为加密阶段函数。

加密模式

实际上在分析出密钥扩展或加密阶段的操作之后都可以比较明确的分析出该程序使用的算法了，但是为什么还是最好能够快速区分出这两个阶段呢？因为对称加密还存在加密模式，如ECB、CBC、CFB等，可以看到在加密阶段之前会与v15进行异或，那么可以猜测为CBC的加密模式，那么就需要找IV初始向量值。

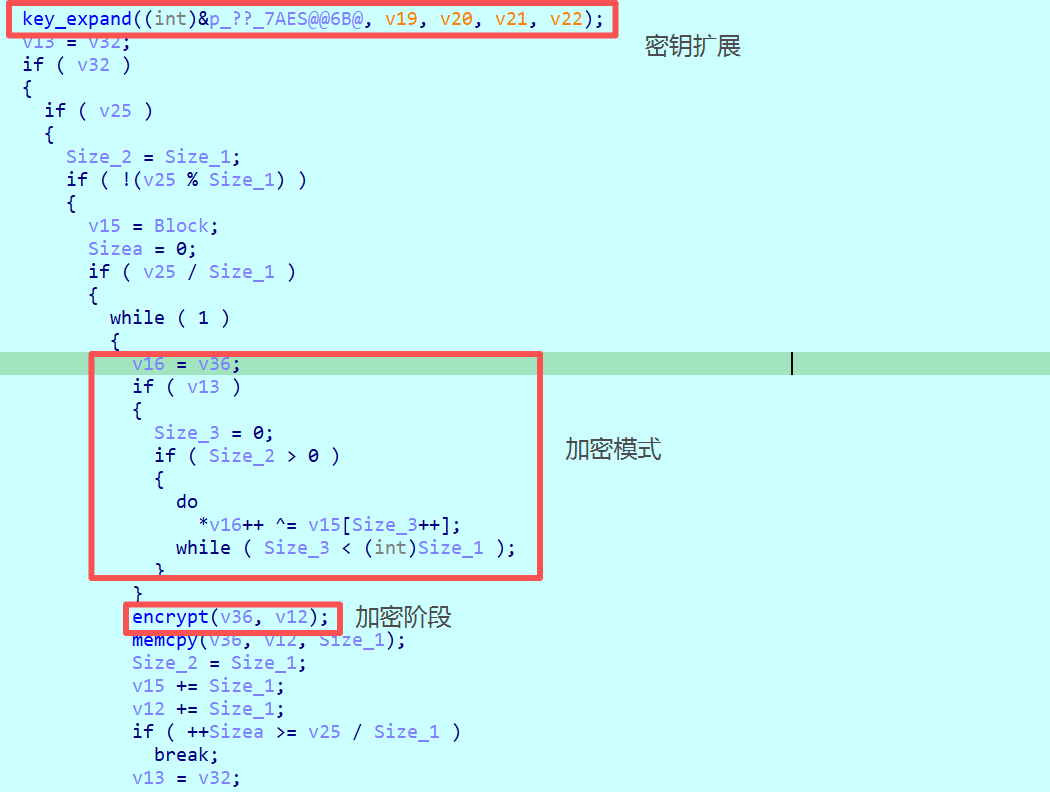
image-20251115223423002

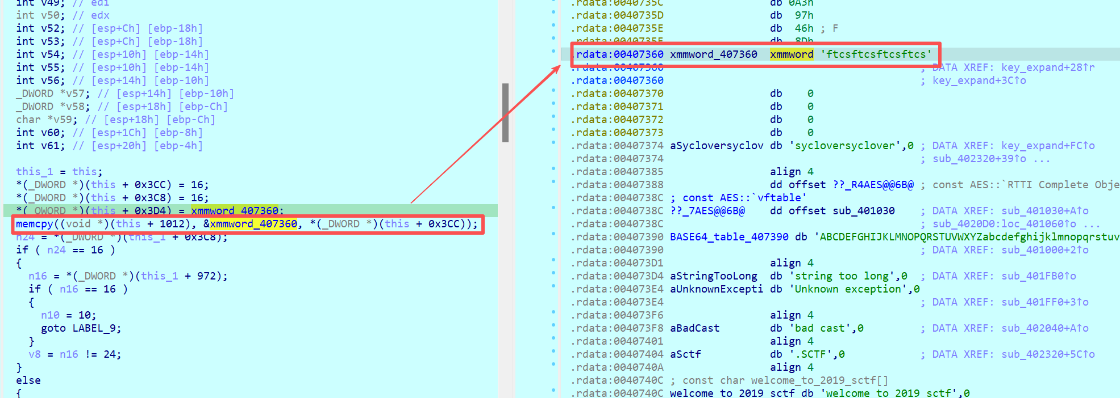
在密钥扩展期间还存在IV向量的拷贝过程，因此也验证了上述猜测的CBC加密模式。

image-20251115223547789

总结

AES算法是常见的对称加密算法，若熟悉其中的加密流程，也可以极大节约逆向的时间。

识别AES算法可以通过下述条件进行大致分析

  • 密钥扩展的循环次数

  • S盒

  • 第十轮的加密流程

参考连接

白盒AES算法详解(一)：https://bbs.kanxue.com/thread-280335.htm

tiny-AES-c：https://github.com/kokke/tiny-AES-c

 

更多网安技能的在线实操练习，请点击这里>>

posted @ 2025-12-09 14:32  蚁景网安实验室  阅读(6)  评论(0)    收藏  举报