二维几何基础
计算几何中坐标一般是实数,编程时使用double,不要使用精度较低的float。
在进行浮点数运算时会产生精度误差,可以设置一个偏差值eps(epsilon)来控制精度。
判断浮点数是否等于零或两个浮点数是否相等要用eps辅助判断。
#include<bits/stdc++.h>
using namespace std;
#define db double
const db pi = acos(-1.0); //高精度圆周率
const db eps = 1e-8; //可根据具体需要更改精度
inline int sgn(db x){ //判断是否等于零
if(fabs(x)<eps) return 0;
else return x<0?-1:1;
}
inline int dcmp(db x,db y){ //比较浮点数
if(fabs(x-y)<eps)return 0;
else return x<y?-1:1;
}
点和向量
1.点
二位平面中的点用(x,y)表示。
struct Point{
db x,y;
Point(){}
Point(db _x,db _y):x(_x),y(_y){}
};
2.两点之间的距离
db Dist(Point &a,Point &b){
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
3.向量
有大小,有方向的量称为向量(矢量) ,只有大小没有方向的量称为标量。
在平面上两个点可确定一个向量,由于向量不是一个有向线段,及向量没有起点与终点的概念,所有向量平移后不变。大多时候为了方便可直接将向量平移到原点处。向量的表示在形式上与点一样,可以用点的数据结构表示向量。
typedef Point Vector;
4.向量的运算
在struct Point中,对向量运算重载运算符。
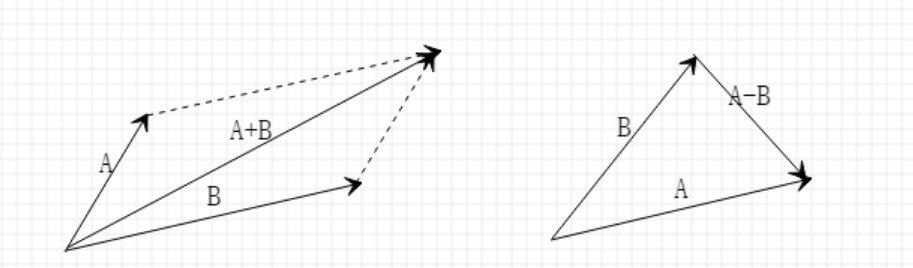
+:点加点没有意义,点加向量得到另一个点,向量加向量得到另一个向量。
Point operator+(Point &a){return Point(x+a.x,y+a.y);}
-:两个点的差得到一个向量,向量A减B得到有B指向A的向量。
Point operator-(Point &a){return Point(x-a.x,y-a.y);}
*:向量乘实数等比例放大。
Point operator*(db a){return Point(x*a,y*a);}
/:向量与实数相除等比例缩小。
Point operator/(db a){return Point(x/a,y/a);}
==:相等
bool operator==(Point &a){return sgn(x-a.x)==0&&sgn(y-a.y)==0;}
点积和叉积
向量的基本运算是点积和叉积,计算几何的各种操作几乎都基于这两种操作。
1.点积(Dot product)
$$A\cdot B = |A||B|cos\theta$$
其中\(\theta\)为A,B之间的夹角。点积的几何意义是A在B上投影的长度乘以B的模长。
在编程中并不需要知道\(\theta\)。如果已知\(A = (A.x,A.y),B = (B.x,B.y)\),那么有:
\(A\cdot B = A.x*B.x+A.y*B.y\)
\(A.x*B.x+A.y*B.y\)
\(=(|A|cos\theta 1*|B|cos\theta 2)+(|A|sin\theta 1*|B|sin\theta 2)\)
\(|A||B|(cos\theta 1cos\theta 2+sin\theta 1sin\theta 2)\)
\(|A||B|cos(\theta 1-\theta 2)\)
$|A||B|cos\theta $
db Dot(Vector &a,Vector &b){return a.x*b.x+a.y*b.y;}
2.点积的应用
1)判断A,B之间的角是钝角锐角还是直角。
2)求A的长度(模)
db len(Vector &a){return sqrt(Dot(a,a));}
3)求A,B夹角的大小
db Angle(Vector &a,Vector &b){return acos(Dot(a,b)/len(a)/len(b));}
3.叉积(Cross product)
叉积是比点积等常用的集合概念。
\(\theta\) 表示A旋转到B所经过的夹角。
两个向量的叉积的结果是一个带符号的数值,其几何意义为A,B形成平行四边形的“有向”面积,其正负可通过“右手定则”判断。
db Cross(Vector &a,Vector &b){return a.x*b.y-a.y*b.x;}
\(A.x*B.y-A.y*B.x\)
=\(|A||B|(cos\theta 1sin\theta 2-sin\theta 1cos\theta 2)\)
=\(|A||B|sin(\theta 2-\theta 1)\)
当\(\theta 2\)>\(\theta 1\)时,结果为正,且B在A的逆时针方向。
故可通过正负来判断A,B的相对位置。
4.叉积的基本应用
1)判断A,B的方向关系。
2)计算两向量构成的平行四边形的“有向面积”
db Area2(Point a,Point b,Point c){return Cross(b-a,c-a);}
3)计算3个点构成的三角形面积
4)向量旋转
是向量(x,y)绕起点逆时针旋转\(\theta\),旋转后的向量为(\(x^{\prime}\),\(y^{\prime}\))
Vector Rotate(Vector a,db rad){
return Vector(a.x*cos(rad)-a.y*sin(rad),a.x*sin(rad)+a.y*cos(rad));
}
5)用叉积检查向量是否平行或重合
bool Parallel(Vector a,Vector b){return sgn(Cross(a,b))==0;}
点和线
1.直线的表示
直线的表示方法很多,编程时可灵活选择:
1)用直线上的两个点表示。
2)\(ax+by+c = 0\),普通式。
3)\(y = kx+b\),斜截式,注意斜率不存在的情况。
4)\(P = P_0+vt\),点向式。用\(P_0\)和\(v\)来表示直线\(P\),\(t\)是任意值,\(P_0\)是直线上一点,\(v\)是方向向量,\(v=A-B\)。
t无限制时,P是直线。
t\(\in\)[0,1],P是A,B之间的线段。
t>0,P是射线。
struct line{
Point p1,p2;
line(){}
line(Point _p1,Point _p2):p1(_p1),p2(_p2){}
//一个点和角(angle)确定直线,0<=angle<pi
line(Point p,db angle){
p1=p;
if(sgn(angle-pi/2)==0){p2=p+Point(0,1);}
else p2=p+Point(1,tan(angle));
}
//ax+by+c=0;
line(db a,db b,db c){
if(sgn(a)==0){
p1=Point(0,-c/b);
p2=Point(1,-c/b);
}
else if(sgn(b)==0){
p1=Point(-c/a,0);
p2=Point(-c/a,1);
}
else{
p1=Point(0,-c/b);
p2=Point(-c/a,0);
}
}
};
2.线段的表示
可以用两个点表示线段,直接用直线的数据结构表示线段。
typedef line Segment;
3.在二维平面上,点和直线有三种位置关系,在直线上,左侧和右侧。用叉积的正负可判断方向。
int Point_line_relation(Point p,line v){
int c=sgn(Cross(p-v.p1,v.p2-v.p1));
if(c<0)return 1; //顺时针
else if(c>0)return 2; //逆时针
return 0; //在直线上
}
4.点和线段的关系
先用叉积判断是否共线,再用点积判断点与线段两端的角是否为\(180^°\)。
int Point_on_seg(Point p,line v){
return sgn(Cross(v.p1-p,v.p2-p))==0&&sgn(Dot(v.p1-p,v.p2-p))<=0;
}
5.点到直线的距离
已知点\(p\)到直线\(v(p_1,p_2)\),求\(p\)到\(v\)的距离。首先用叉积求\(p,p_1,p_2\)构成的平行四边形的面积,然后除以线段\((p_1,p_2)\)的长度即可。
db Dis_point_line(Point p,line v){
return fabs(Cross(p-v.p1,v.p2-v.p1)/Dist(v.p1,v.p2));//注意叉积有正负
}
6.点在直线上的投影
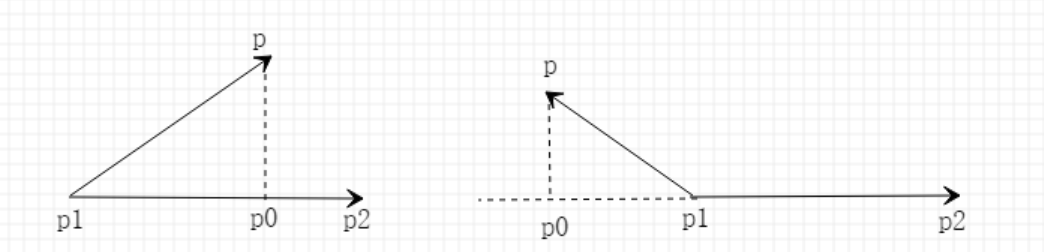
已知直线上的两点\(p_1,p_2\)以及直线外一点\(p\),求投影点\(p_0\),我们先来看下上图左边的那种情形。
令\(k=\frac{|p_0-p_1|}{|p_2-p_1|}\),即k是线段\(p_0p_1\)和\(p_2p_1\)长度的比值,那么有\(p_0=p_1+k*(p_2-p_1)\)。
根据点积的概念有,
\((p-p_1)\cdot(p_2-p_1)=|p_0-p_1|*|p_2-p_1|\)
及\(|p_0-p_1|=\frac{(p-p_1)\cdot(p_2-p_1)}{|p_2-p_1|}\)
带入即:
\(k=\frac{|p_0-p_1|}{|p_2-p_1|}=\frac{(p-p_1)\cdot(p_2-p_1)}{|p_2-p_1|*|p_2-p_1|}\)
那么:
\(p_0=p_1+\frac{(p-p_1)\cdot(p_2-p_1)}{|p_2-p_1|*|p_2-p_1|}*(p_2-p_1)\)
容易证明上图右边那种情况也满足此式。
Point Point_line_proj(Point p,line v){
double k=Dot(p-v.p1,v.p2-p)/len(v.p2-v.p1)/len(v.p2-v.p1);
return v.p1+(v.p2-v.p1)*k;
}
7.点关于直线的对称点
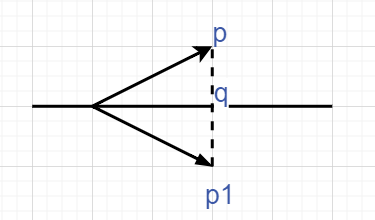
求点p关于直线的对称点,先求投影点,在求对称点。
Point Point_line_symmetry(Point p,line v){
Point p1=Point_line_proj(p,v);
return Point(p1.x*2-p.x,p1.y*2-p.y);
}
8.点到线段的距离
点p到线段AB的距离,在p到A的距离,p到B的距离,p到直线AB的距离(如果垂足在线段AB上)。
db Dis_point_seg(Point p,Segment v){
if(Dot(p-v.p1,v.p2-v.p1)<0||Dot(p-v.p2,v.p1-v.p2)<0)return min(Dist(p,v.p1),Dist(p,v.p2));
return Dis_point_line(p,v);
}
9.两条直线的位置关系
叉积 啪 的一下就出来了
int line_relation(line v1,line v2){
if(sgn(Cross(v1.p1-v1.p2,v2.p1-v2.p2))==0){
if(Point_line_relation(v1.p1,v2)==0)return 1;//重合
else return 0;//平行
}
return 2;//相交
}
10.求两个直线的交点
可以联立方程求解,也可以用简单的叉积来实现。
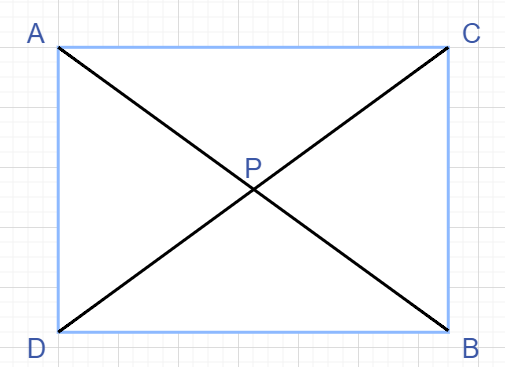
为了方便图画成长方形了,不要被带偏了。。。。
如图,AB与CD的交点为P。
容易得到以下两个等式:
\(\frac{|DP|}{|CP|}=\frac{S_{\bigtriangleup ABD}}{S_{\bigtriangleup ABC}}=\frac{\vec{AB}\times\vec{AD}}{\vec{AB}\times\vec{AC}}\)
\(\frac{|DP|}{|CP|}=\frac{x_D-x_P}{x_P-x_C}=\frac{y_D-y_P}{y_P-y_C}\)
联立上面两个方程,即可得到点P的坐标:
\(x_P = \frac{S_{\bigtriangleup ABD}\ \ \ \times x_C + S_{\bigtriangleup ABC }\ \ \ \times x_D}{S_{\bigtriangleup ABD}\ \ \ + S_{\bigtriangleup ABC}}\)
\(y_P = \frac{S_{\bigtriangleup ABD}\ \ \ \times y_C + S_{\bigtriangleup ABC }\ \ \ \times y_D}{S_{\bigtriangleup ABD}\ \ \ + S_{\bigtriangleup ABC}}\)
Point Cross_point(line a,line b){
db s1=Cross(b.p1-a.p1,a.p2-a.p1);
db s2=Cross(a.p2-a.p1,b.p2-a.p1);//注意叉积的正负
return Point(s1*b.p2.x+s2*b.p1.x,s1*b.p2.y+s2*b.p1.y)/(s1*s2);
}
注意函数要对(s1+s2)做除法,在调用前要保证两直线不平行且不重合。
11.判断两线段是否有交点
叉积 啪啪 两下就出来了。
bool Cross_segment(Segment a,Segment b){
db c1=Cross(a.p1-a.p2,b.p1-a.p2),c2=Cross(a.p1-a.p2,b.p2-a.p2);
db d1=Cross(b.p1-b.p2,a.p1-b.p2),d2=Cross(b.p1-b.p2,a.p2-b.p2);
return c1*c2<=0&&d1*d2<=0;
}
12.求两个线段的交点
先判断有没有交点,有交点转化为直线求就行了。
多边形
1.判断点在多边形内部
给定一个点P和一个多边形,判断点P在多边形的内部还是外部。
从点P引出一条直线(与多边形交于两点),检查P与多边形每条边的相交情况,检查的方向不影响结果,但不能中途改变方向。
检查以下3个参数:
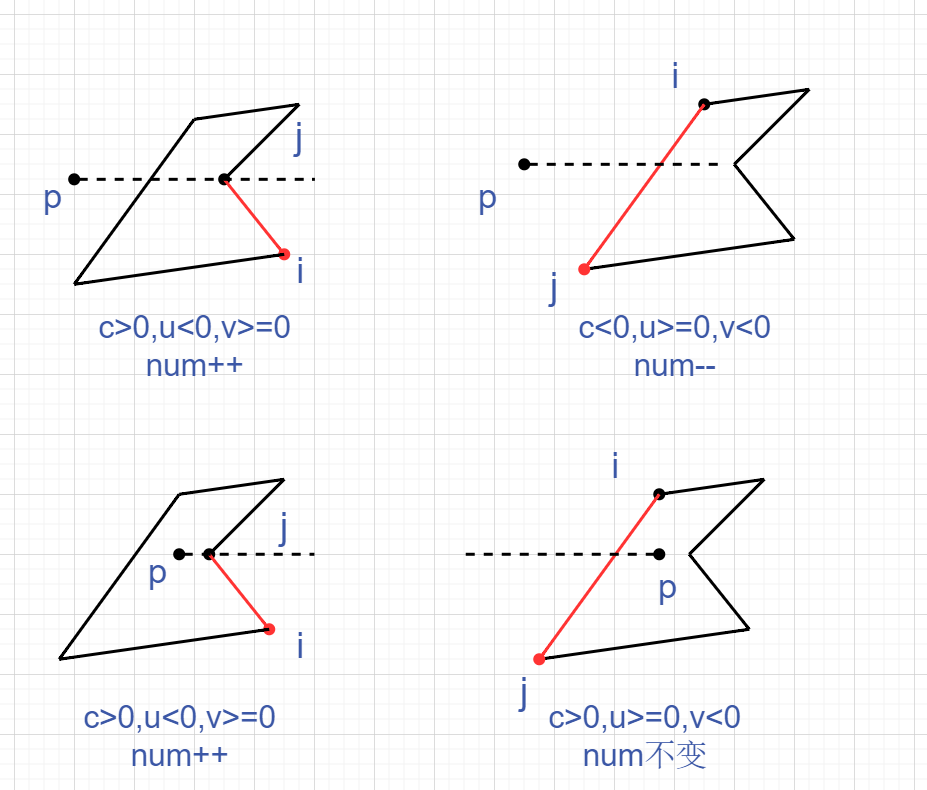
显然u,v是用来判断是否相交,c用来判断p与边的位置关系。
最后当num>0时p在多边形内部。
int Point_in_polygon(Point pt,Point *p,int n){
//注意P[]中的点为严格逆时针或顺时针
for(int i=0;i<n;++i){
if(p[i]==pt)return 3;//点p在多边形的顶点上
}
for(int i=0;i<n;++i){
line v=line(p[i],p[(i+1)%n]);
if(Point_on_seg(pt,v))return 2;//点在多边形边上
}
int num=0;
for(int i=0;i<n;++i){
int j=(i+1)%n;
int c=sgn(Cross(pt-p[j],p[i]-p[j]));
int u=sgn(p[i].y-pt.y);
int v=sgn(p[j].y-pt.y);
if(c>0&&u<0&&v>=0)num++;
if(c<0&&u>=0&&v<0)num--;//注意这里不能用n*v<0判断
}
return num>0;//1在内部,0在外部
}
3.求多边形面积
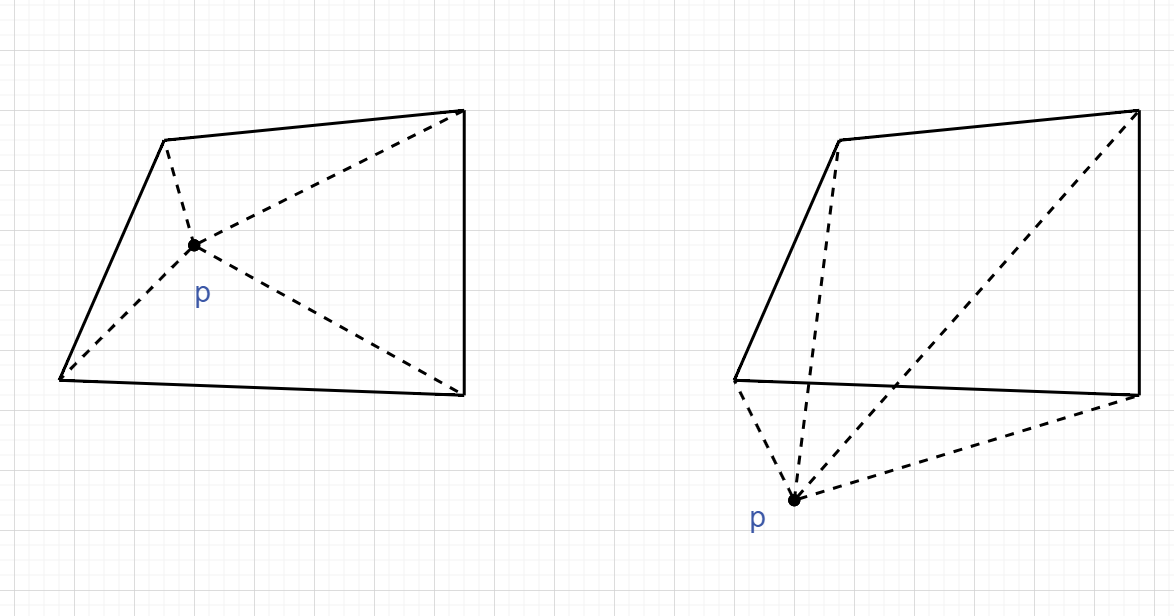
对于一个多边形,可以在其内部找一点p,将多边形划分为n个三角形,计算n个三角形的面积之和即可。
实际上p的位置可任意选取,叉积的正负可将多余的面积抵消掉,所以一般将p选在原点。
db Polygon_area(Point*p,int n){
db ans=0;
for(int i=0;i<n;++i){
ans+=Cross(p[i],p[(i+1)/n]);
}
return ans/2;//注意面积有正负,可根据需要判断是否要去绝对值
}
凸包
凸包问题:给定一些点,求能把所有这些点包含在内的面积最小的多边形。
Graham扫描发变种—————Andrew算法。先从最左边的点沿"下凸包"扫描到最右边再从最右边的点沿"上凸包"扫描到最左边,合起来就是完整的凸包。
具体步骤如下:
1)把所有点按照横坐标x从小到大进行排序,如果x相同,按y从小到大排序,并删除重复的点,得到序列\(\{p_0,p_1,p_2,\cdots,p_m\}\)。
2)从左到右扫描所有点,求"下凸包"。\(p_0\)一定在凸包上,从\(p_0\)开始,依次检查\(\{p_1,p_2,\cdots,p_m\}\),扩展出"下凸包"。判断依据是:如果新点在凸包"前进"方向的左边,说明可能在"下凸包"上,先加入到凸包中;如果在右边,说明拐弯了,删除最近加入下凸包的点。持续这个过程到检查完所有的点,拐弯方向用叉积判断。
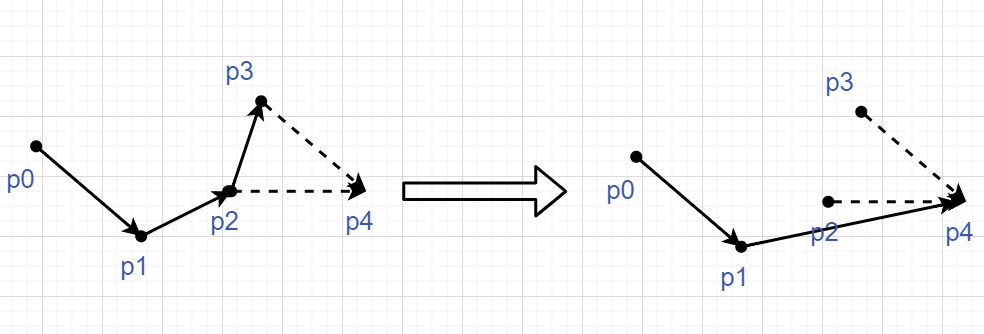
在检查\(p_4\)的时候发现\(p_4p_3\)对\(p_3p_2\)是右拐弯的,删除\(p_3\),退回\(p_2\),发现\(p_4p_2\)对\(p_2p_1\)也是有拐弯的,退回\(p_1\)。
3)从右到左重新扫描所有点,求"上凸包"。和求"下凸包"的过程类似,最右边的点\(p_m\)一定在凸包上。
复杂度:排序算法\(O(nlog_2n)\),扫描\(O(n)\),总复杂度\(O(nlog_2n)\)。
int Convex_hull(Point *p,int n,Point *ch){//求凸包
sort(p,p+n);
n=unique(p,p+n)-p;//去重 返回值是个迭代器,指向新容器的最后一个元素的下一个
int v=0;
//求下凸包
for(int i=0;i<n;++i){
while(v>1&&sgn(Cross(ch[v-1]-ch[v-2],p[i]-ch[v-2]))<=0)--v;
ch[v++]=p[i];
}
int j=v;
//求上凸包
for(int i=n-2;i>=0;--i){
while(v>j&&sgn(Cross(ch[v-1]-ch[v-2],p[i]-ch[v-2]))<=0)--v;
ch[v++]=p[i];
}
if(n>1)--v;//注意p0记录了两次
return v;//返回凸包的顶点数
}
最近点对
这里给一个\(O(nlog_2n)\)的分治法
#include<bits/stdc++.h>
using namespace std;
#define db double
struct point{
db x,y;
bool operator<(point a){
return x<a.x;
}
point(){}
point(db a,db b):x(a),y(b){}
};
#define Iter vector<point>::iterator
vector < point > node;
int n;
db dis(point a,point b){
return sqrt((pow(a.x-b.x,2)+pow(a.y-b.y,2)));
}
bool cmpy(point a,point b){
return a.y<b.y;
}
void sol(Iter l,Iter r,db &d){
if(r-l<=1)return;
vector<point> temp;
Iter mid=l+(r-l)/2;
db w=(*(l+(r-l)/2)).x;
sol(l,mid,d);sol(mid,r,d);
inplace_merge(l,mid,r,cmpy);
for(Iter t=l;t!=r;++t){
if(fabs(t->x-w)<d)temp.push_back(*t);
}
for(Iter t=temp.begin();t!=temp.end();++t)
for(Iter tt=t+1;tt!=temp.end()&&tt->y-t->y<d;++tt)
d=min(d,dis(*tt,*t));
}
int main(){
scanf("%d",&n);
db a,b;
for(int i=0;i<n;++i){
scanf("%lf%lf",&a,&b);
node.push_back(point(a,b));
}
db ans=1e18;
sort(node.begin(),node.end());
sol(node.begin(),node.end(),ans);
printf("%.0f",ans*ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号