根轨迹相角条件入射角和出射角的计算问题

在学习根轨迹的绘制时，我发现许多教材和资料对于相角条件和入射角、出射角的计算讲解较为笼统，只是给出了相关的公式，这样对于我们的理解往往会造成比较大的困难。

一些关于复数的数学基础

考虑复数z

\[z=a+bi=r(cos\theta+isin\theta)=re^{i\theta} \]

其中\(\theta\)被称为相角，r被称为幅值，这样将实部虚部转化为相角形式。

在实轴虚轴坐标系中，\(\theta\)可以表示为点与原点连线与实轴正半轴的交点。

考虑复数\(z_1,z_2\)

\[z_1z_2=re^{i(\theta_1+\theta_2)} \]

所以两个复数相乘等价于两者的相角相加，同理

\[z_1/z_2=re^{i(\theta_1-\theta_2)} \]

两个复数相减等于相角之差

同时

\[z_1-z_2=(a_1-a_2)+(b_1-b_2)i \]

对应的坐标\((a_1-a_2,b_1-b_2)\)，故\(\angle (z_1-z_2)\)可以理解为\(z_1,z_2\)两个复数在坐标系中对应点的连线与实轴正半轴的交点。

相角条件

考虑系统

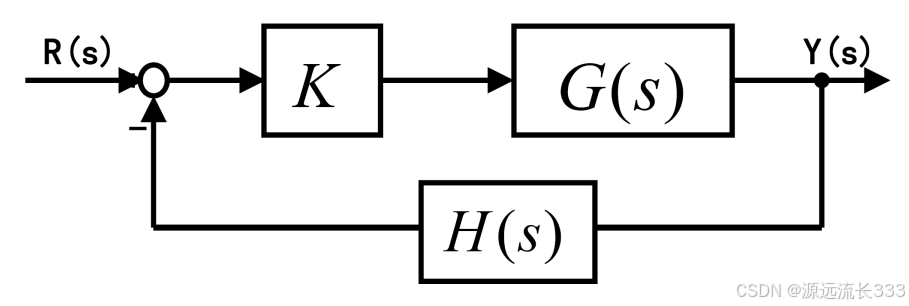
特征方程为

\[1+KG(s)H(s)=0 \]

那么

\[KG(s)H(s)=-1 \]

-1在复数域对应的相角为\((2k+1）\pi\)，所以我们能得到相角条件

\[\angle KG(s)H(s)=180^\circ+k360^\circ \]

ps.(k=0,1,2,3......n-m-1)
而且考虑到

\[KG(s)H(s)=\frac{K(s+z_1)(s+z_2)...(s+z_m)}{(s+p_1)(s+p_2)...(s+p_n)} \]

其中z为零点，p为极点，考虑到复数相除等于相角相减，所以

\[\angle KG(s)H(s)=\angle (s-z_1)+\angle (s-z_2)+...+\angle (s-z_m)-\angle (s-p_1)-\angle (s-p_2)...-\angle(s-p_n) \]

即

\[\angle KG(s)H(s)=\sum \phi_j-\sum \theta_i=180^\circ+k360^\circ \]

用通俗的语言来说，就是根轨迹上的点与零点连线的相角之和减去与极点相角之和等于\(\pi+2k\pi\)

出射角与入射角

现代控制理论书中对出射角的定义是出射角等于相角差的主值，但这个定义显然很难理解。

出射角可以简单理解为极点处切线与实轴正半轴夹角的值（可以类比为实值函数的导数qwq）。

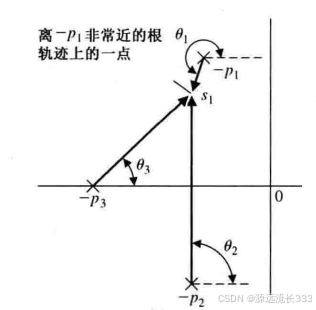
假设我们想要求\(p_1\)处对应的出射角，我们在根轨迹上取一个无限接近于\(p_1\)的点\(s_1\)，这样根轨迹在\(p_1\)处切线的角度\(\theta_1\)课等效为\(p_1,s_1\)连线与实轴正半轴的夹角，即

\[\angle (s_1-p_1)=\theta_1 \]

我们考虑到\(s_1\)在根轨迹上，考虑相角条件

\[\angle (s_1-z_1)+\angle (s_1-z_2)+...+\angle (s_1-z_m)-\angle (s_1-p_1)-\angle (s_1-p_2)...-\angle(s_1-p_n)=(2k+1)\pi \]

所以

\[\angle(s_1-p_1)=-(2k+1)\pi+\sum_{j=1}^m(s_1-z_j)-\sum_{i=1,i\neq1}^n(s_1-p_i) \]

考虑\(s_1\)无限接近于\(p_1\)，将上式右边的\(s_1\)替换为\(p_1\)，得

\[\angle(s_1-p_1)=-(2k+1)\pi+\sum_{j=1}^m(p_1-z_j)-\sum_{i=1,i\neq1}^n(p_1-p_i) \]

将\(p_1\)替换为更为普遍的\(p_r\)，同时对\(-(2k+1)\pi\)（k=0,1,2...）进行调整，得到出射角

\[\theta_r=(2k+1)\pi+\sum_{j=1}^m(p_r-z_j)-\sum_{i=1,i\neq r}^n(p_r-p_i) \]

其中\(k=0,\pm1,\pm2...\)

同理，我们也可以得到入射角

\[\phi_r=(2k+1)\pi-\sum_{j=1,j\neq r}^m(z_r-z_j)+\sum_{i=1}^n(z_r-p_i) \]

参考资料

南京大学控制理论课程

现代控制理论，第十二版

如有错误请指正