记录
写这个是因为 NOIP2024 剩百日,这他妈是最后一次了,就让我拿个一等吧,别无所求了。
把之前做过的题都重新总结一遍,怎么说也都能吃透了。
P6880 JOI 2020 Final] オリンピックバス
给一个有向图,经过边有代价 \(C_i\),可以反转某一条边,代价为 \(D_i\)。问从 \(1\) 到 \(n\) 再从 \(n\) 到 \(1\) 且最多反转一次边的最小代价和。
暴力想法是枚举翻转哪一条边然后重跑最短路。考虑翻转一条边产生的影响,令 \(f(s,t)\) 为原图上 \(s\) 到 \(t\) 的最短距离,翻转一条边之后 \(1\) 到 \(n\) 的最短路为 \(D1\),\(n\) 到 \(1\) 为 \(D2\)。
容易得出:\(D1=\min(f(1,n),f(1,v)+w+f(u,n)),D2=\min(f(n,1),f(n,v)+w+f(u,1))\)
然后需要知道一个性质:在图 \(G\) 上构造根为 \(x\) 的最短路树 \(T\),任意删除一条不在 \(T\) 上的边, \(x\) 到其他任意节点的距离不会发生变化。
那么也就是说对于不在最短路树上的边,反转这条边后的 \(1,n\) 到其两端点的最短路是不变的,也就不需要重新求最短路了。而在最短路树内的边最多只有 \(n-1\) 条,那么枚举到这些边时重跑最短路是完全没有问题的。
注意是稠密图考虑使用不加堆优化的dij;有重边所以判断一条边要记录编号;在求起点不是 \(1\) 或 \(n\) 的最短路时可以考虑在反图上以 \(1\) 或 \(n\) 为起点跑。
ABC264Ex Perfect Binary Tree
对于一棵树动态加点,求当前以 \(1\) 为根的满二叉树个数。
计数题考虑 dp。首先满二叉树树高最多 \(\log n\) ,所以只用考虑高度少于 \(\log n\) 的点。
设 \(dp_{x,dep}\) 表示以 \(x\) 为根,最大深度为 \(dep\) 的满二叉树个数。朴素转移即在两个层高为 \(dep-1\) 的满二叉树拼起来,即:\(dp[x][dep]=\sum\limits_{u<v,u,v\in son_x} dp[u][i-1]\times dp[v][i-1]\)
但因为是动态加点,所以这样转移复杂度会爆的。考虑将乘积式子拆开,根据完全平方公式可以化为:\(dp[x][dep]=\sum\limits_{u<v,u,v\in son_x} \frac{1}{2}((\sum\limits_{u\in son_x} dp[u][i-1])^2-(\sum\limits_{v\in son_x} dp[v][i-1])^2)\)
转移过程中维护和与平方和即可 \(O(1)\) 修改变化量,复杂度 \(O(n\log n)\)
CF452F Permutation
给你一个 \(1\) 到 \(n\) 的排列,你需要判断该排列内部是否存在一个 \(3\) 个元素的子序列(可以不连续),使得这个子序列是等差序列。
正解是线段树维护哈希,但是有奇妙性质:存在 \(3\) 个元素的等差序列时一定有其中点和左右两端的距离不超过 \(12\)。当然这个值肯定是和 \(n\) 相关的,但那篇论文着实让我看不出来。然后能过。
ABC329F Colored Ball
基础的启发式合并。我们对每个盒子开个 set 就行了,合并的时候就启发式合并,小的合并到大的上保证复杂度。
CF1898D Absolute Beauty
考虑将 \((a_i,b_i)\) 看作是一段区间,我们想要在一次操作内增加尽量多的长度,考虑分讨两端线段的相交情况,最后得出结论:选择最大的 \(l_i\) 和最小的 \(r_j\) 进行操作,可以使收益最大。
trick:类似于 \(|a_i-b_i|\) 的式子可以考虑转化为区间来分讨考虑。
P8386 & P10375
给定 \(n\),\(m\),求满足以下限制的长度为 \(n\) 的序列数目:
\(1.\) 每个元素在 \([1,m]\) 之间;
\(2.\) 一次操作定义为删除一个长度至少为 \(2\) 且区间两端相等的区间,该序列需要在若干次操作内被删空。
答案对 \(10^9+7\) 取模。
计数题,考虑dp。对于这种合法序列计数题,可以从在末尾新增一个数的情况入手,放在这个题中,发现对于一个序列 \(S\) 的某一项 \(x\),若其前缀是合法的,则 \(S+x\) 也是合法的(原因显然)。那么这样可以设出状态:\(dp[i][j][0/1]\) 表示填了前 \(i\) 个数的序列合法/不合法,\(i+1\) 位置填已经出现过的 \(j\) 种数的方案数。
根据状态设定,显然适合用填表法,转移要分讨一下,分当前是否合法,填的数是已经出现的 \(j\) 种还是其他 \(m-j\) 种:
(dp[i+1][j][1]+=dp[i][j][0]*j%mod)%=mod;
(dp[i+1][j][0]+=dp[i][j][0]*(m-j)%mod)%=mod;
(dp[i+1][j][1]+=dp[i][j][1]*j%mod)%=mod;
(dp[i+1][j+1][0]+=dp[i][j][1]*(m-j)%mod)%=mod;
P11013 「ALFR Round 4」C 粉碎
首先考虑记 \(las_i\) 为 \(a_i\) 上一次出现的位置。手玩可以发现最优方案一定是删除一段前缀,最后剩下来的一定都是单牌。那么也可以推断出我们只需要找到最后一个可被删掉的牌,并且这张牌一定是被匹配的一张牌。再思考一下,可以发现对于前 \(i\) 张牌,如果所有 \(las_i\) 前的所有 \(a_i\) 能被删完,那么 \([1,i]\) 就是能被删完的。
那么考虑设 \(dp[i]\) 表示是否能删完 \([1,i-1]\),如果 \(dp[las[i]]=1\) 那么 \([1,i]\) 就是能删完的。考虑转移,\(las_i\) 能被删掉有两种可能,一是与 \(las_{las_i}\) 匹配,二是被某一个 \(j\in(las_i,i)\) 和 \(las_j\) 匹配删掉了,转移综合起来就是 \(dp_[i]|=dp_{las_j},j\in[las_i,i)\)。
这仍然是 \(O(n^2)\) 的。观察式子,容易想到可以前缀和优化,令 \(sum_i=sum_{i-1}+dp_{las_i}\) 就行,因为转移也是从 \(las_i\) 处转移的,转移部分变成 \(dp_i=[sum_{las_i-1}<sum_{i-1}]\)。
P2446 SDOI2010 大陆争霸
想法比较自然。会想到对于点 \(u\),其解锁时间等于其前置节点的最大值 \(D\) 和自身的到达时间(不关心解锁)的较大值。那么可以直接跑一遍 dij 然后用拓扑排序的方式更新每个点的解锁时间,很简单。
然后你会发现只对了一个点,原因是你先直接跑 dij 可能会出现最短路上的点仍然未解锁的情况,感性理解容易发现这显然错了,所以要在跑 dij 的同时进行拓扑排序对解锁时间更新。注意更新解锁时间要多开一个数组。
UVA11987
直接无脑并查集是错的。有个trick:考虑对每个集合建一个虚点,每次合并时就把要合并的点连到对应集合的虚点上,虚点始终保持不动,这样子就对了。
[P1525 NOIP2010 提高组] 关押罪犯
带权并查集,判断关系时看两点权值差的奇偶性就行。
[P6061 加油武汉] 疫情调查
网络流会不了一点。
P11022
容易发现当图不联通或是一棵树时无解。考虑加入一条非树边形成一个环,一个简单的想法是将某个点染成白色其它点染成黑色。但是这样是能被hack掉的,考虑一条使得上述方案不合法的边 \((u,v)\),如果要使其合法可以将包含 \(u,v\) 的一部分点全染成白色,这样就合法了。
P8817 CSP-S 2022 假期计划
首先 \(O(n^2)\) 预处理全源最短路方便后续操作,bfs即可。考虑暴力一点的想法,直接枚举要到达的点,但是数据明显只允许暴力枚举两个点的组合。容易发现,只需要枚举 \(B,C\) 点即可,因为 \(A,D\) 点都有一个距离 \(1\) 号点距离 \(\le k\) 的限制,所以在确定下来 \(B,C\) 之后就可以跟着确定 \(A,D\)。但是满足限制的 \(A,D\) 可能很多,解决这个可以只考虑每个点能到达的最优点,但是因为选择的点不能重复,所以要至少保留三个最优的点,可以用set或堆维护。然后枚举一下点的组合就做完了。注意 \(k\) 要加一和开 long long。
P3537 POI2012 SZA-Cloakroom
数据范围看错了以为背包过不了( 首先询问离线下来是好想的,离线下来可以按 \(m\) 升序排序,同时对物品也按 \(a\) 升序排序。然后考虑怎么满足后两个限制,如果没有 \(b>m+s\) 的话就可以直接对 \(c\) 背包求能否凑出 \(k\)。有个trick:考虑将设状态为 \(dp[i]\) 表示物品的 \(c\) 之和为 \(i\) 的方案中最大的 \(b\) 最小值,只要这个尽量大的最小值 \(>m+s\) 那么这个方案就是合法的,也就是有解。然后做完了。
P8868 NOIP2022 比赛
首先 \(O(qn\log n)\) 的分治可以 52pts。继续考虑分治,优化的点在于每次询问都要重新分治一遍,自然会想到能不能一遍分治把所有询问搞完。如果要这样那么显然把询问离线,在分治过程中将每个区间的贡献加到包含它的询问中。
P4155 SCOI2015 国旗计划
在题目的限制下对每个人可以贪心地找到右端点最大的左端点被他包含的人,然后破环成链,倍增覆盖就行了。
ABC346G
给定一个长度为 \(n\) 的序列 \(A\),求其中有多少个子区间中至少有一个数字只出现过一次。
能想到的是计算每个数的贡献,这个数能贡献的区间显然是 \([l_i+1,r_i-1]\),贡献值为 \((i-l_i+1)\times(r_i-i+1)\)。但很明显这个区间内还会有别的数产生贡献,会算重。然后尝试把这个贡献变得形象,就会发现答案就是求 \(n\) 个左下角为 \((l_i,i)\) 右上角为 \((i,r_i)\) 的矩形的面积并,容易理解但不好想,想到了就直接扫描线就完了。
P9991 Ynoi Easy Round 2023 TEST_107
这个查询的信息就很扫描线啊。不管那么多先离线询问然后按右端点排序,看怎么搞。
我们考虑一个极长子区间可能是长啥样的,有三种可能:
\(1.\) \([l′,r′]=[l,i]\),满足 \(a_{i+1}=x,\forall j\in[l,i],a_j\neq x\)
\(2.\) \([l′,r′]=[i,r]\),满足 \(a_{i-1}=x,\forall j\in[i,r],a_j\neq x\)
\(3.\) \(l′>l,r′<r\),满足 \(a_{l′-1}=a_{r′+1}=x,\forall j\in[l′,r′],a_j\neq x\)
先考虑 \(1\),我们记录 \(las_i\) 表示上一个 \(a_i\) 所在的位置。扫描线每扫过一个 \(i\) 就把线段树上 \(las_i\) 的位置改为 \(i\),这样你在 \(r_j=i\) 时线段树上 \([0,l_j-1]\) 的最大值就代表 \([l_j,r_j]\) 中那个符合 \(1\) 情况的 \(i\)。\(2\) 情况只需要将整个序列倒过来,更新 \(las_i\),同时把询问也倒过来,进行和 \(1\) 情况相同的操作就行。\(3\) 情况扫到 \(i\) 的更新就变成了把 \(las_i\) 位上变成 \((i-1)-(las_i+1)+1\),查询就直接查 \([l_j,r_j]\) 的最大值即可。
再说一下扫描线具体是怎么扫的:我们从 \(1\) 到 \(n\) 遍历原序列,每扫到一个 \(i\) 就 update,将线段树上 \(las_i\) 位置(一般化地来说就是和 \(i\) 形成有贡献的区间的一个位置)修改为 \(i\),表示在查询的区间包含 \(las_i\) 时 \([las_i,i]\) 这段区间是被包含的,可以产生贡献的。每扫到一个 \(r_j=i\) 时就进行查询,把答案更新到数组对应编号中,一次这样的扫描线是 \(O(n\log n+m\log n)\) 的。
for(int i=1,j=1;i<=n;++i){
update(1,0,n,las[i],i); //注意这里会有-1,会涉及到0
while(j<=m&&q[j].r==i){
ans[q[j].id]=max(ans[q[j].id],query(1,0,n,0,q[j].l-1)-q[j].l);
++j;
}
}
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll int
#define ls now<<1
#define rs now<<1|1
const ll N=2000005,M=1919810;
ll n,m,a[N],b[N],ans[N];
ll las[N],bu[N];
struct que{
ll l,r,id;
}q[N];
bool cmp(que x,que y){
return x.r<y.r;
//你扫描线处理询问肯定是扫到右端点处理啊所以排序也是按右端点
}
ll mx[4*N];
void pushup(ll now){
mx[now]=max(mx[ls],mx[rs]);
}
void update(ll now,ll l,ll r,ll x,ll k){
if(l==r){
mx[now]=max(mx[now],k);
return;
}
ll mid=(l+r)>>1;
if(x<=mid) update(ls,l,mid,x,k);
else update(rs,mid+1,r,x,k);
pushup(now);
}
ll query(ll now,ll l,ll r,ll x,ll y){
if(l>=x&&r<=y) return mx[now];
ll mid=(l+r)>>1,ans=0;
if(x<=mid) ans=max(ans,query(ls,l,mid,x,y));
if(y>mid) ans=max(ans,query(rs,mid+1,r,x,y));
return ans;
}
void calc1(){
for(int i=1,j=1;i<=n;++i){
update(1,0,n,las[i],i);
while(j<=m&&q[j].r==i){
ans[q[j].id]=max(ans[q[j].id],query(1,0,n,0,q[j].l-1)-q[j].l);
++j;
}
}
}
void calc2(){
memset(mx,0,sizeof(mx));
memset(bu,0,sizeof(bu));
memset(las,0,sizeof(las));
for(int i=1;i<=n;++i){
b[i]=a[n-i+1];
las[i]=bu[b[i]],bu[b[i]]=i;
}
for(int i=1;i<=m;++i)
q[i].l=n-q[i].l+1,q[i].r=n-q[i].r+1,swap(q[i].l,q[i].r);
sort(q+1,q+m+1,cmp);
for(int i=1,j=1;i<=n;++i){
update(1,0,n,las[i],i);
while(j<=m&&q[j].r==i){
ans[q[j].id]=max(ans[q[j].id],query(1,0,n,0,q[j].l-1)-q[j].l);
++j;
}
}
}
void calc3(){
memset(mx,0,sizeof(mx));
for(int i=1,j=1;i<=n;++i){
update(1,0,n,las[i],i-las[i]-1);
while(j<=m&&q[j].r==i){
ans[q[j].id]=max(ans[q[j].id],query(1,0,n,q[j].l,q[j].r));
++j;
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;++i){
cin>>a[i];
las[i]=bu[a[i]],bu[a[i]]=i;
}
for(int i=1;i<=m;++i) cin>>q[i].l>>q[i].r,q[i].id=i;
sort(q+1,q+m+1,cmp);
calc1();
calc3();
calc2();
for(int i=1;i<=m;++i) cout<<ans[i]<<'\n';
return 0;
}/*你咋滴个说都得理解啊*/
GSS2 - Can you answer these queries II
有参考价值的。显然不能像GSS1那样直接线段树维护前后缀最大子段和了,因为涉及到子区间,考虑能不能离线下来扫描线处理。这里有个trick:我们让线段树的每个叶节点表示以 \(i\) 为开头的最大子段和,每次在线段树上对 \([las_i+1,i]\) 加上 \(a_i\),这样就能保证相同的数的贡献覆盖区间无交,并维护区间历史最大值。维护历史最大值是很容易感性理解的,你还需要同时维护历史最大的 tag。
直接这样就做完了,但我一开始有个地方想不通:像 1 2 3 -10 9,显然选 \(9\) 是最优的,但是我们直接对区间 update 会不会导致前面的贡献为负时影响到后面的值。但并不会,因为只是线段树上 \(9\) 前面的节点会继承负贡献,但从 \(9\) 开始的节点并不会继承负贡献,所以查询的最大值是完全没错的。
P9990 Ynoi Easy Round 2023 TEST_90
因为涉及到子区间个数计数,也就是需要考虑到所有子区间。一个trick是考虑扫描线记录线段树上的历史版本和,很好感性理解,因为我们扫描线是在不断加上新的元素的贡献,相当于将区间右端点的取值范围扩展到了当前的 \(i\),所以所有区间的答案之和就是所有历史版本之和。
然后考虑对每个数考虑他的贡献。显然他能影响到的区间和前几道题一样还是 \([las_i+1,i]\),而他的贡献相当于是将所有区间答案的奇偶性取反。想要统计答案还需要记录每个节点上答案为 \(0/1\) 的区间个数被统计的次数,记为 \(t0,t1\),这样每个区间的答案就是两个 tag 乘上对应答案的子区间个数。注意你每次修改都要对 \([1,n]\) 额外修改一次 t[1].t1++,t[1].ans+=t[1].sum1;,这样这个 \(t1\) 就可以下传到整颗线段树。
没被卡常很开心。
P5290 [十二省联考 2019] 春节十二响
链的部分是部分正解。容易发现 \(1\) 最多有两个支链,所以我们暴力找出这两条链的所有权值,然后 sort 一下,将两条支链上权值排名相同的数相并起来,这样最终答案就只会加上每次合并的两个数中的较大值。
正解?考虑对每个点开一个堆,每次合并 \(u\) 和他的儿子 \(v\),为保证复杂度把 \(\text{siz}\) 较小的堆合并到较大的上,感觉就是启发式合并,复杂度应该是 \(\text{polylog}\) 的,不会太高。
P6626 [省选联考 2020 B 卷] 消息传递
多次询问与 \(u\) 距离为 \(k\) 的点的个数。
考虑点分治,把每个询问离线下来挂到点上。令当前的分治中心为 \(u\),我们记录下 \(u\) 子树中每种深度的点有多少个,对于 \(u\) 上的询问来说贡献就是 \(cnt[k-dept[u]]\)。当我们进入儿子 \(v\) 时,\(v\) 子树中的点的深度相对于 \(u\) 子树中的要小一,所以进入之前要先更新 \(cnt\),出来之后也是。具体来说更新方法就是遍历一遍子树:
void dfs_upd(ll u,ll fa,ll k){
cnt[dept[u]]+=k; //k=1或-1
for(int v:g[u]){
if(v==fa||vis[v]) continue;
dfs_upd(v,u,k);
}
}
然后按正常点分治框架来就行了,注意多测清空。
P8600 [蓝桥杯 2013 省 B] 连号区间数
自己想的做法假了,没模拟样例,直接被叉了(
一个关键的转化是:已知合法的充要条件为 \(\max-\min=r-l\) ,转化后有等式 \(\max\limits_{l\le i\le r}a_i-\min\limits_{l\le i\le r} a_i+l=r\) 并不难发现有不等式:\(\max\limits_{l\le i\le r}a_i-\min\limits_{l\le i\le r} a_i+l\ge r\) 成立,所以只需要找到左边式子的最小值个数即是答案。
P4656 [CEOI2017] Palindromic Partitions
显然用到哈希。我们发现,从串的两端开始,如果出现相同的子串,那么直接把他们各划分成一段对最终答案是一定不劣而且合法的。但是你可能会想假如中间有个串 \(A\) 必须和已选择过的串 \(B\) 结合才能构成回文,那上述方法可能就假了,但你模拟不出这种情况,像是 \(ABBA\) 和 \(ABA\) 的情况按上述方法均是正确的,所以就对了。
P5070 [Ynoi2015] 即便看不到未来
CF522D
扫描线板题,独立秒了欸。直接扫描线,将 \(las[i]\) 修改成 \(i-las[i]\) 然后查区间最小值就做完了。
P1648 看守
先考虑二维的情况怎么搞,这里需要从曼哈顿距离的式子入手。
我们将绝对值拆开,即 \(|a_i-b_i|=\max(a_i-b_i,b_i-a_i)\)
同时注意到 \(\max\) 具有分配律,即 \(\max(a,b)+\max(c,d)=\max(a+c,a+d,b+c,b+d)\)
所以可以将原式化为 \(\sum\limits_{i=1}^d |a_i-b_i|=\max\limits_{q_i\in\{-1,1\}}(\sum\limits_{i=1}^d q_i\times a_i+\sum\limits_{i=1}^d -q_i\times b_i)\),\(q_i\) 即枚举 \(a_i,b_i\) 的符号。
考虑多引入一个 \(C\) 点再来求最大距离,得:\(ans=\max(\sum\limits_{i=1}^d q_i\times a_i-\sum\limits_{i=1}^d q_i\times b_i,\sum\limits_{i=1}^d q_i\times a_i-\sum\limits_{i=1}^d q_i\times c_i,\sum\limits_{i=1}^d q_i\times b_i-\sum\limits_{i=1}^d q_i\times c_i,\cdots)\)
再加上将符号位取反的式子取 \(\max\) 就是最后答案,这样你会发现,答案实质上就是 \(\sum\limits_{i=1}^d q_i\times x_i\) 的最大值减最小值。那么只要枚举了各个符号位的取值,答案就可以在 \(O(n)\) 的复杂度内求出,那么总复杂度就是 \(O(2^dn)\)。
P9743 「KDOI-06-J」旅行
比较经典的 dp 思路模式,应该记住。
考虑将所有需要考虑的条件都扔进状态标识里,这样会整一个五维的 \(dp[x][y][k][ka][kb]\) 表示在 \((x,y)\) 花了 \(k\) 块钱且剩 \(a\) 张横票和 \(b\) 张竖票的方案数。转移中考虑枚举在 \((x,y)\) 买多少张票,转移方程比较好想,令 \(c=k-a_{i,j}\times ca-b_{i,j}\times cb\),转移式为:
这样是 \(O(n^7)\) 的,最好可以得 65pts。考虑怎么优化掉枚举,观察到 \(O(n^2)\) 转移实际上是在后两维上求一个矩形中的元素之和,那么可以考虑用二位前缀和的方式来 \(O(1)\) 完成转移。主要二位前缀和取不到 \(ca=0,cb=0\),所以要多加上 \(dp_{x-1,y,k,ka+1,kb}+dp_{x,y-1,k,ka,kb+1}\)。再来发现数组开不下,于是可以滚动数组优化掉 \(x\) 或 \(y\) 这一维,复杂度 \(O(n^5)\),能过了。(一个优化:如果现在买的票已经不可能贡献了,就不再转移了)
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=50,M=1919810,mod=998244353;
ll n,m,K,a[N][N],b[N][N],ans[N][N];
ll dp[2][N][91][N][N];
//在 (x,y) 已经花了 k 块钱,剩 a 张横票和 b 张竖票的方案数
int main(){
//ios::sync_with_stdio(0);
//cin.tie(0); cout.tie(0);
cin>>n>>m>>K;
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
cin>>a[i][j];
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
cin>>b[i][j];
dp[1][1][0][0][0]=1;
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j){
if(i>1) dp[i&1][j][0][0][0]=0;
for(int k=1;k<=K;++k)
for(int ka=0;ka+i<=n;++ka)
for(int kb=0;kb+j<=m;++kb){
ll x=0;
//cout<<i<<" "<<j<<" "<<k<<" "<<ka<<" "<<kb<<'\n';
if(i>1) x+=dp[(i-1)&1][j][k][ka+1][kb];
if(j>1) x+=dp[i&1][j-1][k][ka][kb+1];
if(ka&&k>=a[i][j]) x+=dp[i&1][j][k-a[i][j]][ka-1][kb];
if(kb&&k>=b[i][j]) x+=dp[i&1][j][k-b[i][j]][ka][kb-1];
if(ka&&kb&&k-a[i][j]-b[i][j]>=0) x-=dp[i&1][j][k-a[i][j]-b[i][j]][ka-1][kb-1];
x=(x%mod+mod)%mod;
dp[i&1][j][k][ka][kb]=x;
if(k==K&&ka==0&&kb==0) ans[i][j]=x;
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j)
cout<<ans[i][j]<<" ";
cout<<'\n';
}
return 0;
}/*滚动数组他妈不要用异或
注意要用一个ans数组记录答案,因为有滚动数组
我是真的不会啊啊啊阿哭*/
的移动次数。模拟一下排序过程,可以发现每一个轮次(也就是外层循环)中每一个数至多被前移一次,还有某个数会一直往后移直到遇到比它更大的数。那么可以想到,每个数向前移动的次数就是他前面比他大的数的个数,记为 \(cnt_i\),\(\sum cnt_i\) 就是总的移动次数。
然后能想到的是二分移动的轮数,得到的轮数记为 \(x\)。若某个 \(cnt_i\le x\) 说明 \(a_i\) 是已经不会再移动的,我们考虑把这些 \(a_i\) 单独挑出来排序,然后再按顺序塞回原来的数组的空中。当然若 \(cnt_i>x\) 则 \(a_i\) 在 \(i-x\) 位处。最后再暴力跑一遍排序把 \(k\) 用完,如果还剩就输出无解。(吐糟只有第一个点是无解,而且我直接复制样例中的无解,然后多个空格少了十分/ll)
P1896 [SCOI2005] 互不侵犯
要想到两个点:状态设 \(dp[i][j][k]\) 表示第 \(i\) 行状态为 \(k\),前 \(i\) 行共放了 \(j\) 个国王时的方案数;然后是直接枚举合法状态来转移。
QOJ8831 Chemistry Class
becoder Day2 T2,某个人贪心假完了,本来可以AC的,结果啥都不会,寄了(
结论题。首先判掉无解很简单,从小到大排序看直接匹配相邻两个数是否都 \(\le A\),这样一定能使最大的匹配值最小,交换一定不优。然后发现匹配的形式有两个结论:
-
匹配之间的连线不会出现交叉,因为有交叉时交换匹配后必然更优。
-
不会出现多于两层的嵌套,证明可以发现多于两层一定有方案拆成两层以内的嵌套。
有了以上结论,可以知道配对的形式一定是一些段,比如在 \([l,r]\) 中,\(l,r\) 配成一对,中间的就两两相邻的匹配。考虑 dp,设 \(dp[i]\) 表示前 \(i\) 个数(注意枚举的 \(i\) 都是偶数)的最大答案。预处理相邻两个合法匹配数的前缀和,朴素转移 \(O(n^2)\),可以用线段树/单调队列优化,但这个题有点卡常。
一个错误的贪心是直接把相邻的差值小于 \(B\) 的数匹配在一起,然后从序列中移除(可采用链表的方式),同时保证剩下的匹配都 \(\le A\),可以这样实现:
ll nm=2*n,ans=0,fl=0; //是否有多的未匹配点
for(int i=1;i<=nm;++i){
if(vis[i]) continue;
if(abs(a[r[i]]-a[i])<=B){
if(fl&&abs(a[r[r[i]]]-a[l[i]])>A){
fl^=1;
continue;
}
vis[i]=vis[r[i]]=1;
del(i),del(r[i]);
++ans;
}
else fl^=1;
}
P11081 [ROI 2019 Day 1] 自动驾驶
没想到转化,没发现性质,死了。
转化是把每个点的积雪厚度是否不超过 \(k\) 转化成这个点被清空的时间是否大于等于当前询问时间 \(t-k\)。
性质是路线至多拐两个弯,感性理解原因显然,因为多转一个弯一定更劣。然后你就可以分讨是能直接走曼哈顿距离还是要多绕一点才能到达。考虑用两个线段树维护行/列打的时间戳的最大最小值以及其位置。
P6370 [COCI2006-2007#6] KAMEN
绿色模拟题,考虑用 set 维护每一列 X 或是 O 的位置,然后模拟下落过程,每次用lower_bound找下一个位置。但是这样会被反复横跳卡成 \(O(nr\log r)\)。
列数很小。发现对于同一列的下落路径,每次改变的都是一段后缀,所以可以对第 \(i\) 列维护从这一列开始扔球,到第 \(j\) 行时在哪一列。要注意的是我们会直接定位到一个有 X/O 的位置,但是实际上球应该在它上面一格。
P3052 [USACO12MAR] Cows in a Skyscraper G
奔着状压dp来做,结果一眼还看不出来哪里能状压,更像是折半搜索(
无法直接对物品的分组状态进行状压,但可以对每一组所含的物品状态进行状压。具体来说,设 \(dp[i][j]\) 分了 \(i\) 组,物品被放入情况为 \(j\),表示最后一组的重量,因为状态中前面每组都放满了,所以只用考虑最后一组。然后转移就枚举还有哪个物品不在状态 \(j\) 中,然后合并一下,填表法更新就行了。
距NOIP2024还有50天
P4568 [JLOI2011] 飞行路线
分层图最短路板子。直接按分层图的建法建图之后跑 dij 就完了。
分层图一般用于一些会改变边权的问题,过程:分成 \(k+1\) 层图,每层图和原图一样。其中第 \(i\) 层图是用了 \(i\) 次优惠到达的图。对于第 \(i\) 层中任意一条 \(u\) 连向 \(v\) 的边,要同时连一条 \(u\) 指向第 \(i+1\) 层的 \(v\) 的边,权值为改变后的权值。然后跑最短路即可,终点在第几层就表示改变了几次权值。
P9751 [CSP-J 2023] 旅游巴士
有两个限制条件:一是路径的长度要是 \(k\) 的倍数,二是边的开放时间。
先考虑 \(k\) 的倍数限制。发现 \(O(nk)\) 是能写的,于是考虑分层图,第 \(i\) 层的点表示到达这个点的距离模 \(k\) 为 \(i\),建边也就是当前层的 \(u\) 连向下一层的 \(v\),然后跑最短路找到模 \(k\) 为 \(0\) 的层中 \(1\to n\) 的最短路,也就是第零层到第 \(k\) 层。
对于开放时间的限制,题解中说分层图跑dij的过程中可以直接等,但我不到啥意思啊。跑dij的过程中如果遇到一个点的开放时间仍大于当前的距离,那么就直接加上少的距离就行了?
P11188 「KDOI-10」商店砍价
记得在 set 中用 lower_bound/upper_bound 要这样写成 s.lower_bound(x) 就行了,要不然复杂度是假的。
P4571 [JSOI2009] 瓶子和燃料
简单题,感觉会被降绿。显然两个容量为 \(a,b\) 瓶子能留下来的油量是 \(\gcd(a,b)\),然后发现这就是裴蜀定理:线性方程 \(a_1\cdot x_1+a_2\cdot x_2+\cdots+a_n\cdot x_n\) 能凑出的最小正整数是 \(\gcd(a_1,\cdots,a_n)\)。题目就转化成找出 \(k\) 个瓶子使得 \(\gcd\) 最大。显然不能枚举瓶子的组合,于是考虑枚举哪些 \(\gcd\) 在各个数的因数中出现次数 \(\ge k\)。这个题的数据完全允许 \(O(n\sqrt{V})\) 枚举出所有因数,然后就做完了,可以用 map 来存因数出现次数。
P3792 由乃与大母神原型和偶像崇拜
做法是判断 maxn-minn==r-l 和 minn 到 maxn 的平方和是否等于这段区间的平方和。等差数列是不对的,因为能出现 \(1+1=2\) 的情况,但我们能发现 \(1^2+1^2\ne 2^2,1^2+2^2\ne 3^2\),平方运算是不满足结合律的,所以考虑用线段树维护区间最小最大值和平方和,这个题要用 __int128。\(1\sim n\) 的平方和为 \(\dfrac{n(n+1)(2n+1)}{6}\)
P3435 [POI2006] OKR-Periods of Words
考虑要使周期最长,就要使原串中周期以外的子串最短。
令串 \(S\) 长 \(n\),其一个周期为 \(S_{1\sim i}\),根据题目中对周期的定义,容易发现的是 \(S_{i+1\sim n}\) 一定是 \(S_{1\sim i}\) 的前缀。由于 \(S_{1\sim i}\) 是 \(S\) 的前缀,\(S_{i+1\sim n}\) 是 \(S\) 的后缀,那么可以得出结论:\(S_{i+1\sim n}\) 是 \(S\) 的 \(\text{border}\)。
为了使 \(S_{1\sim i}\) 最长,要让 \(S_{i+1\sim n}\) 最短。那么题目也就转换成求 \(S\) 的每个前缀的最短 \(\text{border}\),每个前缀的答案就是其长度减最短 \(\text{border}\) 的长度,用KMP来求也就是 \(len-nex[i]\)。
朴素求每个前缀的最短 \(\text{border}\) 可以不断跳当前串的 \(\text{border}\),依据是 \(\text{border}\) 的性质。这样会超时,但是这个跳 \(\text{border}\) 的过程完全可以像并查集那样路径压缩。就做完了。
P2375 [NOI2014] 动物园
题意就是对于每个前缀找到小于等于其长度一半的 \(\text{border}\) 个数。还是想到不断跳 \(\text{border}\) 直到长度小于等于当前前缀的一半,令跳到的这个 \(\text{border}\) 为 \(s\)。注意到 \(s\) 的 \(\text{border}\) 数就是这个前缀的合法 \(\text{border}\) 数,这个可以一遍 KMP 的时候求出。
肯定还是不能直接暴力跳的,但这个题就不能像上个题那样路径压缩来做了。考虑怎么减少重复的跳转,既然从前缀的 \(\text{border}\) 开始往前跳不好搞,那不如让已经得到的 \(\text{border}\) 往后扩展。我们发现每次求完答案跳到的 \(\text{border}\) 的长度一定对于下一个前缀也合法,但他就不一定是 \(\text{border}\) 了,那不如直接再按照KMP的方法求得新的 \(\text{border}\),这样子均摊下来跳的次数就也是 \(O(n)\) 的了。
Drink Bar
模拟赛的题。70pts可以通过比较好想的 \(O(n^2\log n)\) 做出,虽然我人菜常数大得一批。正解的话难点在于不要想数点而通过这个对三元组计数的本质想到容斥。
容易发现每个子集都可以等价成一个 \(|S|\le3\) 的子集,因为是三元组,最多只会有三个元素让其改变。形式话来说就是 \(\nexists(A,B,C)\) 使的 \(\forall S\in U\) 满足 \(|S|>3\)。
考虑分三种情况讨论:
第一种,\(|S|=1\),也就是有一个元素的 \(A,B,C\) 都是最大的。显然对答案贡献为 \(n\)。
第二种,\(|S|=2\)。总方案数为 \(\binom{n}{2}\),考虑容斥。这种情况下不合法方案显然是存在一个元素的 \(A,B,C\) 都是最大值,那么枚举一下这个元素,方案数就是:
发现这是个三位偏序问题,考虑CDQ分治解决。
第三种,\(|S|=3\)。总方案数为 \(\binom{n}{3}\),仍然考虑容斥。不合法方案是某个元素有多于一个最大值,于是分别考虑某个元素的 \(AB,AC,BC\) 最大。确定了最大元素后就是个二维偏序了,可以树状数组做,但是注意如果确定的这个元素在第二种情况中被当作 \(A,B,C\) 同时最大的值时还要把它对答案的贡献给加上,避免算重。
P3065 [USACO12DEC] First! G
容易想到建trie,考虑一个串不合法的情况。首先是如果它的前缀出现过就不合法,这个显然。然后考虑字母顺序的影响,令当前所在节点为 \(rt\),要走的儿子对应字母为 \(i\),其它儿子的字母统称为 \(j\),可以观察到在后续路径中如果要走 \(j\) 的时候同时出现了 \(i\),那么就是不合法的,可以直接用数组记录。
但有个坑:若 \(a>b,b>c\) 则 \(a>c\),这是具有传递性的,直接用数组记录只能记一层,所以要将这些关系建成图来跑,发现如果图上出现环则无解,用拓扑排序来做是简单的。注意清空。
[ABC134F] Permutation Oddness
我怎么没有补这个题啊,芝士一个基本要学了trick才会的题。
将题意转化为球 \(p_i\) 和盒子 \(i\) 的匹配问题,将球放在左边,盒子放在右边,在每个球之间画一条水平的线,每对匹配的球和盒子间再连一条线,这个排列的价值就是球盒之间连线与水平线的交点个数。
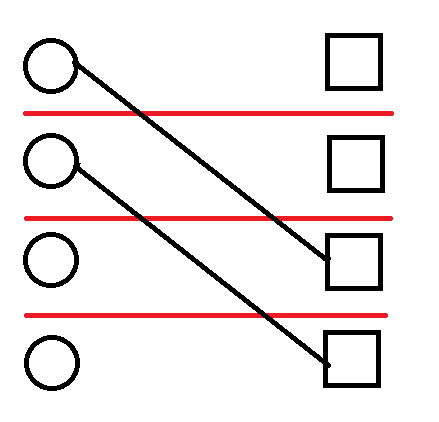
考虑将球盒匹配的过程看作是 \(n\) 阶段的决策,即第 \(i\) 阶段(也就是常说的“前 \(i\) 个”)考虑让编号为 \(i\) 的球和盒子怎么匹配。
于是设状态 \(dp[i][j][k]\) 表示考虑前 \(i\) 个球盒(球盒不分开),有 \(j\) 个球盒没有匹配,当前已经匹配的球盒的价值,答案即 \(dp[n][0][K]\)。
考虑转移,先给出转移式再理解:
第一行表示匹配了一组(只匹配 \(i\) 球/盒或自己匹配自己),有三种情况:
\(1.\) \(i\) 号球和 \(j\) 个没配对的盒子匹配,共 \(j\) 种
\(2.\) \(i\) 号盒子和 \(j\) 个没配对的球匹配,共 \(j\) 种
\(3.\) \(i\) 号球和 \(i\) 号盒子匹配,共 \(1\) 种。
根据加法原理,共 \(2\times j+1\) 种方案,从 \(dp[i-1][j][k-2\times j]\) 转移来。
第二行表示匹配了两组,所以 \(i\) 号球盒就不能相匹配了,两种情况:
\(1.\) \(i\) 号球与没配对的 \(j+1\) 个盒子匹配,共 \(j+1\) 种
\(2.\) \(i\) 号盒子与没配对的 \(j+1\) 个球匹配,共 \(j+1\) 种
乘法原理,共 \((j+1)^2\) 种方案,从 \(dp[i-1][j+1][k-2\times j]\) 转移来。
第三行就是没有进行匹配,就只有 \(1\) 种方案,直接转移。
\(k\) 从 \(k-2\times j\) 转移来是因为每次匹配都会使排列价值增加 \(2\times j\)。
于是代码就按着这个写就行了,注意每一层循环的 \(k\) 从 \(2\times j\) 开始枚举。
P4302 [SCOI2003] 字符串折叠
简单题。容易看出来在合并区间,且注意到 \(n\le 100\),考虑区间dp。考虑一个区间可以枚举一个断点 \(k\) 合并,也可以把它折叠起来,需要判断是否为循环节,显然用哈希来做。要注意的是折叠过后的数字长度可能是 \(1/2/3\) 位数,判断一下,就做完了。
P3698 [CQOI2017] 小Q的棋盘
贪心地想,如果走的步数 \(k\) 小于最深节点深度 \(maxd\) 那么显然走的节点数最多是 \(k+1\)(要算上根)。考虑多出来的步数,发现每多两步就可以先走到一个新节点再返回到最深链上,感性理解一下是很对的,就不用dp做完了。dp的话因为数据较小所以可以设 \(dp[u][j][0/1]\) 表示在 \(u\) 的子树中走 \(j\) 步时能否回到 \(u\) 的答案。
CF1613D MEX Sequences
显然想到dp。注意到合法的 \(\text{mex}\) 序列有两种形态:一是去重后不下降且邻项的差不超过 \(1\),形如 \(0,0,1,1,2,2,2\) 这种;二是前一半为第一种序列,令到前一半最后一位的 \(\text{mex}\) 为 \(x\),则后一半只可能由 \(x+1,x-1\) 组成,形如 \(0,1,2,4,2,2,4\) 这种。
可以根据结尾的 \(\text{mex}\) 来计数,考虑设状态 \(dp[x][0/1]\) 表示到子序列最后一位的 \(\text{mex}\) 为 \(x\) 时第一种/第二种序列的个数。转移是好转移的,令当前枚举到 \(x=a_i\)(注意我们在序列中枚举到的是 \(x\),但是此时的 \(\text{mex}\) 只可能是 \(x+1/x-1\)),则转移为:
注意判断第三行的 \(x\) 是否不为 \(0\),最后的答案就是 \(\sum\limits_{x}dp[x][0]+dp[x][1]\)。没做出来的原因应该是把问题给复杂化了,菜死,CF*1900也没做出来,枯了。
P8860 动态图连通性
容易发现对于每条边如果第一次无法删除的话那么后续也无法删除,如果第一次就删掉了那么后续就直接输出 \(0\)。可以假设每条边都会被删一次,我们考虑令 \(d_i\) 为每条边被删的时间,如果不会被删则 \(d_i=q+1\)。一个想法是找到所有删除操作结束后的唯一一条路径是哪条,显然这条路径上的所有边都不会被删。
考虑这条路径满足什么性质。首先能看出 \(d_i\) 最小的边要尽量大,这样最后在某一时刻剩下的边一定是这一条路径上的。同时发现次小的 \(d_i\) 也要最大,于是可以推广出实际上是 \(d_i\) 从小到大排列后要求字典序最大。这里就有一个用 Dijkstra 求字典序最小/大的一个trick:每次松弛时只需要比较最后走的这条边的 \(d_i\),选取 \(d_i\) 最大的一个,若 \(d_i\) 相同则比较走上一步的 \(dis\),证明考虑反证法假设有一条道路比这样求出的更优。
实际上又能发现不需要真的求出 \(dis\),只需要比较两个点在 Dijkstra 过程中谁先被扩展出来,谁的 \(dis\) 就更小,松弛操作都不需要了。这样跑一边 Dijkstra 就能记录下最后剩下的路径,然后上面的边也就不能被删除了。还有其实 Dij 的队列里塞的是边。代码好写,难想。
怎么想到这个做法的呢?首先直接在线搞动态图连通性基本不可做,考虑离线是自然的。并且你要尝试对问题进行一些转化,这个题就是转化成找到最后的路径。
P2466 [SDOI2008] Sue 的小球
每次收集彩蛋是不花时间的,所以对于一段彩蛋区间 \(x\in[l,r]\),一定不会出现 \(l\to r\to x\) 的选择顺序,这样一定不优。这就代表如果我们区间dp的话就不需要在中间枚举断点了。也就是复杂度只有 \(O(n^2)\),放在这个题中就能过了。
同时明显选完一段彩蛋后这个人一定是停留在左端点或右端点,那么我们就可以考虑设状态 \(dp[l][r][0/1]\) 表示最后停留在 \(l\) 或 \(r\) 时 \([l,r]\) 的最大分数。但是有个问题,就是收集过程是有时间的,但我们不可能把时间这维加入状态中。有个trick:拿一段彩蛋的时间是固定的,拿这段区间时所有彩蛋下降的高度,也就是对总答案的负贡献也是固定的,所以我们可以将dp的状态值得意义改为 \([l,r]\) 的最大贡献,这个贡献的含义就是 这段区间的分数 \(-\) 当前未被收集的彩蛋的下降高度和。这样就相当于把会因为时间变化造成的负贡献提前算进答案里面了。考虑提前将这些负贡献加到初始状态中,具体来说就是让 dp[i][i][0/1]=a[i].y-abs(x0-a[i].x)*sum[n];
转移的时候讨论一下从 \([l,r-1]\) 和 \([l+1,r]\) 的较大值就行了。注意我们肯定先对彩蛋按 \(x\) 排序,并且除以 \(1000\) 放最后来算。
P1220 关路灯
和上一道一模一样,也是考虑将时间变化导致的负贡献提前加入状态中。这一类区间dp能 \(O(n^2)\) 做的原因就是选定一段区间后的最优策略一定是直接从一端走向另一端,所以不用枚举断点。
P4870 [BalticOI 2009 Day1] 甲虫
还是类似前两道,但注意不用喝完每一滴水,所以当其价值为负时就不要喝了。所以我们考虑枚举喝的水滴的数量,这样是能得到最优答案的。
为什么呢?这道题一个很关键的性质是每个水滴的初始价值是相同的,也就保证了dp数组记录喝完 \([l,r]\) 的最优答案的正确性。因为不会出现喝 \(x\) 位置水已经为负贡献但喝 \(x-1\) 位置的仍然是正贡献。
[ABC219H] Candles
上一道的加强版,物品初始价值不同,价值衰减速度一样,价值为负时不能取。
直接说结论:将状态改为 \(dp[i][j][k][0/1]\),多的一维 \(k\) 表示在这个区间以外还要选 \(k\) 个物品。因此转移时除了要讨论在左/右端点,还要讨论这个端点上的物品是否要被选择。具体来说:
\(dp[i][j][k][1]\) 转移同理。初始化考虑加入一个 \((0,0)\) 作为初始所在点,将序列按 \(x\) 排序, 令初始点下标为 \(p\),让 \(dp[p][p][k][0/1]=0,k\in[0,n]\)。总复杂度 \(O(n^3)\)。其实就是将上一道题的枚举选取物品个数从外层循环转移到了状态表示中。
[AGC034D] Manhattan Max Matching
不管曼哈顿距离,容易看出这是二分图,暴力 \(O(n^2)\) 连边后也显然是跑二分图最大权匹配。考虑费用流来做,要建源点 \(s\) 向所有左部点连容量 \(1\) 边权 \(0\) 的边,所有右部点也这么向汇点 \(t\) 连边。
考虑优化建图。关于曼哈顿距离的最大值,前面有个题已经说了这个trick了:考虑拆绝对值,这样曼哈顿距离的四个坐标取值都有正负号的取值,共16种曼哈顿距离的式子。我们要暴力全部连边的原因是不能简化曼哈顿距离的形式让所有点可以连在固定的几个点上计算。现在可以了,考虑建四个点,让 左部点向这四个点/这四个点向右部点 连一条容量 \(inf\) 权值为 \(\pm x_i\pm y_i\) 的边,然后直接跑最大费用最大流就行,这个题保证了两部点的数量相同且要匹配完。
P5658 [CSP-S2019] 括号树
简单题,自己做出来的。考虑添加一个括号会产生的影响。添加一个左括号对前面的答案没用,塞到栈里。添加一个右括号时能和左括号匹配。如果一个左括号前面是合法子串连续段,那么答案额外 \(+\) (合法字串个数),否则只 \(+1\)。匹配的左右括号间一定是合法字串,这么转移的实际意义是新产生的合法字串可以是 \((A)\) 或 \(B(A)\) 的形式。开数组维护每个右括号是多少个合法字串相连的结尾,记为 \(fl\),和每个结点的答案 \(dp[u]\)。
转移的话就是先直接继承父亲的答案,如果是右括号再看能不能匹配,如果能匹配且左括号前一个是右括号,那么就再加上其 \(fl\) 就行了。
[AGC014D] Black and White Tree
容易发现在一个点有至少两个叶子为儿子时先手必胜。但我们发现这不是唯一一种染出连续白点的方案。考虑先选一个点作为根染白,在某个子树内任选一个点染黑,如果有一个子树的大小为奇数,那么 不断染白叶子父亲再染黑叶子 就可以最后得到连续的三个白点,这是必胜的,但是第一个黑点也能选在这个子树中,所以需要至少两颗子树能完成这样的操作。
也就是说,存在一个点至少有两个子树的点数为奇数先手必胜,如果不存在则代表树存在完美匹配,后手必胜。
[ARC168D] Maximize Update
没见过真做不出来。考虑设 \(dp[l][r]\) 表示只用操作(形容词)区间在 \([l,r]\) 内的操作(名词)能最多能操作(动词)多少次。但是直接转移是做不到的,于是考虑用 \(O(n^3)\) 的时间预处理 \(f[l][r][i]\) 表示能否用 \([l,r]\) 以内的操作对 \(i\) 染色。这样转移时我们枚举最后一个被染黑的格子,将它作为断点,转移就是 \(dp[i][j]=\max(dp[i][j],dp[i][k-1]+f[i][j][k]+dp[k+1][j])\),不过注意也可以直接合并两端区间的答案即 \(dp[i][j]=\max(dp[i][k],dp[i][k+1])\)。
P5662 [CSP-J2019] 纪念品
看起来是完全背包。先考虑 \(N=1\),设 \(dp[i][j]\) 表示第 \(i\) 天有 \(j\) 块钱时在 \(i+1\) 天能赚的最多钱数。转移就是完全背包,代价是今天的价格,收益是明天的价格。但为什么可以只看第二天的收益呢?首先如果直接看后缀最大值的话可能会出现第三天最高价但是第二天就没钱的情况。只看第二天的话你考虑可能会出现一个物品第三天卖比第二天卖更优,但实际上完全背包是能把这种情况包含的。而且代码写出来也是对的。扩展到多物品就只是加了一维循环,每天的背包做完后再更新一下 \(m\),最后的答案就是 \(m\)。
P11232 [CSP-S 2024] 超速检测 T2
简单题,但是 \(m\) 写成 \(n\) 了。考虑把 \(a\ge 0\) 和 \(a<0\) 的车分开讨论。先解决第一问,对于 \(a\ge 0\) 的车取最后一个监测点判断瞬时速度就行,对于 \(a<0\) 的 lower_bound 找到第一个能检测到它的监测点,一样的判断即可。
对于第二问,\(a\ge 0\) 的部分显然直接选最后一个监测点是最优的。\(a<0\) 的话考虑对每个车找到离它最远的能检测到他超速的监测点,将车的起点到这个最远的监测点作为一段区间,问题转化成如何用最少的关键点覆盖所有区间。
每个右端点都是能选的,所以考虑按右端点从小到大排序,然后不断向后扩展直到当右端点无法支配区间。这样选一定是最优的,可以使选择个数最少,还能使最后一个选择的点尽量远。
考虑最远的这个点是否也能支配所有 \(a\ge 0\) 的车车,可以对所有 \(a\ge 0\) 的车求出离他最近的能测出他超速的监测点,如果这些监测点中最远的没有 \(a<0\) 中的最远点远,那么就不用额外加上这一个点,否则要加。最后注意第二问中我们求出的是最少开启多少个,要求给出最多关多少个,所以答案是 \(m-ans2\),不是 \(n-ans2\) !!
P11233 [CSP-S 2024] 染色 T3
令 \(dp[i][j]\) 表示当前dp到第 \(i\) 位,上一个和 \(i\) 不同色的位置是 \(j\) 时的最大价值。考虑刷表法,每个\(dp[i][j]\) 能转移到 \(dp[i+1][j]\) 和 \(dp[i+1][i]\)。考虑化简状态,将 \(dp[i]\) 定义为 \(dp[i][i+1]\),则易得出转移式 \(dp[i]=\max\limits_{j=1}^{i-1}(dp[j]+[a[j-1]=a[i]]\times a[i]+\sum\limits_{k=j}^{i-2} [a[k]=a[k+1]]\times a[k])\),到现在还是 \(O(n^2)\) 的。
然后你发现后面那两项都是可以直接用数据结构维护的,所以 \(O(n\log n)\) 就有了,只要实现不烂应该是能过的,\(O(n)\) 的还不太会。
MZOJ #1021 简单题
数据较小,点之间存在支配关系,考虑费用流。建图方式:将每个点拆成左部点和右部点,\(S\) 向每个左部点连一条 \(w=1,c=0\) 的边,右部点向 \(T\) 连一条 \(w=1,c=0\) 的边。\(S\) 向右部点连一条 \(w=1,c=a[i]\times d[i]\) 的边,表示直接付出这个点的代价。每个左部点向每个能支配的右部点连一条 \(w=1,c=0\) 的边,这样因为流量必须为 \(n\) 所以能保证每一个点在支配另一个点后不能再支配其他点。最小费用最大流即可。
P3410 拍照
你需要知道什么是最大权闭合子图,即给定一张有向图,每个点都有一个权值(可以为正或负或 \(0\)),你需要选择一个权值和最大的子图,使得子图中每个点的后继都在子图中。
做法:考虑网络流,若 \(u\) 节点权值非负,\(s\) 向 \(u\) 连一条流量为 \(val[u]\) 的边,权值为负则 \(u\) 向 \(t\) 连一条流量为 \(|val[u]|\) 的边。原图上的边流量为 \(\inf\),所有正权值减去最小割即是答案,这是板子题,证明懒得证。
[AGC061C] First Come First Serve
第一想法是相交的区间会对答案造成额外贡献,这样可以交换这两个人的选择顺序让答案 \(\times 2\),但显然这样会产生很多不存在的贡献。考虑容斥,对于每个区间,把在他前面且和他没有交集的区间的答案给减去。考虑 dp,记录 \(dp[i]\) 表示dp到当前区间的答案,找到无交的区间可以考虑双指针,然后减去这些区间的答案。这样转移就是简单的 \(dp[i]=2\times dp[i-1],dp[i]-=dp[j]\)。
一个markdown里写太多了渲染不过来了(
MZOJ #1053. 画家
不要想直接求区间不同颜色个数,这样搞复杂了,转化成求出现次数为奇数次的颜色个数。求出这个个数后和区间长度比较一下就行了。为什么要求这个呢?因为这样就可以用bitset维护。考虑分块,每个块内维护一个bitset,同时将bitset按前缀和的方式来维护,这样子修改时是 \(O(\sqrt{n})\) 的,查询也是 \(O(\sqrt{n})\)。
考虑扩展到树上,注意到我们可以在欧拉序上用一段区间中仅出现一次的表示树上的一条链,而两次的本来就会被 XOR 掉,所以跑一个欧拉序之后就变成了序列问题。代码不难写。
下面是几道单调队列优化dp。
P3572 [POI2014] PTA-Little Bird
这个题比较毒,只能单调队列优化dp不能线段树维护。朴素转移很简单:\(dp[i]=\max\limits_{j=i-k}^{i-1}dp[j]+[a_i\ge a_j]\)。复杂度要求 \(O(qn)\),考虑单调队列优化。具体怎么操作看代码,给一个单调队列优化的模板,注释采用了经典的选手退役模型:
h=1,t=0;
for(int i=1;i<=n;++i){
while(h<=t&&i-q[h]>k) ++h; //弹出已经毕业的人
if(h<=t) dp[i]=...; //更新最强的人
while(h<=t&&dp[q[t]]....) --t; //被新生单调队列的学长移出队列,退役
q[++t]=i; //新生入队
}
P2569 [SCOI2010] 股票交易
不难的题,还是先写出朴素转移,状态是好设的:令 \(dp[i][j]\) 表示第 \(i\) 天有 \(j\) 支股票的最大收益,刷表法考虑第 \(i\) 天有四种转移的情况:
- 啥都不干,直接从前一天转移来 \(dp[i][j]=dp[i-1][j]\)
- 第一次买股票,收益为 \(dp[i][j]=-j\times AP_i,j\in[0,AS_i]\)
- 枚举在第 \(i-w-1\) 天有 \(k\) 支股票,今天买到 \(j\) 支,\(dp[i][j]=\max\limits_{k=j-AS_i}^{j-1}(dp[i-w-1][k]-(j-k)\times AP_i)\)
- 枚举在第 \(i-w-1\) 天有 \(k\) 支股票,今天卖到 \(j\) 支,\(dp[i][j]=\max\limits_{k=j+1}^{j+BS_i}(dp[i-w-1][k]+(k-j)\times BP_i)\)
复杂度瓶颈在于枚举 \(k\) 的朴素转移,总复杂度 \(O(nP^2)\)。容易发现,在固定了 \(i,j\) 之后,第三种和第四种转移就是在长度固定的连续单调区间中找最值,显然能单调队列优化,能优化到 \(O(nP)\)。注意单调队列初始的指针赋为 \(h=1,t=0\),这样才能让第一个元素正确。
P2034 选择数字
发现以前用优先队列过了一道单调队列优化dp的题,看来是自己做的了。
朴素转移很简单,令 \(dp[i]\) 表示前 \(i\) 个数不选 \(i\) 时的答案:\(dp[i]=\max\limits_{j=i-k}^i(sum[i-1]-sum[j-1]+dp[j-1])\),答案便是 \(dp[n+1]\)。
单调队列是显然的,但我用的优先队列。考虑到转移过来的 \(j\) 的范围只和 \(i\) 有关且是单调的,于是考虑在优先队列里塞 pair(-sum[j-1]+dp[j-1],1),前者是只和 \(j\) 相关的贡献,后者是编号。当枚举到 \(i\) 时取堆顶元素就行了,如果无法从其转移就不断弹出。
P2254 [NOI2005] 瑰丽华尔兹
朴素dp:令 \(dp[i][x][y]\) 表示 \(i\) 时刻在 \((x,y)\) 的答案,初始是 \(0\) 时刻,转移很容易。
这个状态是很难优化的,\(i\) 和 \((x,y)\) 都不好拆开维护。考虑重设状态 \(dp[i][x][y]\) 表示第 \(i\) 个时间段在 \((x,y)\) 时的答案。转移是 \(dp[i][x][y]=\max(dp[i-1][x'][y']+dis)\),这个 \(dis\) 对不同的方向需要分讨。以当前时间段的方向向南为例,设这段时间长 \(len\),那么具体的转移就是 \(dp[i][x][y]=\max\limits_{p=x-len}^x(dp[i-1][p][y]+x-p)\),可以考虑将定值搬到 \(\max\) 外,写成: \(dp[i][x][y]=\max\limits_{p=x-len}^x(dp[i-1][p][y]-p)+x\)。这个时候已经可以发现,转移的范围就是一段长为 \(len\) 的连续的区间,可以用单调队列优化掉枚举 \(p\) 的过程。空间的话直接开是开得下的,也可以滚动数组优化掉 \(i\) 这一维。注意四个方向的转移顺序和转移式都不一样。
P3800 Power收集
我傻。直接就是滑动窗口,但是 \(j\) 在窗口的正中间。试过不能正反两次单调队列,于是考虑在开始对每一行开始dp前就把 \(1\sim T\) 的元素入队,然后不断加入 \(j+T\) 的元素,在加入元素的时候就顺便把该退役的元素给弹出了。
下面是几道树形背包。
P1272 重建道路
状态好设:\(dp[u][i]\) 表示在 \(u\) 子树中获得大小为 \(i\) 的子树的最小断边数。容易想到转移本质上是要在各个儿子的子树中分配留下的点数 \(s[v]\),使得每个儿子得到对应子树大小的价值之和 \(\sum c[v]\) 最小。将问题抽象成给若干个物品分配空间,每个物品的每种空间对应一种代价,要使得总代价最小。
可以看出是个树形背包,转移式就是 \(dp[u][j]=\min(dp[u][j]+1,dp[u][j-s_v]+dp[v][s_v])\),要枚举 \(u,j,s_v\),复杂度 \(O(n^3)\)。注意到因为压缩了状态,需要保证 \(dp[u][j]\) 比 \(dp[u][j-s_v]\) 先更新,所以考虑 \(j\) 倒序枚举,\(s_v\) 顺序枚举。最后的答案就是 \(dp[u][P]+1\),但如果 \(u=1\) 的话就不用加 \(1\),因为这个 \(1\) 的含义是断掉 \(u\) 和父亲的连边,这样才有大小为 \(P\) 的子树。
P2015 二叉苹果树
将边权转化成点权,设 \(dp[i][j]\) 表示 \(i\) 子树内保留 \(j\) 个点的最大价值。其实是和上个题真的差不多的树形背包板子,给个转移:
for(int j=k;j>0;--j)
for(int k=0;k<=min(siz[v],j-1);++k)
dp[u][j]=max(dp[u][j],dp[u][j-k]+dp[v][k]);
P4516 [JSOI2018] 潜入行动
设 \(dp[u][i][0/1][0/1]\) 表示在 \(u\) 子树内放 \(i\) 个监听器,且 \(u\) 有没有放设备和 \(u\) 有没有被覆盖。在多个儿子中枚举放的物品数量,明显是树形背包。然后开始按状态的含义推转移式,分讨:
这样就已经行了,反正我是不会独立推导。但是你这样式子写得又臭又长,错了的话很难调试。考虑怎么减少这一堆 \(0/1\) 带来的代码复杂度,一个想法是用循环来代替枚举,但我们还要考虑什么情况下能转移答案。
假设当前枚举到 \(dp[u][i][p1][q1],dp[v][j][p2][q2]\) ,要将他们转移到 \(dp[u][i+j][p3][q3]\) 中,考虑 \(p3,q3\) 具体的值是什么。结合实际意义观察上面式子能发现 \(p3=p1,q3=q1|p2\),但同时注意到在实际意义中我们需要满足 \(v\) 一定会被其子树或 \(u\) 覆盖,所以还要保证 \(p1|q2=1\) 才能转移。于是就可以新开一个数组,然后用 for 来代替手动转移了,不容易出错。
同时这题还有个难点就是复杂度分析。按我们上面说的枚举 \(u,i,j\) 感觉上是 \(O(nk^2)\) 的,过不了。但其实通过严格控制转移上界就是 \(O(nk)\) 的,简单理解就是我们每次都会限制枚举点数的上界不超过 \(k\),也就是 \(i+j\) 的上界是 \(k\),而我们外层枚举了 \(i\),内层的 \(j\) 的上界就是 \(k-i\),这样转移的次数就不会超过 \(O(\frac{n}{k})\),所以总的复杂度就是 \(O(nk)\) 的,附带一个 \(16\) 的常数。
(其实树形背包都是 \(O(n^2)\) 的)
两个坑点:卡空间,只能开 int;要严格处理转移上界 \(\le k\),不能直接拿子树大小,不然会 TLE。这题确实理解到了。
P1273 有线电视网
直接求人数不好做,考虑设 \(dp[u][j]\) 为 \(u\) 子树中选 \(j\) 个叶子的最大收益,转移是树形背包板子,最后统计答案找到最大的 \(j\) 满足 \(dp[1][j]\ge 0\) 就行了。
P3874 [TJOI2010] 砍树
01分数规划。要求一组 \(f_i\in\{0,1\}\) 使得 \(\dfrac{\sum v_i\times f_i}{\sum w_i\times f_i}\) 最大,现在已经二分出答案 \(mid\),转化判定式:
到了这里,我们就把每个物品的价值转化成了 \(v_i-mid\times w_i\),这样就可以愉快的当树形背包板子来打了,复杂度 \(O(n^2\log V)\)。需要注意的是二分时的精度不要只精确到 \(0.01\),要多精确两位到 \(0.0001\)。
P4322 [JSOI2016] 最佳团体
和上面一模一样的题,但是注意答案必须取 \(dp[0][k+1]\),必须包含自己。
P3177 [HAOI2015] 树上染色
套路题。考虑对每条边算贡献,一条边的贡献就是它两边的黑点个数乘积 \(+\) 白点个数乘积。转移式:
注意 \(k\in[j+siz[v]-siz[u],\min(siz[v],j)]\),这样转移才不会出错。
P4037 [JSOI2008] 魔兽地图
问题就很像树形背包,但更复杂。首先由于题目多了“合成”这一条件,所以我们要在状态中多设一维(这个状态我就不会了谔谔),令 \(f[u][j][k]\) 表示 \(u\) 子树中选出 \(j\) 个 \(u\) 点且总共花 \(k\) 块钱的答案。
由易到难考虑。首先我们在过程中计算出每个点最多能买的个数作为转移上界。考虑转移,对于叶子的初始化是简单的,枚举买的个数 \(j\) 和用来合成的个数 \(k\),\(f[u][j][k\times b_u]=a_u\times(j-k)\)。
对于其它节点,我们再记一个 \(g[j][k]\) 表示买了 \(j\) 个 \(u\) 点,共用了 \(k\) 块钱且不计 \(u\) 点贡献的最大价值,用于辅助转移。枚举买的个数 \(j\),总钱数 \(k\),儿子 \(v\) 中花费的钱数 \(l\),同时合成 \(u\) 需要 \(w\) 个 \(v\),转移:\(g[j][k]=\max(g[j][k-l]+f[v][j\times w][l])\)。注意直接数组记录可能会影响答案,要另开一个变量记录最大值。最后的树形背包转移,枚举总共有 \(i\) 个 \(u\),\(j\) 个 \(u\) 用于合成,花了 \(k\) 块钱:\(f[u][j][k]=\max(g[i][k+(i-j)\times a[u])\)。统计总答案的话可以考虑建一个 \(0\) 号点,也可以直接背包求答案。令 \(ans[m]\) 记录 \(m\) 块钱最大能得到的答案,枚举每个树的根 \(i\),转移就是 \(ans[j]=\max(ans[j-k]+f[i][0][k])\)。
MZOJ #1047. 划分
我会朴素dp,对 \(a\) 做前缀和转移: \(dp[i]=\max(dp[i],\min(dp[j],a[i]-a[j]+b[j+1]+c[i]))\)。复杂度 \(O(n^2)\)。拆式子不好拆,换一个角度思考。这个题本质上就是求 \(a[i]-a[j]+b[j+1]+c[i]\) 的最大的最小值,既然求的是最大的最小值,自然想到二分答案,然后判断是否能得到当前二分到的答案。这样我们就不断找到是否存在这么一个段就行了。具体来说:
res=a[1]+b[1];
for(int i=2;i<=n;++i){
if(res+c[i-1]>=mid&&b[i]>res) res=b[i];
res+=a[i];
}
res+=c[n];
MZOJ #1070.纵使日薄西山(xor)
将枚举四个数转化成枚举两对数 \((a_1,b_1),(a_2,b_2)\) 使得异或和相等。\(O(n^2)\) 枚举所有点对,用桶记录每个异或和的个数,加上贡献。但是这样会把 \((a_1,b_2),(a_2,b_1)\) 和 \((a_1,a_2),(b_1,b_2)\) 的贡献也算一次,所以要把答案除以 \(3\)。题目给了一个 \(m\),所以在 \(O(n^2)\) 的循环中判断当前答案是否超过 \(m\),直接退出即可。也可以FWT,但我不会。
MZOJ #1076. room
考虑分讨选择的两个障碍的位置情况。第一种是删了一个障碍起终点就连通了,第二种是删除两个相邻的障碍后联通,第三种是删除两个障碍物后使 \((1,1),(n,m)\) 与一个连通块 \(C\) 联通。一二种情况可以直接从 \((1,1),(n,m)\) 跑dfs,然后分讨能否到达就行了。第三种考虑并查集维护连通块,细节较多。具体来说,我们枚举 \((1,1)\) 能到达的障碍和 \((n,m)\) 能到达的,看他俩在不在一个连通块就行了,注意每次要还原并查集。
MZOJ #1074. swap
总结为自己傻逼想不到。因为 \(k\le 10^{16}\),所以当把大数放到倒数 \(\log_{10}k\) 位前一定是赚的。所以可以直接排序把大数放到前面,而最后的十几位直接用 \(O(n^2)\) 的做法就好了。
错因:不知道为什么脑子错乱了没想到把大数放到前面一定更优。
P2470 [SCOI2007] 压缩
这种压缩区间的题显然是区间dp,不用考虑在一个状态中压缩多次。设 \(dp[i][j]\) 表示 \([i,j]\) 的最短长度,枚举断点,如果 \(s_{i\sim k}=s_{k+1\sim j}\),那么转移并加上多出的 M 和 R。但是这样错了,题目描述的是 R 重复从上一个 M 开始的子串,也就是如果dp出来的结果是 \(\text{MaMbRR}\) 的话就是不合法的,第二个 R 并不会匹配第一个 M。考虑重设状态 \(dp[i][j][0/1]\) 表示 \([i,j]\) 内有无 M 时的答案。我们可以默认每一个状态的 \(i-1\) 位上都有一个 M,这样符合题意且方便转移:
枚举断点,第一行的具体含义是因为 \(i-1\) 处有 M,所以可以且只可压缩 \([i,k]\),右半边就直接原样加上。第二行是在 \(k,k+1\) 间插入一个 M,这样左右半边都可以压缩。
还有一种情况是区间可以直接压缩,直接哈希判断后 \(dp[i][j][0]=dp[i][mid][0]+1\) 就行了。
P2679 [NOIP2015 提高组] 子串
朴素dp设 \(dp[i][j][k]\) 表示 \(A\) 前 \(i\) 个字符与 \(B\) 前 \(j\) 个字符匹配且分了 \(k\) 段的方案。先继承 \(dp[i-1][j][k]\),再枚举 \(l\) 满足 \(A_{i-l\sim i}=B_{j-l\sim j}\),加上 \(dp[i-l-1][j-l-1][k-1]\),实际意义是枚举以 \(i\) 为结尾的第 \(k\) 个子串,转移了这个子串的起点前的答案。
发现第二种转移的范围是连续的,于是可以考虑对 \(dp[i-l]\) 用前缀和维护,只要中间有一个不匹配, 那么之前的贡献对于之后就无效了。于是记 \(s[i][j][k]\) 为对于 \(A_i,B_j\) 向前扩展的所有贡献。同时前缀和优化后 \(i\) 只和 \(i-1\) 有关,所以可以用滚动数组优化空间。
P10194 [USACO24FEB] Milk Exchange G
考虑对每个点找到
妈的我在干什么
P2986 [USACO10MAR] Great Cow Gathering G
一眼简单换根,这种题还是能秒的:\(dp[v]=dp[u]-(siz[v]\times w)+(tot-siz[v])\times w\)
P1850 [NOIP2016 提高组] 换教室
不难,设 \(dp[i][j][0/1]\) 表示前 \(i\) 个课换了 \(j\) 次教室,第 \(i\) 个换不换的答案,不设最后一维无法转移。而转移也不难想:
其中 \(V1,V2,V3,V4\) 是对应情况的期望贡献,也就是距离 \(\times\) 概率,两两间最短路一遍Floyd求出,然后注意期望不要算错即可。
P1156 垃圾陷阱
水题,但人傻了。这个有点像背包,考虑把生命这一维作为状态表示的值,那么设 \(dp[j]\) 为当高度为 \(j\) 时的最大生命值,第一维枚举物品的 \(i\) 显然可以滚掉。当 \(dp[j]\) 不小于当前枚举到的物品出现的时间就能填表转移:\(dp[j+h_i]=\max(dp[j]),dp[j]+=f_i\)。注意如果这时的 \(j+h_i\) 已经大于 \(m\) 了就直接输出,因为我们提前对物品按时间排序了。最后如果出不去的话那么肯定是一直加血,直接输出 \(dp[0]\) 就行。
P2607 [ZJOI2008] 骑士
容易想到这是个基环树森林上的最大权独立集问题,对于树上的答案可以一遍dp求得,这个很简单。对于基环树考虑找到多出的那条边,记录其两端点为 \(s,t\),分别作为根进行dp,如果遇到了多出的边就忽略,最后取 \(\max(dp[s][0],dp[t][1])\)。直接取 \(dp[s][0]\) 是因为 \(s,t\) 不能同时取,所以肯定有其中一个取不了。虽然这个里有有点废话,但是感性理解也确实说得过去。
MZOJ #1083.物流(logistics)
边数是 \(O(n^2)\) 级的,太多了,发现数据支持 \(O(nq)\) 的做法,于是考虑怎么减少边数到 \(O(n)\) 级。每次查询相当于是增加了一条边,可以想不到离线下来,先求出初始的最小生成树的边,然后把增加的边加进去,每次询问直接跑kruskal,在过程中判断这条边在时间上是否能选择就完了,边数是 \(n-1+q\)。很简单的,但是傻逼出题人卡常,所以第一遍边数 \(O(n^2)\) 的时候要用prim。
P4158 [SCOI2009] 粉刷匠
以前的自己好菜啊,这种简单题都不会做。如果只有一维的话,直接设 \(dp[i][j]\) 表示前 \(i\) 个格子涂了 \(j\) 次的答案,因为不会重复涂,所以容易得到转移是: \(dp[i][j]=\max(dp[k][j-1]+\max(S_0,S_1))\),\(S0,S1\) 是 \([k+1,i]\) 的 \(0/1\) 数。
有多行?直接把上面的数组改成 \(f[i][j][k]\) 记第 \(i\) 行前 \(j\) 个刷 \(k\) 次的答案,然后再记 \(g[i][j]\) 表示前 \(i\) 行刷 \(j\) 次的答案,\(g[i][j]=\max(g[i-1][j-k]+f[i][m][k])\),然后取全局最大值就没了。求 \(f\) 复杂度 \(O(n^2m^2)\),求 \(g\) 复杂度 \(O(nmT)\),注意求 \(g\) 的时候 \(k\) 的上界是 \(\min(j,m)\),不要越界。
P1772 [ZJOI2006] 物流运输
想到记录 \(val[i][j]\) 表示 \([i,j]\) 天中不变的最短路的长度就简单了。可以设 \(dp[i]\) 记录前 \(i\) 天的答案,转移更简单 \(dp[i]=\max(dp[j]+(i-j)\times val[j+1][i]+k)\)。注意 \(dp[i]\) 的初值是 \(val[1][i]\times i\)。求出 \(val[i][j]\) 直接枚举 \(i,j\) 然后标记不能走的点跑最短路就完了。注意 \(dp\) 开long long。
P3554 [POI2013] LUK-Triumphal arch
真不难,应该认真思考的。二分答案是显然的,首先贪心地想到逐层覆盖的策略,但因为每次操作都是 A 先手所以这是假的,一颗满二叉就hack了。
但是还是能得到一个策略:每次覆盖都尽量覆盖完一个子树内深度相同的点,如果次数不够就肯定要父亲分覆盖次数下来,称这个额外次数为 \(u\) 的代价。
根据这个,可以设 \(dp[u]\) 表示 \(u\) 子树中(不含 \(u\))的总代价。转移是明显的:\(dp[u]=cnt_u+\sum dp[v]\),\(cnt_i\) 是儿子的个数。最后如果 \(dp[1]\le0\) 那么就说明当前 \(mid\) 合法。注意如果 \(dp[v]\ge 0\) 我们才会转移,毕竟 \(v\) 的子树将多的次数给 \(u\) 的其他儿子的子树中,但是 \(cnt_u\) 是要的。
P10653 「ROI 2017 Day 2」存储器
先考虑 \(70\text{pts}\) 部分分,考虑把极长连续段先缩起来,然后用栈维护新加入的元素和栈顶的关系,如果符号相同就合并,加号比减号多也合并,\(O(n)\) 解决。发现对于 \(T\) 中的每个机场连续段,他只可能由 \(S\) 中对应位置的符号转变来,不会被其它段影响。所以可以直接对每个极长段都跑一遍 \(70\) 分的做法就行了,均摊下来还是 \(O(n)\) 的。
注意还要判断初始时 \(S\) 和 \(T\) 的极长连续段能不能对上,具体来说是 \(T\) 的某一极长段为 \([l,r]\),则必须满足 \(S_l\neq S_{l-1},S_r\neq S_{r+1},S_l=T_l,S_r=T_r\),这样可以限制贪心合并的合法性,参考 ++-+-- +++---。
P8865 [NOIP2022] 种花
先考虑 C 形,容易想到枚举点作为 C 形的左上角,如果确定了两横的行,那么以这个点为左上角的 C 的个数就是连续的 \(0\) 数量减一的乘积 \((len_i-1)\times (len_j-1)\),这个可以通过预处理每一个点最右能扩展到的 \(0\) 的位置得到。令确定的点为 \((i,j)\),那么答案就是 \(\sum\limits_{k=i+2}^{lim} (len_i-1)\times (len_k-1)\),\(lim\) 就是 \((i,j)\) 在这一列最下能扩展到的位置。 显然可以改写 \((len_i-1)\times\sum\limits_{k=i+2}^{lim} (len_k-1)\),直接前缀和优化。
考虑将 C 形拓展到 F 形,发现 F 就是 C 在第二行下面又多了几个格子,答案变为 \((len_i-1)\times\sum\limits_{k=i+2}^{lim-1} (len_k-1)\times(lim-k)\),也是直接前缀和优化就完了。注意此时 \(k\) 的上界是 \(lim-1\)。
P1073 [NOIP2009 提高组] 最优贸易
显然先把强连通分量缩起来建新图,对每个连通分量先求出最大最小的 \(a_i\),然后考虑以拓扑排序的方法在 DAG 上dp,在遍历过程中更新每个分量前面最小的 \(a_i\),然后转移 \(dp[v]=\max(dp[v],dp[u],mx[v]-mn[v])\)。注意这个人是从 \(1\) 开始走到 \(n\),所以能更新 \(v\) 的信息当且仅当 \(u\) 已经遍历到能被 \(1\) 到达,开个数组记录即可。
P1841 [JSOI2007] 重要的城市
你要记住一个trick:类似于“一个点是否必要/删掉之后对最短路有没有影响”的问题考虑记录到达每个点的最短路方案数,例子:如果 \(cnt_{1,u}\times cnt_{u,n}=cnt_{1,n}\),那么 \(u\) 必定在 \(1\sim n\) 的最短路上。知道了这个就好做了,考虑在Floyd过程中记录 \(i\) 到 \(j\) 的最短路个数,这是好维护的。统计答案时如果一个 \(k\) 满足 \(dis_{i,k}+dis_{k,j}=dis_{i,j}\) 且 \(cnt_{i,k}\times cnt_{k,j}=cnt_{i,j}\),那么这个 \(k\) 就一定在 \(i\) 到 \(j\) 的最短路上,也就是删去 \(k\) 后会对 \(dis_{i,j}\) 产生影响。

 挣扎
挣扎

 浙公网安备 33010602011771号
浙公网安备 33010602011771号