4月の题

CF1956C

赛时整的太他妈复杂了，没做处理，炸了。
下次做C的时候真别想得太复杂，特别是这种构造题，如果代码到2kb左右了那大概率就是想复杂并且错了。
但是还是我自己傻逼。

最优方案是长这样的：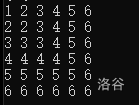
这样可以使小的数的数量尽量小，大的数的数量尽量大，构造方式：从 \(n\) 开始往前，横着放一个 \(\mathbf{1}\sim n\) 排列，再竖着放一个，没了，想不出来怪你自己。

CF1956D

还没看懂，待补。

CF1954D

计数题，考虑dp。

CF946G

先考虑没有去掉一个元素的条件怎么做。因为是删除元素，那么可以考虑找一个最长不下降子序列，这个子序列以外的元素就必定是要删去的。
但是直接这样找肯定是假的，我们考虑对于一个下降子序列中的元素 \(a_i\ge a_j\)，其一定满足 \(a_i-a_j\ge i-j\)，即 \(a_i-i\ge a_j-j\)。那么就把原序列的每个 \(a_i\) 转化成 \(a_i-i\) 然后找最长不下降子序列。
然后考虑加上删去一个数的条件，可以枚举删除点然后将左右两部分的答案拼起来，或者重新设计状态，设 \(dp[i][\mathbf{0/1}]\) 表示以第 \(i\) 个元素结尾，且前 \(i\) 个中有/无额外删除的元素时的答案。
\(dp[i][\mathbf{0}]=\mathtt{max}_{j<i,a_j-j\le a_i-i}\{dp[j][\mathbf{1}]+\mathbf{1}\},dp[i][\mathbf{1}]=\mathtt{max}\left\lbrace {\mathtt{max}_{j<i,a_j-j\le a_i-i}\{dp[j][\mathbf{1}]+\mathbf{1}\}} \atop {\mathtt{max}_{j<i-\mathbf{1},a_j-j\le a_i-i+\mathbf{1}}}\{dp[j][\mathbf{0}]+\mathbf{1}\}\right\rbrace\)
这 \(LaTeX\) 怎么这么傻逼，不写了，淦。

之后把主题换了得了。

CF1753D

首先找点性质，可以发现，移动完之后的每一张椅子都至少有一端是在最初的位置的，感性理解一下就是两端都动的前提是有个 \(\mathbf{1}\times \mathbf{2}\) 的空位，但是不移动肯定是更优的。
这样每张椅子都只可能平移一格或转九十度，那么只需找到最小的 \(w(i,j)+w(i+\mathbf{1},j)\) 或 \(w(i,j)+w(i,j+\mathbf{1})\) 就行了。考虑建一个源点 \(s\)，向所有空地连权值为 \(\mathbf{0}\) 的边，每个 \(L,R,U,D\) 就分别连两个转 \(\mathbf{90}°\) 到达的格子和一个转 \(\mathbf{180}°\) 到达的格子表示平移一格所代表的点，然后跑最短路就行了，最后每个点的答案答案就是 \(dis\)。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define mk make_pair
const ll N=3*114514,M=1919810,inf=1e18,mod=998244353;
struct xx{
	ll next,to,val;
}e[2*M];
ll head[2*M],cnt;
void add(ll y,ll x,ll z){
	e[++cnt].next=head[x];
	e[cnt].to=y;
	e[cnt].val=z;
	head[x]=cnt;
}
char c[N];
ll n,m,P,Q,s,t;
ll dis[N],vis[N];
typedef pair <ll,ll> pi;
priority_queue <pi,vector<pi>,greater<pi> > q;
ll id(ll i,ll j){return (i-1)*m+j;} //屮了又是这里 
void dij(){
	for(int i=1;i<=n*m+1;++i) dis[i]=inf,vis[i]=0;
	dis[s]=0;
	q.push(mk(dis[s],s));
	while(!q.empty()){
		ll u=q.top().second; q.pop();
		if(vis[u]) continue;
		vis[u]=1;
		for(int i=head[u];i;i=e[i].next){
			ll v=e[i].to,w=e[i].val;
			if(dis[v]>dis[u]+w){
				dis[v]=dis[u]+w;
				q.push(mk(dis[v],v));
			}
		}
	}
}
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin>>n>>m>>P>>Q;
	for(int i=1;i<=n;++i)
		for(int j=1;j<=m;++j)
			cin>>c[id(i,j)];
	s=0;
	for(int i=1;i<=n;++i)
		for(int j=1;j<=m;++j){
			ll uid=id(i,j);
			if(c[uid]=='.') add(uid,s,0);
			if(c[uid]=='L'){
				if(i>1&&c[id(i-1,j+1)]!='#') add(uid,id(i-1,j+1),P);
				if(i<n&&c[id(i+1,j+1)]!='#') add(uid,id(i+1,j+1),P);
				if(j+1<m&&c[id(i,j+2)]!='#') add(uid,id(i,j+2),Q);
			}
			if(c[uid]=='R'){
				if(i>1&&c[id(i-1,j-1)]!='#') add(uid,id(i-1,j-1),P);
				if(i<n&&c[id(i+1,j-1)]!='#') add(uid,id(i+1,j-1),P);
				if(j-1>1&&c[id(i,j-2)]!='#') add(uid,id(i,j-2),Q);
			}
			if(c[uid]=='U'){
				if(j>1&&c[id(i+1,j-1)]!='#') add(uid,id(i+1,j-1),P);
				if(j<m&&c[id(i+1,j+1)]!='#') add(uid,id(i+1,j+1),P);
				if(i+1<n&&c[id(i+2,j)]!='#') add(uid,id(i+2,j),Q);
			}
			if(c[uid]=='D'){
				if(j>1&&c[id(i-1,j-1)]!='#') add(uid,id(i-1,j-1),P);
				if(j<m&&c[id(i-1,j+1)]!='#') add(uid,id(i-1,j+1),P);
				if(i-1>1&&c[id(i-2,j)]!='#') add(uid,id(i-2,j),Q);
			}
		}
	dij();
	ll ans=inf;
	for(int i=1;i<=n;++i)
		for(int j=1;j<=m;++j){
			ll uid=id(i,j);
			if(c[uid]=='#') continue;
			if(i<n&&c[id(i+1,j)]!='#') ans=min(ans,dis[uid]+dis[id(i+1,j)]);
			if(j<m&&c[id(i,j+1)]!='#') ans=min(ans,dis[uid]+dis[id(i,j+1)]);
		}
	if(ans==inf) cout<<-1;
	else cout<<ans;
	return 0;
}//我服了爸爸