二月の题
为什么会有文化课寒假作业???
P5046 [Ynoi2019 模拟赛] Yuno loves sqrt technology I
傻逼卡常题去似吧
强制在线考虑分块。先把区间的贡献给拆开,珂以拆成下面图的形式:

其中绿色是整块内部的贡献,橙色是单个散块内部贡献,蓝色是散块对散块的贡献,红色是散块和整块之间的贡献。考虑分开来处理四个部分。
橙色部分,单个块的贡献考虑用树状数组求出逆序对,没啥好说,注意我们后面要维护前后缀和的时候注意树状数组加减值是什么以及加减的顺序。
绿色珂以预处理一个 \(sum\) 表示 \(i\) 到 \(j\) 块的贡献,处理这个珂以先记录每个块中小于等于 \(x\) 的数的个数,然后对这个做块之间的前缀和,处理的时候假设左块为 \(i\) 右块为 \(j\),对于 \(j\) 块的每一个数差分出前面比它大的数的个数,求和,最后加上 \(j\) 块内部的贡献还有 \(sum[i][j-\mathbf{1}]\)。
蓝色可以考虑新开一个数组赋值原数组,然后对这个数组在每个块内从小到大排序,还要按他原来的位置排。查询的时候就两个单调指针往后扫,如果指的数原下标不在查询区间内就跳过,左边指的数小于右边的就左边指针跳,否则右边的一直跳,贡献是左边剩下的有效的数,具体细节看代码。
红色部分考虑我们前面记录的 \(cnt\mathtt{2}\) 也就是每个块中小于等于 \(x\) 的数的个数,块之间的前缀和。直接枚举左右散块的数然后对中间整块差分就行了。
但是毒瘤 \(\mathtt{lxl}\) 他妈就喜欢卡常,这代码是对的,但是思路和实现还是太繁琐了,之后有时间再来写吧。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define in inline
const ll N=100100,M=400;
struct xx{
ll val;
int id;
}b[N];
in bool cmp(xx x,xx y){
return x.val==y.val?x.id<y.id:x.val<y.val;
}
int n,m;
ll a[N];
int ns,nq,st[400],ed[400],bel[N];
ll sum1[400][400],sum2[400][N],sum3[400][N];
int sum[N];
//i~j整块贡献、每个块逆序对数前缀/后缀和
int cnt1[400][N];
ll cnt2[400][N];
int c[N];
//cnt1每个块内小于等于j的数的个数,cnt2是cnt1块间前缀和
in int lowbit(int x){return x&-x;}
in void update(int x,int k){
while(x<=n){
c[x]+=k;
x+=lowbit(x);
}
}
in int query(int x){
int ans=0;
while(x){
ans+=c[x];
x-=lowbit(x);
}
return ans;
}
int c1[350],c2[350];
in ll calc(ll l,ll r){
if(l>r) return 0ll;
ll ans=0; int lx=bel[l],rx=bel[r];
if(lx==rx){
ans=sum2[rx][r]-sum2[lx][l-1];
int t1=0,t2=0;
for(int i=st[lx];i<=ed[lx];++i)
if(b[i].id<l) c1[++t1]=b[i].val;
else if(b[i].id<=r) c2[++t2]=b[i].val;
for(int i=1,j=1;i<=t1;++i){
while(j<=t2&&c1[i]>c2[j]) ++j;
ans-=j-1;
}
return ans;
}
ans+=sum2[rx][r]+sum3[lx][l]; //散块内部贡献
int j=st[rx],i_cnt=0,i_n=ed[lx]-l+1;
for(int i=st[lx];i<=ed[lx];++i){ //散块之间贡献
if(b[i].id<l) continue;
++i_cnt;
while(j<=ed[rx]&&b[j].val<b[i].val){
if(b[j].id<=r) ans+=i_n-i_cnt+1;
++j;
}
}
if(rx>lx+1){
ll siz=ns*((rx-1)-(lx+1)+1);
for(int i=l;i<=ed[lx];++i) ans+=cnt2[rx-1][a[i]]-cnt2[lx][a[i]];
for(int i=st[rx];i<=r;++i) ans+=siz-(cnt2[rx-1][a[i]]-cnt2[lx][a[i]]); //整散之间贡献
}
if(rx>lx+1) ans+=sum1[lx+1][rx-1]; //整块贡献
return ans;
}
int main(){
n=read(),m=read(); ns=260,nq=ceil(n*1.0/ns);
for(int i=1;i<=n;++i) a[i]=read(),b[i]=(xx){a[i],i};
for(int i=1;i<=nq;++i){
st[i]=ns*(i-1)+1,ed[i]=min(ns*i,n);
for(int j=st[i];j<=ed[i];++j){
bel[j]=i;
update(a[j],1);
sum[j]=(j-st[i]+1)-query(a[j]);
sum2[i][j]=sum2[i][j-1]+sum[j];
//散块内部贡献,每个块内逆序对数前缀和
++cnt1[i][a[j]];
}
for(int j=1;j<=n;++j) cnt1[i][j]+=cnt1[i][j-1],cnt2[i][j]=cnt2[i-1][j]+cnt1[i][j];
for(int j=st[i];j<=ed[i];++j) update(a[j],-1);
sort(b+st[i],b+ed[i]+1,cmp);
}
for(int i=1;i<=nq;++i){
for(int j=i;j<=nq;++j){
for(int k=st[j];k<=ed[j];++k){
ll siz=ns*((j-1)-i+1);
sum1[i][j]+=siz-(cnt2[j-1][a[k]]-cnt2[i-1][a[k]]);
}
sum1[i][j]+=sum1[i][j-1]+sum2[j][ed[j]];
}
for(int j=ed[i];j>=st[i];--j) update(a[j],1),sum[j]=query(a[j]-1);
for(int j=ed[i];j>=st[i];--j) update(a[j],-1),sum3[i][j]=sum3[i][j+1]+sum[j];
}
ll las=0;
for(int i=1;i<=m;++i){
ll x,y;
x=read(),y=read();
x^=las,y^=las;
las=calc(x,y);
write(las),putchar('\n');
}
return 0;
}
但我还是想骂人,妈的这题想了两天写加调了两天半最后他妈被卡常,淦,再也不做傻逼卡常题了/fn
P4099 [HEOI2013] SAO
淦忘记保存了。这个题多头写一个“求一个树的拓扑序数量”我还以为是啥水题,结果难得多。借鉴了一下。
考虑将有向图直接看成一颗树进行树形dp,设状态 \(dp[u][i]\) 表示在 \(u\) 的子树中 \(u\) 拓扑序上排名为 \(i\) 时的方案数。
考虑如何从儿子 \(v\) 转移到父亲 \(u\),我们珂以理解为是不断合并合并 \(u,v\) 子树的拓扑序。先初设 \(dp[u][\mathbf{1}]=\mathbf{1}\),先考虑 \(u\) 的排名在 \(v\) 前的限制情况,我们设合并前 \(u\) 的拓扑序排名为 \(i\),合并后有 \(j\) 个数排在 \(u\) 前面,\(v\) 的排名为 \(k\),感性理解一下怎么转移:我们现在要合并两个拓扑序序列,第一个序列中 \(u\) 在第 \(i\) 位,在第二个序列中 \(u\) 在第 \(k\) 位,要得出合并的方案数。将第二个序列也就是 \(v\) 的子树合并起来本身就是有组合方案的,即 \(v\) 子树插到 \(u\) 中的方案,组合数一部分是 \(C\binom{i+j-\mathbf{1}}{j}\),其组合意义是在拓扑序位于 \(u\) 前的 \(i+j-\mathbf{1}\) 个元素中选 \(j\) 个元素出来;另一部分则是拓扑序在 \(v\) 后的 \(siz[u]+siz[v]-i-j\) 个元素中放入剩下 \(siz[v]-j\) 个元素的方案,这样两者的积便是 \(C\binom{i+j-\mathbf{1}}{j}\times C\binom{siz[u]+siz[v]-i-j}{siz[v]-j}\)。考虑转移范围,显然 \(\mathbf{1}\le i\le siz_u,\mathbf{1}\le k\le siz_v\),因为做多有 \(k-\mathbf{1}\) 个 \(v\) 子树中元素在 \(u\) 前,所以 \(\mathbf{0}\le j<k\)。
于是我们令两者之积为一个常数 \(K\),珂以得到转移式:\(dp[u][i+j]+=dp[u][j]\times dp[v][k]\times K\),但是这个 \(dp[u][i]\) 是会被改变的,转移有后效性,所以我们珂以另开一个 \(tmp\) 记录下原来的 \(dp[u][i]\),并且要把 \(dp[u][i]\) 清零,然后代入转移。
\(u\) 排在 \(v\) 后面的情况也差不多,组合的方案是一样的,但是 \(v\) 已经在 \(u\) 前面了,所以 \(j\) 的范围是 \(k\le j\le siz_v\)。
然后考虑复杂度,要枚举 \(i,j,k\) 总共是 \(n^{\mathbf{3}}\) 的,过不了。考虑能不能将某一维转化成另一维,先将枚举转化为求和式,可以这样得到: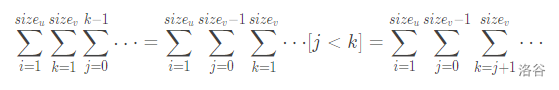
于是枚举 \(k\) 就被优化掉了,我们珂以把 \(dp[v][k]\) 提出来变为前缀和的形式,就将复杂度降至 \(O(n^{\mathbf{2}})\),可通过。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2005,M=1919810,mod=1e9+7;
struct xx{
ll next,to,fl;
}e[2*N];
ll head[2*N],cnt;
void add(ll x,ll y,ll z){
e[++cnt].next=head[x];
e[cnt].to=y;
e[cnt].fl=z;
head[x]=cnt;
}
ll T,c[N][N];
ll n,a[N],dp[N][N]; //u子树内排j时方案数
ll siz[N],tmp[N];
void dfs(ll u,ll fa){
siz[u]=1,dp[u][1]=1;
for(int i=head[u];i;i=e[i].next){
ll v=e[i].to,fl=e[i].fl;
if(v==fa) continue;
dfs(v,u);
for(int j=1;j<=siz[u];++j) tmp[j]=dp[u][j],dp[u][j]=0;
if(!fl){
for(int j=1;j<=siz[u];++j)
for(int k=0;k<=siz[v];++k)
dp[u][j+k]=(dp[u][j+k]+tmp[j]*(dp[v][siz[v]]-dp[v][k]+mod)%mod*
c[j+k-1][k]%mod*c[siz[u]+siz[v]-j-k][siz[v]-k]%mod)%mod;
}
else{
for(int j=1;j<=siz[u];++j)
for(int k=1;k<=siz[v];++k)
dp[u][j+k]=(dp[u][j+k]+tmp[j]*dp[v][k]%mod*
c[j+k-1][k]%mod*c[siz[u]+siz[v]-j-k][siz[v]-k]%mod)%mod;
}
siz[u]+=siz[v];
}
for(int i=1;i<=siz[u];++i) dp[u][i]=(dp[u][i]+dp[u][i-1])%mod;
}
void solve(){
memset(dp,0,sizeof(dp));
memset(head,0,sizeof(head));
cnt=0;
cin>>n;
for(int i=1;i<n;++i){
ll a,b; char ch;
cin>>a>>ch>>b; ++a,++b;
if(ch=='<') add(a,b,1),add(b,a,0);
else add(a,b,0),add(b,a,1);
}
dfs(1,0);
cout<<dp[1][n]<<'\n';
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
for(int i=0;i<=2000;++i) c[i][0]=c[i][i]=1;
for(int i=1;i<=2000;++i)
for(int j=1;j<=i;++j)
c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod;
cin>>T;
while(T--) solve();
return 0;
}
CF1743E
贪心不太行,考虑dp。首先同时开炮肯定是更优的,能少减去一个 \(s\)。同时看到充能的时间很大但是攻击力很小,所以考虑设 \(dp[i]\) 表示造成 \(i\) 点伤害所需的最小时间(包含防御力减去的)。我们先枚举 \(i\),然后枚举两个炮的攻击次数,记为\(\mathbf{s1},\mathbf{s2}\)。接着考虑贪心策略,我们发现如果要同时开炮的话可能会使一个炮充好能之后等待,而如果中间有时间发射再充能的话明显更优,我们就考虑比较两个炮的充能时间然后时间较少的炮多发射一次,不断循环这个操作,直到能造成的伤害大于等于 \(h\),这样可以保证任何一个时刻两个炮都不会都是空闲。转移式:\(dp[\mathtt{min}(i+p,h)]=\mathtt{min}(dp[\mathtt{min}(i+p,h)],dp[i]+t)\),\(p\) 是可造成伤害,\(t\) 是所用时间,复杂度 \(O(n^{\mathbf{2}})\)。
还要注意细节,一开始两者次数都是 \(\mathbf{0}\),我们要默认先增加充能时间小的炮的次数,要不然就珂能不优。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2*114514,M=1919810,inf=1e18;
ll p1,t1,p2,t2,h,s;
ll dp[N]; //造成i伤害所需的最小时间
int main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin>>p1>>t1>>p2>>t2>>h>>s;
if(t1<t2) swap(p1,p2),swap(t1,t2);
for(int i=1;i<=h;++i) dp[i]=inf;
dp[0]=0;
for(int i=0;i<=h;++i){
ll s1=0,s2=0,p=0;
while(i+p<h){
//不能都空闲
if(s1*t1<s2*t2) ++s1;
else ++s2;
ll fl=(s1&&s2),t=max(s1*t1,s2*t2);
p=s1*p1+s2*p2-(s1+s2-fl)*s;
dp[min(i+p,h)]=min(dp[min(i+p,h)],dp[i]+t);
}
}
cout<<dp[h];
return 0;
}
AGC023F
交换贪心(Exchange Argument)例题,这个东西需要用到并查集和优先队列。我们开一个结构体用来存所需要的信息,并且重载 \(<,==\) 运算符,然后把除了 \(\mathbf{1}\) 的点都放到优先队列里,因为我们要把答案合并到 \(\mathbf{1}\) 上(\(\mathbf{1}\) 是根)。在合并过程中用并查集维护,不断更新每个结点的答案。
这题中,我们考虑一个贪心策略:尽量使序列接近 \(\mathbf{\small{0}},\mathbf{\small{0}},\mathbf{\small{0}},\ldots,\mathbf{\small{1}},\mathbf{\small{1}},\mathbf{\small{1}}\),这样没有逆序对。我们考虑记录每个点的 \(\mathbf{0,1}\) 个数,这些点会合并成多个连通块。判断小于便是 return c1*x.c0>c0*x.c1;,然后用优先队列不断取队首然后和它的已经被合并的祖先合并就行了,每次合并答案加上 \(v.\mathbf{cnt1}*u.\mathbf{cnt0}\),注意还是不要把 \(\mathbf{1}\) 放进队列。最后输出 \(\mathbf{1}\) 的答案。
注意我们每次合并完一个儿子不能直接丢掉父亲,他还有别的儿子,但这样因为合并后会产生新的点,所以要特判目前的点是不是合并过的。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2*114514,M=1919810;
ll n,fa[N],a[N],f[N];
ll find(ll x){return x==f[x]?x:f[x]=find(f[x]);}
bool vis[N];
struct xx{
ll c1,c0,id,ans;
bool operator <(const xx &x)const{
return c1*x.c0>c0*x.c1;
}
bool operator ==(const xx &x)const{
return (c1==x.c1)&&(c0==x.c0);
}
bool operator !=(const xx &x)const{
return (c1!=x.c1)||(c0!=x.c0);
}
}b[N];
priority_queue <xx> q;
ll ans=0;
int main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin>>n;
for(int i=2;i<=n;++i) cin>>fa[i];
for(int i=1;i<=n;++i){
cin>>a[i];
b[i].id=i,f[i]=i;
if(a[i]) b[i].c1++;
else b[i].c0++;
if(i!=1) q.push(b[i]);
}
while(!q.empty()){
xx u=q.top(); q.pop();
if(find(u.id)!=u.id||b[u.id]!=u) continue;
ll v=find(fa[u.id]);
f[u.id]=v;
b[v].ans+=u.ans+b[v].c1*u.c0;
b[v].c0+=u.c0,b[v].c1+=u.c1;
if(v!=1) q.push(b[v]);
}
cout<<b[1].ans;
return 0;
}
P8360 [SNOI2022] 军队
看到鬼畜操作考虑分块。先考虑如果没有修改颜色的操作怎么做:很简单,整块维护加法 \(tag\) 和块中每个 \(x\) 的个数,修改时散块暴力加整块加 \(tag\) 就行了。
然后考虑怎么解决改颜色的问题,这里引入一个 trick:值域并查集,在最初分块和第二分块中都有用到。简单来说就是用并查集维护值域不大的信息。思路比较容易:我们初始记录下每个并查集里的元素个数 \(siz\)、父亲 \(fa\)、加法标记 \(tag\) 和这个并查集的颜色 \(col\),我用了个结构体存。先搞 find 怎么写,我们考虑记录跳到的点的编号 \(id\) 和当前点的 \(tag\),注意我们还是要路径压缩。我们顺便记录一个 \(sum\) 表示每个整块的权值和。
接下来考虑如何构建这个并查集:我们记录 \(f_i\) 表示对于原序列中的 \(i\) 它所属的并查集的编号,再记录 \(rt_{i,j}\) 表示在第 \(i\) 块中的所有颜色为 \(j\) 的元素所在的并查集编号。构建方式如下:
点击查看代码
for(int i=1;i<=nq;++i){
st[i]=ns*(i-1)+1,ed[i]=min(ns*i,n); //顺便把块分了,少点常数
for(int j=st[i];j<=ed[i];++j){
bel[j]=i,sum[i]+=a[j];
if(!rt[i][c[j]]){
rt[i][c[j]]=f[j]=++tot; //tot是新增并查集的编号
t[tot].fa=t[tot].tag=0;
t[tot].siz=1,t[tot].col=c[j];
}
else f[j]=rt[i][c[j]],++t[f[j]].siz;
}
}
然后考虑修改颜色的操作。我们先考虑如何修改散块:我们直接遍历散块,直接对每一个元素进行 find,设得到的点编号为 \(p\),其加法标记为 \(val\),如果并查集的 \(p\) 点颜色不为 \(x\) 就直接跳过。否则就将 \(p\) 的 \(siz\) 减一,如果减一后 \(siz=\mathbf{0}\) 那么要清零: rt[bel[i]][t[p].col]=0。然后 \(a_i\) 加上所得权值,而且注意,如果修改成的颜色 \(y\) 初始不存在,那么要在并查集里新给它开一个点,不能直接放在原来的 \(x\) 的点上,同时如果 \(y\) 在并查集里那么 \(a_i\) 要减去 t[f[i]].tag,还有改大小这些比较显然的操作。
考虑对整块修改颜色,其实很简单,我们先取出两个颜色在并查集中的点,令 p1=rt[i][x],p2=rt[i][y];,如果 \(p\mathbf{1}\) 为 \(\mathbf{0}\) 那么跳过,有就合并到 \(p\mathbf{2}\) 上,还有如果 \(p\mathbf{2}=\mathbf{0}\) 那么就直接改一下 \(p\mathbf{1}\) 的颜色并且 swap 一下两个 \(rt\) 就行了,具体来说如下:
点击查看代码
if(p2){
t[p2].siz+=t[p1].siz;
t[p1].fa=p2;
t[p1].tag-=t[p2].tag;
rt[i][x]=0;//这个要删了
}
else{
t[p1].col=y;
swap(rt[i][x],rt[i][y]);
}
然后其他操作就比较简单了。区间加的话就散块 find 一下,如果得到的点的颜色是 \(x\) 那么 \(a_i\) 和 \(sum[bel[i]]\) 都加上 \(k\),整块就直接把 \(rt[i][x]\) 提出来然后对并查集加 \(tag\),对 \(sum[i]\) 也加一下就行了。
查询的话也简单,散块每个点 find 一下,然后 ans+=a[i]+u.val+t[u.id].tag;,注意 t[u.id].tag 是不包含在 u.val 中的,整块直接加维护的 \(sum\) 就行了。
然后就做完了,也不需要卡常,不需要逐块处理,细节也还好,比某些煞笔卡常题美好多了。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define in inline
#define ll long long
const ll N=250005,M=1919810;
int n,m,C,tot;
int ns,nq,st[N],ed[N],bel[N];
ll a[N],sum[N];
int c[N],f[N],siz[N],rt[550][N]; //f单个点指向的根,rt每块每颜色的根
struct xx{
int fa,siz,col;
ll tag;
}t[M];
struct gx{
int id;
ll val;
};
in gx find(int x){
if(!t[x].fa) return (gx){x,0ll};
gx y=find(t[x].fa);
y.val+=t[x].tag;
t[x].fa=y.id,t[x].tag=y.val;
return y;
}
in void calc(int l,int r,int x,int y,int id){ //暴力修改散块颜色
for(int i=l;i<=r;++i){
gx u=find(f[i]);
int p=u.id; ll val=u.val;
if(t[p].col!=x) continue;
if(!(--t[p].siz)) rt[id][t[p].col]=0;
a[i]+=val+t[p].tag;
if(!rt[id][y]){
rt[id][y]=f[i]=++tot;
t[tot].fa=t[tot].tag=0;
t[tot].siz=1,t[tot].col=y;
}
else{
f[i]=rt[id][y];
a[i]-=t[f[i]].tag;
++t[f[i]].siz;
}
}
}
in void update1(int l,int r,int x,int y){
if(x==y) return;
if(bel[l]==bel[r]){
calc(l,r,x,y,bel[l]);
return;
}
calc(l,ed[bel[l]],x,y,bel[l]);
calc(st[bel[r]],r,x,y,bel[r]);
for(int i=bel[l]+1;i<bel[r];++i){
ll p1=rt[i][x],p2=rt[i][y];
if(!p1) continue;
if(p2){
t[p2].siz+=t[p1].siz;
t[p1].fa=p2;
t[p1].tag-=t[p2].tag;
rt[i][x]=0;//删了
}
else{
t[p1].col=y;
swap(rt[i][x],rt[i][y]);
}
}
}
in void update2(int l,int r,int x,ll k){
if(bel[l]==bel[r]){
for(int i=l;i<=r;++i){
gx u=find(f[i]);
if(t[u.id].col==x) a[i]+=k,sum[bel[l]]+=k;
}
return;
}
for(int i=l;i<=ed[bel[l]];++i){
gx u=find(f[i]);
if(t[u.id].col==x) a[i]+=k,sum[bel[l]]+=k;
}
for(int i=st[bel[r]];i<=r;++i){
gx u=find(f[i]);
if(t[u.id].col==x) a[i]+=k,sum[bel[r]]+=k;
}
for(int i=bel[l]+1;i<bel[r];++i){
ll p=rt[i][x];
if(!p) continue;
t[p].tag+=k,sum[i]+=t[p].siz*k;
}
}
in ll query(int l,int r){
ll ans=0;
if(bel[l]==bel[r]){
for(int i=l;i<=r;++i){
gx u=find(f[i]);
ans+=a[i]+u.val+t[u.id].tag;
}
return ans;
}
for(int i=l;i<=ed[bel[l]];++i){
gx u=find(f[i]);
ans+=a[i]+u.val+t[u.id].tag;
}
for(int i=st[bel[r]];i<=r;++i){
gx u=find(f[i]);
ans+=a[i]+u.val+t[u.id].tag;
}
for(int i=bel[l]+1;i<bel[r];++i) ans+=sum[i];
return ans;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin>>n>>m>>C; ns=sqrt(n),nq=ceil(n*1.0/ns);
for(int i=1;i<=n;++i) cin>>a[i];
for(int i=1;i<=n;++i) cin>>c[i];
for(int i=1;i<=nq;++i){
st[i]=ns*(i-1)+1,ed[i]=min(ns*i,n);
for(int j=st[i];j<=ed[i];++j){
bel[j]=i,sum[i]+=a[j];
if(!rt[i][c[j]]){
rt[i][c[j]]=f[j]=++tot;
t[tot].fa=t[tot].tag=0;
t[tot].siz=1,t[tot].col=c[j];
}
else f[j]=rt[i][c[j]],++t[f[j]].siz;
}
}
//写不来逐块处理/fn
for(int i=1;i<=m;++i){
int opt,l,r,x,y; ll k;
cin>>opt>>l>>r;
if(opt==1){
cin>>x>>y;
update1(l,r,x,y);
}
if(opt==2){
cin>>x>>k;
update2(l,r,x,k);
}
if(opt==3) cout<<query(l,r)<<'\n';
//debug();
}
return 0;
}//甚至不用加快读
CF1768F
一个非常妙的dp,大概是贪心想到优化策略减少转移然后搭配阈值分治,代码很简单,就很厉害。
首先朴素的 \(n^{\mathbf{2}}\) dp 是很容易写出的,设 \(dp_i\) 表示跳到 \(i\) 点的最小花费,转移:\(dp_i=\mathtt{min}(dp_i,dp_j+\mathtt{min}[i,j]\times(i-j)^{\mathbf{2}})\)。
然后考虑怎么优化。注意到这题的值域是 \(\le n\) 的,我们尝试来发掘一些性质。首先考虑能不能来优化一下转移次数,把那些不优的转移优化掉。我们设一段区间为 \([i,j]\),考虑如果这段区间是值得转移的,那么应该满足不存在一个 \([i,j]\) 中的 \(k\) 使得先跳 \((i,k)\) 再跳 \((k,j)\) 比直接跳 \((i,j)\) 更优,但是我们发现直接判断所有 \(k\) 不太现实,因为还会有 \((j-i)^{\mathbf{2}}\) 的存在,我们就不妨先不考虑它。这样我们就能发现,一对 \((i,j)\) 如果是值得跳的,那么 \(a_i\) 或 \(a_j\) 一定是这段区间里的最小值。
由于值域是 \(n\),考虑这个 \((j-i)^{\mathbf{2}}\) 的增长速率是会越来越大的,当两个点的距离大于 \(\sqrt{n}\) 时 \(a_i\) 再大也大不过,所以就可以直接转移中间的点,反正也不超过 \(\sqrt{n}\) 个。另外,考虑这样推一个区间是否值得转移,应该满足这个式子:\(minn\times len^{\mathbf{2}}\le n\times len\),移项得到 \(minn\le \dfrac{n}{len}\)。这样结合区间长度不超过 \(\sqrt{n}\) 可以得出当 \(len>\sqrt{n}\) 时 \(minn\le\sqrt{n}\)。
还有注意到这题的数据和时限能让 \(O(n\sqrt{n})\) 跑过。
那么我们珂以考虑根号分治。当 \((i-j)\le\sqrt{n}\),直接暴力转移就行了。当 \((i-j)>\sqrt{n}\) 时分别考虑 \(a_i,a_j\) 为最小值时怎么搞。当 \(a_j\) 最小时我们就记录所有 \(\le sqrt{n}\) 的数上一个出现的位置,直接枚举这些位置然后转移就行了。当 \(a_i\) 最小时,就向前枚举直到 \(a_j\le a_i\) 就 break,否则就一直转移就行了,然后均摊下来单次转移 \(\sqrt{n}\),总共就是 \(O(n\sqrt{n})\),珂过。
这个题主要就是考虑去优化朴素的dp,看哪些状态是值得转移的,不会被其它更优的状态替代。用贪心的思想来想。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=4*114514,M=1919810,inf=114514191981000000;
ll n,a[N],dp[N];
ll ns,nq,las[N]; //大于根号就不用管了吧
int main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin>>n; ns=ceil(n*1.0/sqrt(n));
for(int i=1;i<=n;++i) cin>>a[i],dp[i]=inf;
dp[1]=0,cout<<0<<" ";
las[a[1]]=1;
for(int i=2;i<=n;++i){
ll minn=a[i];
for(int j=i-1;j>=max(1ll,i-ns);--j){ //暴力转移
minn=min(minn,a[j]);
dp[i]=min(dp[i],dp[j]+(i-j)*(i-j)*minn);
}
for(int j=1;j<=ns;++j) //左端点j最小
if(las[j]) dp[i]=min(dp[i],dp[las[j]]+(i-las[j])*(i-las[j])*j);
if(a[i]<=ns){ //右端点a_i最小
for(int j=i-1;j>=1;--j){
if(a[j]<=a[i]) break;
dp[i]=min(dp[i],dp[j]+a[i]*(i-j)*(i-j));
}
}
las[a[i]]=i;
cout<<dp[i]<<" ";
}
return 0;
}
P1989 无向图三元环计数
为什么题单里都放这么智慧的题。
考虑一个朴素做法,枚举 \(i\) 点,再枚举 \(i\) 连边的 \(j\) 点,再枚举 \(j\) 连边的 \(k\) 点,判断 \(k\) 和 \(i\) 有没有连边并判断是否这个环重复计数,时间复杂度 \(O(nm^{\mathbf{2}})\) 过不了。
先说做法:我们考虑记录下每个点的度数,然后对于每条无向边,将其改为度数小的点连向度数大的点的有向边,如果度数相同就编号小的连向大的,判断就先标记所有 \(j\),然后判断 \(k\) 有没有标记就行了。这样建出来一个有向图就不用判断环是否重复计数,并且枚举的边数似乎减少了。结论:复杂度变成 \(n\sqrt{m}\) 了。我们来证明一下,其实本质上还是根号分治。
令 \(n,m\) 同阶,考虑每一条边对复杂度的贡献,现在有已经枚举了一条 \(u\) 连向 \(v\) 的边,接下来要处理 \(v\) 的出度,分情况讨论:如果 \(v\) 在原图上的度数不大于 \(\sqrt{m}\) 时,由于新图每个节点的出度不可能大于原图的度数,所以处理 \(v\) 的出度的复杂度为 \(O(\sqrt{m})\);如果度数大于 \(\sqrt{m}\),它能连向的点,也就是度数大于 \(\sqrt{m}\) 的点最多只能有 \(\sqrt{m}\) 个,所以处理单个这样的 \(v\) 复杂度也是 \(\sqrt{m}\)。总复杂度 \(O(m\sqrt{m})\),珂过。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2*114514,M=1919810,inf=1e18;
struct xx{
ll a,b;
}e[N];
vector <ll> g[N];
ll n,m,du[N],ans;
bool vis[N];
bool cmp(ll x,ll y){
return du[x]>du[y];
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;++i){
cin>>e[i].a>>e[i].b;
if(e[i].a>e[i].b) swap(e[i].a,e[i].b); //这个还是要加
++du[e[i].a],++du[e[i].b];
}
for(int i=1;i<=m;++i){
if(du[e[i].a]>du[e[i].b]) g[e[i].b].push_back(e[i].a);
else g[e[i].a].push_back(e[i].b);
}
//所以这题是随便连边,只要一大一小就行?
for(int i=1;i<=n;++i){
for(int j:g[i]) vis[j]=1;
for(int j:g[i])
for(int k:g[j])
if(vis[k]) ++ans;
for(int j:g[i]) vis[j]=0;
}
cout<<ans;
return 0;
}
P1967 [NOIP2013 提高组] 货车运输
鸽了一年半/qd
首先,这很明显是让你求一个最大生成树,那么直接建就行了。然后考虑怎么搞查询,既然我们已经搞出了最大生成树,那么求出两个点之间路径的权值就行了,那么怎么求呢?
有一个trick,是在找LCA的倍增过程中就能处理出答案。记录一个倍增数组 \(val[u][i]\),初始全赋成极大值,然后在 dfs 预处理中这样写:val[v][j]=min(val[v][j-1],val[f[v][j-1]][j-1]);。然后查询LCA时,用一个极大的 ans 不断在倍增过程中和 \(val[u][i]\) 取较小值,注意更新顺序,ans 要先更新。
还有样例和无解情况提醒了你这是一个森林。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2*114514,M=1919810,inf=1e18;
ll n,m,q;
struct edge{
ll u,v,w;
}a[N];
bool cmp(edge x,edge y){
return x.w>y.w;
}
struct xx{
ll next,to,val;
}e[2*N];
ll head[2*N],cnt;
void add(ll x,ll y,ll z){
e[++cnt].next=head[x];
e[cnt].to=y;
e[cnt].val=z;
head[x]=cnt;
}
ll fa[N],lg[N],dept[N],f[N][32],val[N][32]; //trick
bool vis[N];
ll find(ll x){
return x==fa[x]?x:fa[x]=find(fa[x]);
}
void dfs_pre(ll u,ll fa){
vis[u]=1;
for(int i=head[u];i;i=e[i].next){
ll v=e[i].to,w=e[i].val;
if(v==fa||vis[v]) continue;
dept[v]=dept[u]+1;
f[v][0]=u,val[v][0]=w;
for(int j=1;j<=lg[dept[v]];++j)
f[v][j]=f[f[v][j-1]][j-1],
val[v][j]=min(val[v][j-1],val[f[v][j-1]][j-1]); //牛
dfs_pre(v,u);
}
}
ll query_lca(ll a,ll b){
ll ans=inf;
//if(a==b) return a;
if(dept[a]<dept[b]) swap(a,b);
for(int i=lg[dept[a]];i>=0;--i)
if(dept[f[a][i]]>=dept[b])
ans=min(ans,val[a][i]),a=f[a][i];
//更新顺序反了,囸
if(a==b) return ans;
for(int i=lg[dept[a]];i>=0;--i)
if(f[a][i]!=f[b][i]){
ans=min(ans,min(val[a][i],val[b][i]));
a=f[a][i];
b=f[b][i];
}
return min(ans,min(val[a][0],val[b][0]));
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin>>n>>m; m<<=1;
for(int i=1;i<=m;i+=2){
ll u,v,w;
cin>>u>>v>>w;
a[i]=(edge){u,v,w};
a[i+1]=(edge){v,u,w};
}
for(int i=1;i<=n;++i) fa[i]=i;
for(int i=2;i<=n;++i) lg[i]=lg[i>>1]+1;
sort(a+1,a+m+1,cmp);
for(int i=1;i<=m;++i){
ll u=a[i].u,v=a[i].v,w=a[i].w;
ll x=find(u),y=find(v);
if(x!=y) fa[y]=x,add(u,v,w),add(v,u,w);
}
memset(val,63,sizeof(val));
for(int i=1;i<=n;++i){
if(vis[i]) continue;
vis[i]=1,dept[i]=1;
dfs_pre(i,0); //真是森林啊
}
cin>>q;
for(int i=1;i<=q;++i){
ll x,y;
cin>>x>>y;
if(find(x)!=find(y)){
cout<<"-1\n";
continue;
}
cout<<query_lca(x,y)<<'\n';
}
return 0;
}
ARC148D
智慧博弈论。首先如果每个数的出现次数都是偶数那么 Bob 珂以拿到和 Alice 一样的数,必赢。
从子问题入手,假设现在剩下两个数 \(a,b\),Bob 怎么样才会获胜。设 Alice 目前的和为 \(x\),Bob 的和为 \(y\),那么 Bob 一定会赢的充要条件为 \(x+a\equiv y+b(\:\mathtt{mod}\:\: M)\) 并且 \(x+b\equiv y+a(\:\mathtt{mod}\:\: M)\),将两个式子相减并移项可得 \(\mathbf{2}a\equiv\mathbf{2}b(\:\mathtt{mod}\:\: M)\),那么也就是只要降所有元素匹配起来就能让 Bob 获胜,反之 Alice 获胜。
注意到有 \(\mathbf{0}\le A_i\le M-\mathbf{1}\) 的限制,那么上面条件成立要么是 \(a=b\) 要么是 \(a\equiv b+\frac{m}{\mathbf{2}}(\:\mathtt{mod}\:\: M)\) 并且 \(M\) 为偶数。这样加上最开始的特判,如果模数为奇数那么 Alice 必赢。否则就直接用 set 来找这样的对数,先尽量匹配完 \(a=b\),然后因为每有一对满足 \(a\equiv b+\frac{m}{\mathbf{2}}(\:\mathtt{mod}\:\: M)\) 的数,两人之间的差都会增加 \(\frac{m}{\mathbf{2}}\),所以这样的对数要有偶数对 Bob 才能获胜,反之 Alice 获胜。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2*114514,M=1919810;
ll n,m,x;
set <ll> s;
map <ll,bool> ma;
int main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin>>n>>m;
for(int i=1;i<=2*n;++i){
cin>>x;
if(ma[x]) s.erase(x),ma[x]=0;
else s.insert(x),ma[x]=1;
}
if(!s.size()){
cout<<"Bob";
return 0;
}
if(m&1){
cout<<"Alice";
return 0;
}
for(ll i:s){
if(!ma[(i+m/2)%m]){ //m写成2还能过这么多点?
cout<<"Alice";
return 0;
}
}
x=s.size();
//注意你要把size/2,毕竟一对算了两次
if((x/2)&1) cout<<"Alice";
else cout<<"Bob";
return 0;
}
/*1 3
1 4*/
P2726 [SHOI2005] 树的双中心
先考虑一个 \(O(n^{\mathbf{2}})\) 的朴素做法:考虑枚举一条边将树划分成两部分,分别在两边找到 \(x,y\),找 \(x,y\) 用简单换根dp即可。正确性有,不想证。
考虑优化,珂以再想一个剪枝的贪心:我们发现如果以一个点子树内的点权总和 \(siz\) 为权值,那么一棵树的带权中心必定在根为开头的重链上。可以感性理解一下正确性,你走重儿子所增加的 \(siz\) 肯定是比走其它儿子小的。我们又发现这个题限制了树的深度 \(\le\mathbf{100}\),也就是说这个方法是完全可行的。
接下来是实现的过程和细节。我们珂以预处理出原树上每个点的 \(siz\) 和其它点到达它的总代价和 \(sum\),然后枚举断边,分别在两颗子树里走,一颗的根是 \(\mathbf{1}\),一颗是断边深度较大的点记为 \(v\)。我们要注意根为 \(\mathbf{1}\) 的子树是被截掉一部分的,所以我们要先让 \(\mathbf{1}\) 到 \(v\) 的链上的点的 \(siz\) 都减去 \(siz[v]\),并且一开始 \(dp_{\mathbf{1}}=sum_{\mathbf{1}}-sum_v-siz_v*dept_v\),然后正常转移。而且你的重儿子在减去了 \(siz[v]\) 之后就不一定是重儿子了,所以一开始我们还要记录每个点的次重儿子,在 dp 转移过程中比较哪个儿子更大。注意不要 dp 到另一棵子树去了。
复杂度 \(O(nh)\),代码有些冗余的地方可以优化。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=50005,M=1919810,inf=1e18;
struct xx{
ll next,to;
}e[2*N];
ll head[2*N],cnt;
void add(ll x,ll y){
e[++cnt].next=head[x];
e[cnt].to=y;
head[x]=cnt;
}
ll n,a[N],pa[N],pb[N];
ll dp[N],siz[N],dept[N],s1[N],s2[N];
ll f[N][32];
void dfs1(ll u,ll fa){
siz[u]=a[u];
for(int i=head[u];i;i=e[i].next){
ll v=e[i].to;
if(v==fa) continue;
dept[v]=dept[u]+1;
f[v][0]=u;
dfs1(v,u);
siz[u]+=siz[v];
if(siz[v]>=siz[s1[u]]) s2[u]=s1[u],s1[u]=v;
else if(siz[v]>=siz[s2[u]]) s2[u]=v;
}
}
ll sum[N],ans=inf;
void dfs2(ll u,ll fa){
for(int i=head[u];i;i=e[i].next){
ll v=e[i].to;
if(v==fa) continue;
dfs2(v,u);
sum[u]+=sum[v]+siz[v];
}
}
ll res,pos;
void dfs3(ll u,ll rt,ll id){
if(dp[u]<res) res=dp[u],pos=u;
if(!s1[u]||u==id) return;
ll v=s1[u];
dp[v]=dp[u]+(siz[rt]-siz[v])-siz[v];
dfs3(v,rt,id);
}
void dfs4(ll u,ll rt,ll id){
if(dp[u]<res) res=dp[u],pos=u;
ll v=s1[u];
if(v==id||siz[s2[u]]>siz[s1[u]]) v=s2[u];
if(!v) return;
dp[v]=dp[u]+(siz[rt]-siz[v])-siz[v];
dfs4(v,rt,id);
}
void solve(ll u,ll fa){
for(int i=head[u];i;i=e[i].next){
ll v=e[i].to;
if(v==fa) continue;
ll len=dept[v]-dept[1];
for(int now=u;now;now=f[now][0]) siz[now]-=siz[v];
dp[1]=sum[1]-sum[v]-siz[v]*len;
dp[v]=sum[v];
ll val=0;
res=inf,dfs3(v,v,u),val+=res;
res=inf,dfs4(1,1,v),val+=res;
ans=min(ans,val);
for(int now=u;now;now=f[now][0]) siz[now]+=siz[v];
solve(v,u);
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin>>n;
for(int i=1;i<n;++i){
ll a,b;
cin>>a>>b;
add(a,b),add(b,a);
}
for(int i=1;i<=n;++i) cin>>a[i];
dept[1]=1,dfs1(1,0);
dfs2(1,0);
solve(1,0);
cout<<ans;
return 0;
}//O(nh)
CF1753C
数学题。
考虑有效的操作次数有多少。我们的最终的目标是形如 \(\mathbf{0,0,0,\ldots,1,1,1}\) 这样的序列。设 \(cnt\mathbf{0},cnt\mathbf{1}\),那么珂以将目标转化为:将前 \(cnt\mathbf{0}\) 个数中的 \(\mathbf{1}\) 和后 \(cnt\mathbf{1}\) 个数中的 \(\mathbf{0}\) 交换,我们令这样的交换次数为 \(x\),那么每步操作有效的概率是 \(\dfrac{x^{\mathbf{2}}}{n\times(n-\mathbf{1})/\mathbf{2}}\),期望是概率的倒数,所以每一步的答案就是 \(\dfrac{n\times(n+\mathbf{1})/\mathbf{2}}{i^{\mathbf{2}}}\),要取模就乘个逆元,注意循环变量 \(i\) 要开 long long。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2*114514,M=1919810,mod=998244353;
ll qpow(ll a,ll b){
ll ans=1;
while(b){
if(b&1) ans=ans*a%mod;
a=a*a%mod;
b>>=1;
}
return ans;
}
ll T;
ll n,a[N];
ll sum,ans;
void solve(){
cin>>n; sum=n*(n-1)/2,sum%=mod;
ll cnt0=0,cnt1=0; ans=0;
for(int i=1;i<=n;++i) cin>>a[i],cnt0+=(a[i]==0);
for(int i=1;i<=cnt0;++i) cnt1+=a[i];
for(ll i=cnt1;i>=1;--i) ans=(ans+sum*qpow(i*i,mod-2ll)%mod)%mod;
cout<<ans<<'\n';//
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin>>T;
while(T--) solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号