线性结构和非线性结构、稀疏数组、队列、链表(LinkedList)
一、线性结构和非线性结构
线性结构:
1)线性绪构作为最常用的数据结构,其特点是数据元素之间存在一对一的线性关系
2)线性结构有两种不同的存储结构,即顺序存储结构和链式存储结构。顺序存储的
线性表称为顺序表,顺序表中的存储元素是连续的
3)链式存储的线性表称为链表,链表中的存储元素不一定是连续的,元素节点中存
放数据元素以及相邻元素的地址信息
4)线性结构常见的有:数组、队列、链表和栈,后面我们会详细讲解.
非线性结构:
非线性结构包括:二维数组,多维数组,广义表,树结构,图结构
二、稀疏数组
基本介绍:当一个数组中大部分元素为0,或者为同一个值的数组时,可以使用稀疏数组来保存该数组。
稀疏数组的处理方法是:
1)记录数组一共有几行几列,有多少个不同的值
2)把具有不同值的元素的行列及值记录在一个小规模的数组中,从而缩小程序的规模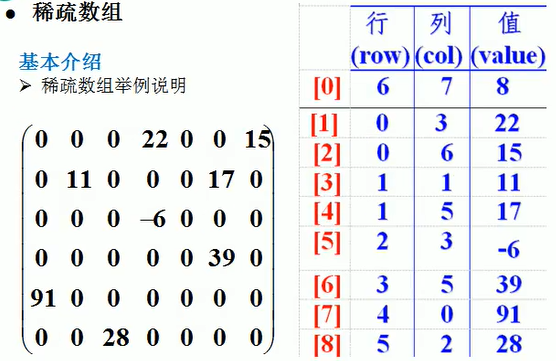

//实现原始数组和稀疏数组的相互转换;并存入文件进行保存和读取 package com.zjl.sparsearray; import java.io.*; public class SparseArray { public static void main(String[] args) throws IOException { String file = "C:\\Users\\wenman\\Desktop\\test\\sapraseArr.txt"; //定义一个原始的数组arr[11][11],并赋值arr[1][2] = 1, arr[2][3] = 2 int[][] arr = new int[11][11]; arr[1][2] = 1; arr[2][3] = 2; arr[3][4] = 2; //查看原始数据 for (int[] arr_:arr) { for (int num:arr_) { System.out.printf("%d ",num); } System.out.println(); } //获取原始数据中的数据个数 int nums = 0; for (int[] arr_:arr) { for (int num:arr_) { if (num != 0){ nums++; } } } //将原始数组转变为稀疏数组 int[][] sparseArr = new int[nums + 1][3]; sparseArr[0][0] = 11; sparseArr[0][1] = 11; sparseArr[0][2] = nums; int count = 0; for (int i = 0; i < 11; i++) { for (int j = 0; j < 11; j++) { if (arr[i][j] != 0){ count++; sparseArr[count][0] = i; sparseArr[count][1] = j; sparseArr[count][2] = arr[i][j]; } } } /** * 将稀疏数组存入到文件中 */ FileWriter fileWriter = new FileWriter(file); for (int i = 0;i<sparseArr.length;i++) { fileWriter.write(sparseArr[i][0]+" "+sparseArr[i][1]+" "+sparseArr[i][2]+"\n"); } fileWriter.close(); //输出稀疏数组结构 for (int[] arr_:sparseArr) { for (int num:arr_ ) { System.out.printf("%d ",num); } System.out.println(); } /** * 从文件中读取数组 */ BufferedReader bufferedReader = new BufferedReader(new FileReader(file)); String line = null; int lineNum = 0; //初始化原始数组 String[] s = bufferedReader.readLine().split(" "); int[][] arrs = new int[Integer.parseInt(s[0])][Integer.parseInt(s[1])]; //获取原始数组中的值并赋值 while ((line = bufferedReader.readLine())!=null) { String[] s1 = line.split(" "); arrs[Integer.parseInt(s1[0])][Integer.parseInt(s1[1])] = Integer.parseInt(s1[2]); } bufferedReader.close(); //将稀疏数组变成原始数组 // int[][] arrs = new int[sparseArr[0][0]][sparseArr[0][1]]; // for (int i = 1 ; i < sparseArr.length; i ++) { // arrs[sparseArr[i][0]][sparseArr[i][1]] = sparseArr[i][2]; // } for (int[] arr_:arrs) { for (int num:arr_) { System.out.printf("%d ",num); } System.out.println(); } } }
三、队列
介绍:
1、队列是一个有序列表,可以用数组或者链表来实现,
2、遵循先入先出的原则。即:先存入队列的数据,要先取出。后存入的要后取出
用数组模拟:
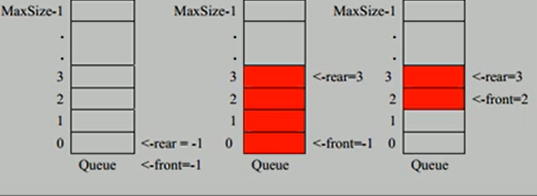
在入队和出队时:
因为队列的输出、输入是分别从前后端来处理,因此需要两个变量front及rear分别记录队列前后端的下标,front会随着数据输出而改变(变大),而rear则是随着数据输入而改变(变大)尾进头出,先进先出
三、单链表链表(Linked List)
介绍:链表是有序的列表
1)链表是以节点的方式来存储
2)每个节点包括data域(数据域)和next域(指向下一个节点)
3)链表的各个节点不一定是连续的
4)链表分带头节点的链表和没有头结点的链表,根据实际的需求来确定
单链表存储结构示意图:(内存)

单链表(带头结点)逻辑结构示意图
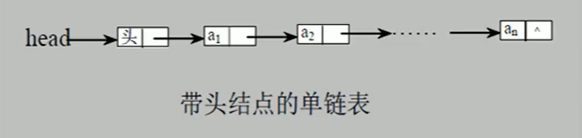
单链表的常见面试题:

//node结点 public class HeroNode { public int no; public String name; public HeroNode next; public HeroNode(int no, String name) { this.no = no; this.name = name; } @Override public String toString() { return "no=" + no + ", name=" + name ; } } //单链表相关函数 import jdk.nashorn.internal.objects.annotations.Where; import java.util.Stack; public class HeroLinkedList { private HeroNode head = new HeroNode(0,""); public HeroNode getHead() { return head; } //添加或者修改存在的节点 public void addOrUPdateNode(HeroNode node){ if (node == null) { System.out.println("加入失败,不能加入空对象"); } HeroNode temp = head; while (true){ if (temp.next == null) { temp.next = node; break; } if (temp.next.no == node.no) { temp.next.name = node.name; break; } if ( temp.next.no > node.no && temp.no < node.no ) { node.next = temp.next; temp.next = node; break; } temp = temp.next; } } //删除某个节点 public void deleteNode(int i){ HeroNode temp = head; while (temp.next != null) { if (temp.next.no == i) { temp.next = temp.next.next; return; } temp = temp.next; } System.out.println("删除失败,没有这个节点!"); } //展示所有的节点 public void allNode(){ HeroNode temp = head; while (temp.next != null) { System.out.println(temp.next); temp = temp.next; } } //返回节点的所有个数 public int nodeSum(HeroNode head){ if (head == null || head.next == null) { return 0; } int num = 0; HeroNode temp = head; while (temp.next != null) { temp = temp.next; num++; } return num; } //查找单链表的倒数第N个节点 public void findHeroNode(HeroNode head,int n){ if (n <= 0 || n > nodeSum(head)) { System.out.println("单链表中没有这个节点!"); return; } int m = nodeSum(head)-n; HeroNode temp = head; while (m>0){ temp = temp.next; m--; } System.out.println(temp.next); } //反转单向链表并输出 public void reverseHeroNode(){ //定义一个新的头结点 HeroNode reNode = new HeroNode(0,""); boolean exange = false; HeroNode tempHead = null; if (head.next != null) { tempHead = head.next; } HeroNode temp; while (tempHead != null) { temp = tempHead; tempHead = tempHead.next; temp.next = reNode.next; reNode.next = temp; exange = true; } if (exange){ head = reNode; } } //逆序打印单向链表 public void reversePrint(){ if (head == null) { return; } //使用栈,先进后出的顺序,按正常顺序存入栈中,出栈时就是逆序 Stack<HeroNode> hero = new Stack<>(); HeroNode temp = head; while (temp.next != null) { hero.add(temp.next); temp = temp.next; } while (!hero.isEmpty()) { System.out.println(hero.pop()); } } //合并两条单链表,使得排序之后仍然有序 public void mergesLinkedList(HeroLinkedList list){ if (list == null){ return; } if (list.head.next == null){ return; } HeroNode temp = list.head.next; HeroNode tempAdd = null; while (temp != null){ tempAdd = temp; temp = temp.next; this.addOrUPdateNode(tempAdd); } } } //测试单链表相关方法 package com.zjl.linked_list; public class testLinkedList { public static void main(String[] args) { HeroNode node1 = new HeroNode(1, "张三"); HeroNode node5 = new HeroNode(5, "二麻子"); HeroNode node6 = new HeroNode(6, "王五"); HeroNode node2 = new HeroNode(2, "李四"); HeroNode node3 = new HeroNode(3, "大头"); HeroNode node4 = new HeroNode(4, "小鬼"); // HeroNode node31 = new HeroNode(3, "王五$$"); HeroLinkedList list = new HeroLinkedList(); HeroLinkedList list1 = new HeroLinkedList(); //添加节点 list.addOrUPdateNode(node1); list.addOrUPdateNode(node2); list.addOrUPdateNode(node5); list.addOrUPdateNode(node6); list1.addOrUPdateNode(node3); list1.addOrUPdateNode(node4); //展示所有节点 list.allNode(); list1.allNode(); //删除某个节点 // list.deleteNode(3); // list.allNode(); //要删除的节点不存在时 // list.deleteNode(3); // list.deleteNode(5); //获取节点的总个数 System.out.println(list.nodeSum(list.getHead())); //找到单向链表的倒数第n个数 // list.findHeroNode(list.getHead(),1); //反转单链表 // list.reverseHeroNode(); // list.allNode(); //逆序输出单向链表 // list.reversePrint(); //合并两个单链表,并且合并之后依然有顺序 list.mergesLinkedList(list1); list.allNode(); } }
二、双向链表
特点:
1、具有next指向下一个指针,也有per指向上一个指针
2、查找方式,可以向前也可以向后
3、可以自我删除

单向链表和双向链表的不同:

//双向链表结点的定义 public class HeroNode { public int no; public String name; public HeroNode next; public HeroNode per; public HeroNode(int no, String name) { this.no = no; this.name = name; } @Override public String toString() { return "no=" + no + ", name=" + name ; } } //双向链表相关的方法 import com.zjl.linked_list.HeroNode; import jdk.nashorn.internal.objects.annotations.Where; public class HeroDoubleLinkedList { HeroNode head = new HeroNode(0, ""); //双向链表的添加和更改 public void addDoubleLinkedList(HeroNode node){ if (node == null){ return; } HeroNode temp = head; while (true) { if (temp.next == null){ temp.next = node; node.per = temp; break; } if (temp.next.no == node.no) { temp.next.name=node.name; break; } if ( temp.no < node.no && temp.next.no > node.no) { node.next = temp.next; temp.next.per = node; temp.next = node; node.per = temp; break; } temp = temp.next; } } //展示所有的双向链表 public void allDoubleLinkedList(){ if (head == null) { return; } HeroNode temp = head; while (temp.next != null) { System.out.println(temp.next); temp = temp.next; } } //删除双向链表的节点 public void deleteDoubleLinkedliseNode(int node){ if (head == null && node > 0) { return; } boolean loop = true; HeroNode temp = head; while (temp != null) { if (temp.no == node) { temp.next.per = temp.per; temp.per.next = temp.next; loop = false; break; } if (loop) { temp = temp.next; } } System.out.println("双向链表中,没有这个结点!"); } } //测试双向链表; import com.sun.org.apache.bcel.internal.generic.NEW; import com.zjl.linked_list.HeroNode; public class testDoubleLinkedList { public static void main(String[] args) { HeroDoubleLinkedList list = new HeroDoubleLinkedList(); HeroNode node1 = new HeroNode(1, "张三"); HeroNode node2 = new HeroNode(2, "李四"); HeroNode node3 = new HeroNode(3, "二麻子"); HeroNode node4 = new HeroNode(4, "王五"); //添加结点到双向链表中 list.addDoubleLinkedList(node1); list.addDoubleLinkedList(node2); list.addDoubleLinkedList(node3); list.addDoubleLinkedList(node4); //展示双向链表中的所有节点 list.allDoubleLinkedList(); //删除双向链表中的一个结点 list.deleteDoubleLinkedliseNode(2); list.allDoubleLinkedList(); } }
三、单向环形链表
约瑟夫问题:

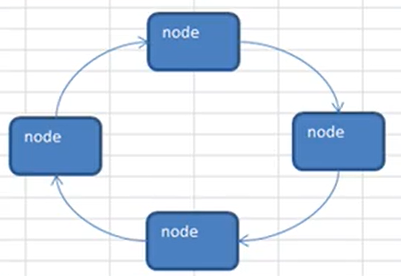
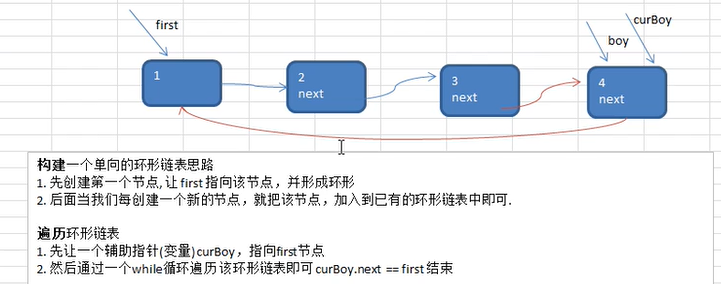
约瑟夫问题的解决思路,用一个头指针表示当前到达的位置,用一个辅助指针表示当前位置的前一个位置(方便进行删除操作),当first移动到要出圈的位置,就进行出圈操作,当已经到达first和辅助指针指向同一个位置时,就表示环形链表中自剩下一个结点,结束出圈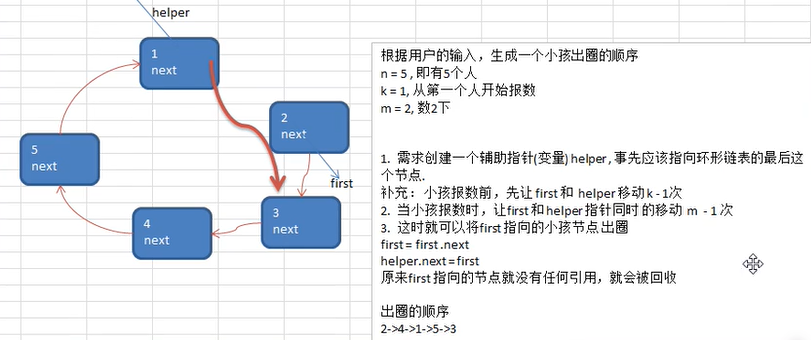
完成一个关于约瑟夫问题的求解:
//定义将用到的结点 package com.zjl.josepfu; public class Child { public int no; public Child next; public Child(int no) { this.no = no; } public int getNo() { return no; } @Override public String toString() { return "Child=" + no; } } //定义在环形链表中,解决约瑟夫问题的方法 package com.zjl.josepfu; public class Josepfu { public Child first = new Child(-1); //添加环形链表 public void addNewChild(int nums){ if (nums < 1) { System.out.println("输入的数量不合适!"); } Child temp = first; Child boy = first; if (nums == 1) { boy.next = new Child(1); boy = boy.next; boy.next = temp.next; } else{ for (int i = 1; i <= nums; i++) { boy.next = new Child(i); boy = boy.next; boy.next = temp.next; } } } //输出环形链表中的所有结点 public void allJosepfu(){ if (first.next == null) { System.out.println("该环没有结点"); return; } Child temp = first.next; Child boy = first.next; while (true) { System.out.println(boy); boy = boy.next; if (boy == temp) { break; } } } //删除环中的某一个节点 public void deleteJosepfyNode(Child node){ if (node == null) { System.out.println("删除的节点不能为空!"); } if (first.next == null) { System.out.println("该环形链表为空"); } Child temp = first.next; Child boy = first.next; while (true) { if (temp.no == node.no) { first.next = temp.next; } if (boy.no == boy.next.no && boy.next.no == node.no) { first.next = null; break; } if (boy.next.no == node.no ) { boy.next = boy.next.next; break; } boy = boy.next; } } //获取环形链表的节点个数 public int allJosepfuNum(){ if (first.next == null) { System.out.println("该环没有结点"); return 0; } int num = 0; Child temp = first.next; Child boy = first.next; while (true) { // System.out.println(boy); boy = boy.next; num++; if (boy == temp) { break; } } return num; } //进行约瑟夫环的操作,根据输入的确定的起点和间隔,在已知的环形链表进行约瑟夫问题求解 public void testJosepfu(int k,int m){ if (k > allJosepfuNum() || k <= 0) { System.out.println("该环中没有该起点!"); return; } Child boy = first;//找到头结点,开始一个环链表 //找到环形链表中的对应的起点k值 while (boy.next.no != k) { boy = boy.next; } //循环的次数 int m_temp = m; while (true) { boy = boy.next; m_temp--; //每向下找一个结点就将间隔距离减一 //当距离变为0时找到对应的值输出,并从环链表中删除该值,并重新设置距离 if (m_temp == 0) { System.out.println(boy); deleteJosepfyNode(boy); m_temp = m; } //当环形链表中只剩下一个结点的时候,就输出该结点并退出循环 if (allJosepfuNum() == 1) { allJosepfu(); break; } } } //直接对约瑟夫问题进行求解,可以直接确定环的长度,起点,和间隔的距离 public void testJosepfu(int k, int m, int num) { if (k < 1 || k > num) { System.out.println("输入的参数有问题!"); } addNewChild(num); Child helper = first.next; while (helper.next != first.next) { helper = helper.next; } first = first.next; while (first.no != k){ first = first.next; helper = helper.next; } int temp = m-1; while (true){ first = first.next; helper = helper.next; temp--; if (helper == first){ allJosepfu(); break; } if (temp == 0) { System.out.println(first); first = first.next; helper.next = first; temp = m-1; } } } } //测试方法 package com.zjl.josepfu; public class TestJosepfu { public static void main(String[] args) { Josepfu josepfu = new Josepfu(); Josepfu josepfu1 = new Josepfu(); //给约瑟夫环加入结点 josepfu.addNewChild(5); // System.out.println(josepfu.allJosepfuNum()); // //输出所有的结点 // josepfu.allJosepfu(); // josepfu.deleteJosepfyNode(new Child(3)); // josepfu.allJosepfu(); // System.out.println(josepfu.allJosepfuNum()); //测试进行约瑟夫实验 josepfu.testJosepfu(1,2); // josepfu.allJosepfu(); //输入起点,间隔,以及环形链表的大小,进行约瑟夫问题的解决 josepfu1.testJosepfu(1,2,5); } }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号