hdoj 1030 Delta-wave

Problem Description
A triangle field is numbered with successive integers in the way shown on the picture below.



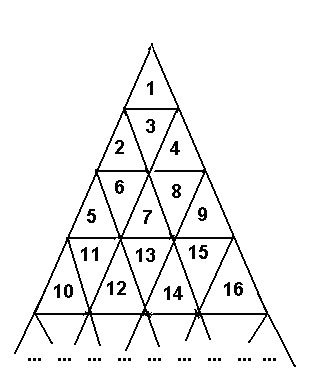
The traveller needs to go from the cell with number M to the cell with number N. The traveller is able to enter the cell through cell edges only, he can not travel from cell to cell through vertices. The number of edges the traveller passes makes the length of the traveller's route.

Write the program to determine the length of the shortest route connecting cells with numbers N and M.
 

 

Input
Input contains two integer numbers M and N in the range from 1 to 1000000000 separated with space(s).
 

 

Output
Output should contain the length of the shortest route.
 

 

Sample Input
6 12
 

 

Sample Output
3
 1 /*numlay为格子所在的层数 则nunlay*numlay就是该行最后一个数字
 2 两行的最后一格的数相减就是下一行的个数  计算出左边界
 3 再加两倍的行差就是右边界了！而且正三角所到的边界是正三角型，反三角所到的边界是反三角型，这点要注意！
 4  */
 5 #include <stdio.h>
 6 #include<math.h>
 7  int main()
 8 {
 9     int temp,n,m,s,flag=3,nlay,mlay,zb,yb,cc,k,sj;
10     while(scanf("%d%d",&m,&n)==2 )
11     { 
12         flag=3;s=0;k=0;
13         if(m>n)   { temp=m;m=n; n=temp;}
14         nlay=(int)ceil(sqrt(n));//判断n和m所在层数
15          mlay=(int)ceil(sqrt(m));
16         cc=abs(nlay-mlay);//判断两点层差
17          zb=m+(nlay-1)*(nlay-1)-(mlay-1)*(mlay-1);//判断m辐射到n层所及范围的左边界和右边界
18          yb=zb+2*cc;
19 
20         if(n>=zb && n <=yb) //判断n在m范围所须步数
21          {
22             s=2*(cc);k=1;}
23             else
24             {      
25                 if(n<zb) //判断n到m边界及m点所须步数和
26                   s=2*(cc)+abs(n-zb); 
27                 else
28                   s=2*(cc)+abs(n-yb);
29             }
30             sj=m-(mlay-1)*(mlay-1);//判断三角类型0正,1倒
31             if(abs(n-m)% 2 !=(cc) % 2)
32             {
33                 if(sj % 2 ==1 )
34                     flag=1;
35                 else
36                     flag=0;
37             }
38          if(flag==1 && k==1) s=s-1;//假如n点在m点辐射范围内,正三角-1,倒三角+1,不在不判断.
39          if(flag==0 && k==1) s=s+1;
40          printf("%d\n",s);
41     }return 0;
42 }
43 
44 




 
posted @ 2010-05-09 16:58  にんじゃ  阅读(516)  评论(0)    收藏  举报