实现迪杰斯特拉算法
如下图,使用迪杰斯特拉算法求下图的最短路径
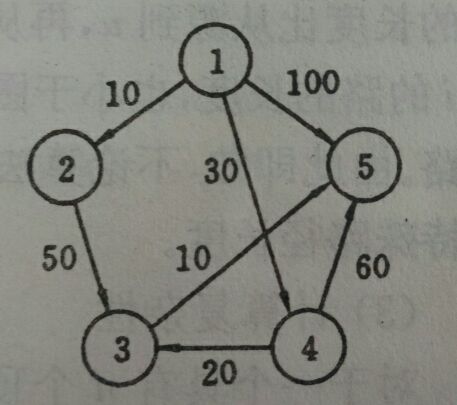
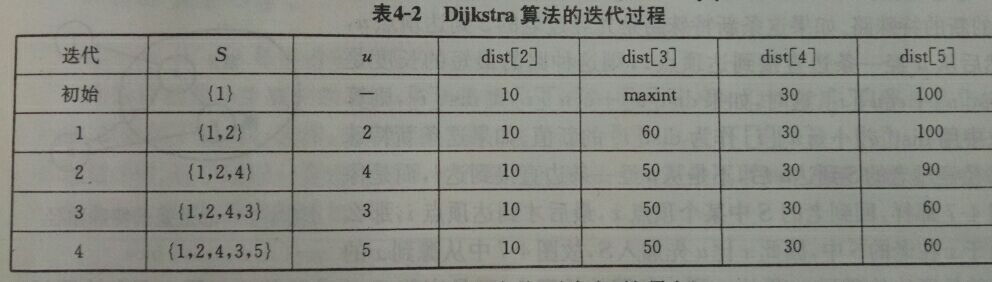
跌代过程:
1) 初始时从1开始寻找各节点到该节点的距离,路不通设置为maxint,此时把1归为s里面
2)从1)得到距离1最短的路径对应的结点如上图为2,并把2归到s里面并求各节点(剩下的不在s里面的)到2的距离,如果新的距离更小的话则更新dist[i]
3) 从2)得到距离2最短的路径对应的结点如上图为4,并把4归到s里面并求各节点(剩下的不在s里面的)到4的距离,如果新的距离更小的话则更新dist[i]
4)依次类推可以把算有的节点遍历,并且最终的dist[i]便是从初始节点1到i的最短路径
算法如下
1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 int main() 6 { 7 cout << "请输入图的顶点数" << endl; 8 int n; 9 cin >> n; 10 int Amap[n+1][n+1]; 11 for(int i=1;i<=n;i++){//初始化map 12 for(int j=1;j<=n;j++){ 13 Amap[i][j]=99999; 14 } 15 } 16 cout << " 请输入图的边数" << endl; 17 int m; 18 cin >> m; 19 cout << " 请输入图的边的起点和终点和边的长度" << endl; 20 int t1=0; 21 int t2=0; 22 int t3=0; 23 for(int j=0;j<m;j++){//更改t1到t2的长度 24 cin >> t1 >> t2 >> t3; 25 Amap[t1][t2]=t3; 26 } 27 int foot[n+1];//记录顶点是否归到已确定的路径里面 28 memset(foot,0,sizeof(foot)); 29 foot[1]=1;//默认从1开始 30 int dist[n+1];//记录每个顶点所对应的最短特殊路径 31 for(int i=1;i<=n;i++){ 32 dist[i]=Amap[1][i];//初始化第一个顶点的dist数组 33 } 34 int as[n];//用来记录经过的顶点顺序 35 memset(as,0,sizeof(as)); 36 as[0]=1;//默认从一开始 37 int u; 38 for(int i=1;i<=n-1;i++){ 39 int min=99999; 40 for(int j=1;j<=n;j++){//获取到该顶点的最短路径对应的下一个顶点的位置u 41 if(foot[j]==0 && dist[j]< min){ 42 min=dist[j]; 43 u=j; 44 } 45 } 46 foot[u]=1;//设置为一,表示已经选取 47 as[i]=u;//记录下来该顶点 48 for(int k=1;k<=n;k++){//更新当前的dist数组 49 if(Amap[u][k]<99999){//表示顶点之间有路径 50 if(dist[k]>dist[u]+Amap[u][k]){//当前该顶点的dist不是最短的则更新 51 dist[k] =dist[u] + Amap[u][k]; 52 } 53 } 54 } 55 56 } 57 cout << " 最短路径经过的顶点为"<<endl; 58 for(int i=0;i<n;i++){ 59 cout << as[i] << " "; 60 } 61 cout << endl; 62 cout << "从一到各个顶点的长度为" << endl; 63 for(int i=1;i<=n;i++){ 64 if(dist[i]==99999){ 65 cout <<"从1到"<<i<< "的长度为"<<"-" << endl; 66 continue; 67 } 68 cout <<"从1到"<<i<< "的长度为"<<dist[i] << endl; 69 } 70 return 0; 71 }
运行结果截图为
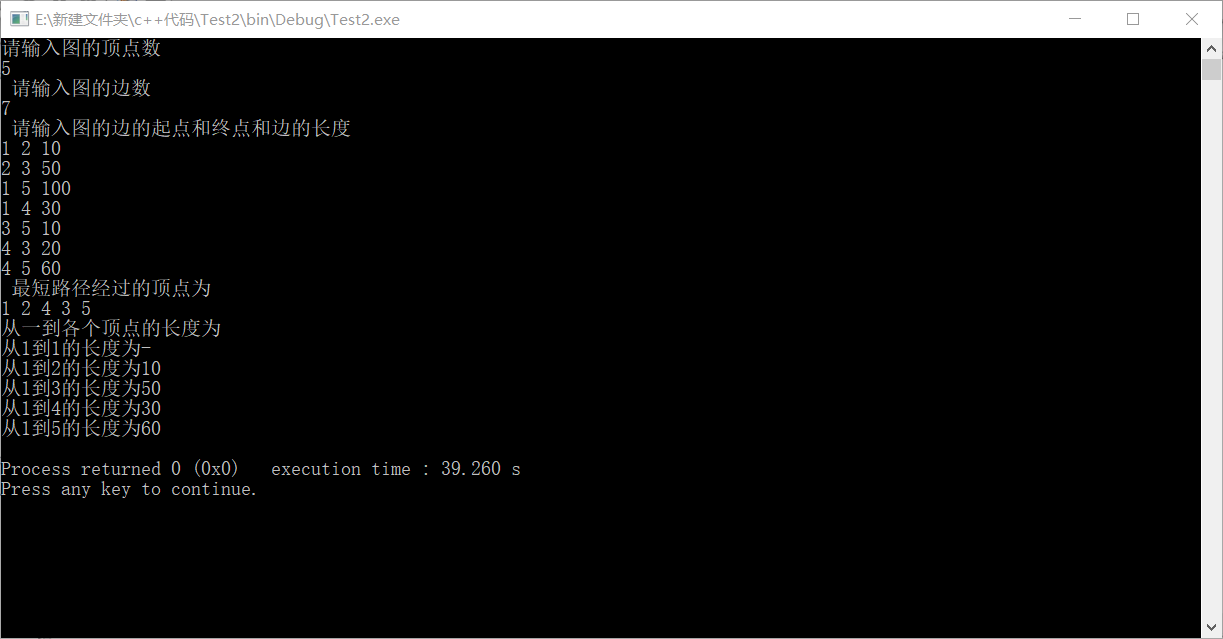
上述的代码并没有把从1到其它点的具体路径记录下来,下面是对上面的代码的升级,实现了路径的记录。
1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 int main() 6 { 7 //freopen("D:/Data1.txt","r",stdin); 8 cout << "请输入图的顶点数" << endl; 9 int n; 10 cin >> n; 11 int road[n+1][n+1][n+1];//用来记录路径; 12 memset(road,0,sizeof(road)); 13 14 int Amap[n+1][n+1]; 15 for(int i=1;i<=n;i++){//初始化map 16 for(int j=1;j<=n;j++){ 17 Amap[i][j]=99999; 18 } 19 } 20 cout << " 请输入图的边数" << endl; 21 int m; 22 cin >> m; 23 cout << " 请输入图的边的起点和终点和边的长度" << endl; 24 int t1=0; 25 int t2=0; 26 int t3=0; 27 for(int j=0;j<m;j++){//更改t1到t2的长度 28 cin >> t1 >> t2 >> t3; 29 Amap[t1][t2]=t3; 30 } 31 for(int i=1;i<=1;i++){//初始化路线 32 for(int j=1;j<=n;j++){ 33 for(int k=1;k<=2;k++){ 34 if(k==1){ 35 road[i][j][k]=1; 36 } 37 if(Amap[i][j]!=99999&&k==2){ 38 road[i][j][k]=j; 39 } 40 } 41 } 42 } 43 int foot[n+1];//记录顶点是否归到已确定的路径里面 44 memset(foot,0,sizeof(foot)); 45 foot[1]=1;//默认从1开始 46 int dist[n+1];//记录每个顶点所对应的最短特殊路径 47 for(int i=1;i<=n;i++){ 48 dist[i]=Amap[1][i];//初始化第一个顶点的dist数组 49 } 50 int as[n];//用来记录经过的顶点顺序 51 memset(as,0,sizeof(as)); 52 as[0]=1;//默认从一开始 53 int u; 54 for(int i=1;i<=n-1;i++){ 55 int min=99999; 56 for(int j=1;j<=n;j++){//获取到该顶点的最短路径对应的下一个顶点的位置u 57 if(foot[j]==0 && dist[j]< min){ 58 min=dist[j]; 59 u=j; 60 } 61 } 62 foot[u]=1;//设置为一,表示已经选取 63 as[i]=u;//记录下来该顶点 64 for(int k=1;k<=n;k++){//更新当前的dist数组 65 if(Amap[u][k]<99999&&foot[k]==0){//表示顶点之间有路径 66 if(dist[k]>dist[u]+Amap[u][k]){//当前该顶点的dist不是最短的则更新 67 dist[k] =dist[u] + Amap[u][k]; 68 for(int i1=1;i1<=n;i1++){//新的路径比原来的路径更短时更新并记录这个新的路径 69 if(road[1][u][i1]!=0){ 70 road[1][k][i1]=road[1][u][i1]; 71 } 72 else{ 73 road[1][k][i1]=k; 74 break; 75 } 76 } 77 } 78 } 79 } 80 81 } 82 cout << " 最短路径经过的顶点为"<<endl; 83 for(int i=0;i<n;i++){ 84 cout << as[i] << " "; 85 } 86 cout << endl; 87 cout << "从一到各个顶点的长度为" << endl; 88 for(int i=1;i<=n;i++){ 89 if(dist[i]==99999){ 90 cout <<"从1到"<<i<< "的长度为"<<"-" << endl; 91 continue; 92 } 93 cout <<"从1到"<<i<< "的长度为"<<dist[i] << endl; 94 cout <<"从1到"<<i<< "的路径为:"; 95 for(int i1=1;i1<=n;i1++){ 96 if(road[1][i][i1]!=0){ 97 cout << road[1][i][i1] <<"-->"; 98 } 99 } 100 cout << "end" << endl; 101 } 102 return 0; 103 }
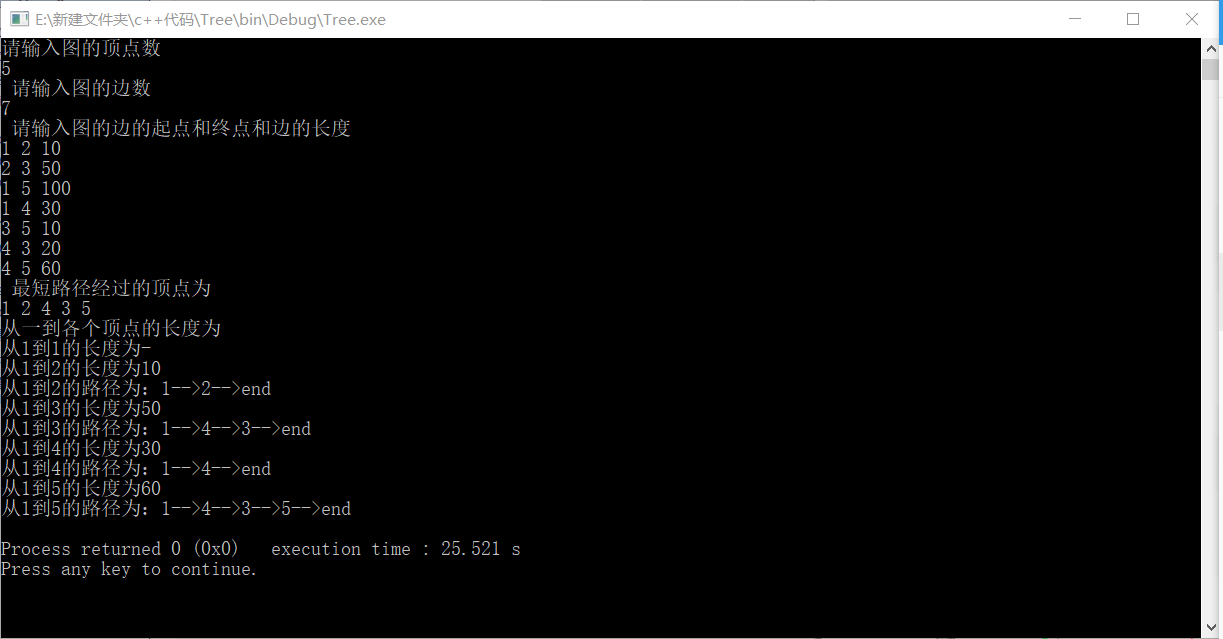
作者:你的雷哥
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须在文章页面给出原文连接,否则保留追究法律责任的权利。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号