【区块链与隐私保护从入门到精通系列教程】第x篇 隐私保护概述

1. 面向隐私保护的机器学习

Privacy-Preserving Machine Learning，PPML系统：使用了保护用户隐私和数据安全的防御技术的机器学习。

信息安全：本质上指控制访问和处理信息的权力。

对于PPML的一些著名方法有：安全多方计算（MPC）、供隐私保护模型训练和预测使用的同态加密方法（HE）、防止数据泄漏的差分隐私（DP）方法。

 

关于安全机器学习（secure ML）和PPML的区别：

 

 

 注：

1、机器学习系统的特性：

机密性：对机密性的攻击可能导致一些机器学习的敏感信息（如训练数据或训练模型）会出现泄漏；

完整性：对完整性的攻击可能导致机器学习系统出现检测错误、如可能将入侵点检测为正常（假阴性）。

可用性：对可用性的攻击可能导致系统出现分类错误（假阴性和假阳性），系统变为不可用的。

 

2. 隐私保护技术

2.1 安全多方计算

安全多方计算是从安全两方计算问题引出的，即“百万富翁问题”。

百万富翁问题：

百万富翁问题是姚期智先生在1982年提出的第一个安全双方计算问题。

问题可以描述为：两个百万富翁街头邂逅，他们都想炫一下富，比比谁更有钱，但是出于隐私，都不想让对方知道自己到底拥有多少财富，如何在不借助第三方的情况下，让他们知道他们之间谁更有钱。

关于百万富翁问题，数学原理可以参考这篇博客：

https://blog.csdn.net/qq_45764888/article/details/126076430

定义：安全多方计算协议能够实现互相不信任的人在无可信方的情况下共同完成某个计算目标，同时又不泄漏各自的隐私输入。

安全多方计算允许我们计算私有输入值的函数，从而使每一方只能得到其相应的函数输出值，而不能得到其他方的输入值与输出值。

安全多方计算能够通过三种不同的框架来实现：不经意传输（OT）、秘密共享（SS）、阈值同态加密（THE）。

2.1.1 不经意传输

不经意传输是Rabin在1981年提出的两方计算协议。

在不经意传输中，发送方拥有一个“消息-索引”对（M1，1），（Mn, n)。在每次传输时，接收方选择一个索引i，并接收Mi。接收方不能得知关于数据库的任何其他信息，发送方也不能了解关于接收方i选择的任何信息。

n取1的不经意传输：设A方有一个输入表（x1, ...xn)作为输入，B方有i属于1, ...n作为输入。n取1的不经意传输是一种安全多方计算协议，其中A不能学习到关于i的信息，B只能学习到xi。

2.1.2 秘密共享

秘密共享的思想是将秘密以适当的方式拆分，拆分后的每一个份额由不同的参与者管理，只有若干个参与者一同协作才能恢复秘密消息。

这里有两点：

（1）单个参与者无法恢复秘密信息；

（2）当其中任何相应范围内参与者出问题时，秘密仍可以完整恢复。

秘密共享的目的是阻止秘密过于集中，秘密共享能有效地防止系统外敌人的攻击和系统内用户的背叛。

2.2 同态加密

同态加密的定义：对经过同态加密的数据进行处理得到一个输出，将这一输出进行解密，其结果与用同一方法处理未加密的原始数据得到的输出结果是一样的。

对于同态加密领域，对称加密和非对称加密界限不是很明确了，因为我们对密钥的要求是相同的。

同态加密技术包含密钥生成算法、加密算法、解密算法、评估算法。

分类：

1、根据对于数据处理的运算符不同来分类：

1）加法同态：

2）乘法同态：

3）全同态：

2、根据运算次数要求来分类：

1）部分同态：

2）些许同态：

3）全同态：略，同上。

具体公式如下：

 

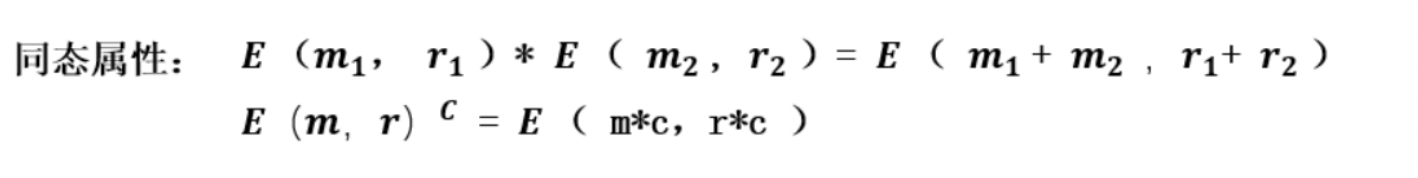
2.3 差分隐私

当敌手试图从数据库中查询个体信息时将其混淆，使得敌手无法从查询结果中辨别个体级别的敏感性。

差分隐私主要通过给数据加上噪声实现，有两种方法：

1）根据函数的敏感性增加噪声；

2）根据离散值的指数分布选择噪声。