「csp模拟」模拟测试3

- 报零很难受, T1 的话,暴力可以拿到30分,我却因为一些小错误恶心的报零了。
- T2 当时是真的没有想到怎么dp,但是考后看看发现dp并不难想,虽然当时不会非质数取mod,但还是有30分的暴力的。
- 最恶心的是 T3,直接模拟,我几乎全场都在做这道题,但是,到了最后上交时,发现自己的题意理解错了,并没有看错题意,只是在打着打着题意就记混了,方向判错了,以为 \(\text{(1, 1)}\) 是坐标上的 \(\text{(1, 1)}\),于是就向右上方向跑了!!!这种问题应该避免,想清楚所有后再打,打的时候回想题意,不要打着打着题意就变了味道。
回家


题解
- 圆方树
- 问题就是 \(1\) 到 \(n\) 路径上的割点个数。
- \(\text{tarjan}\) 缩点双,建出圆方树来,然后 \(\text{DFS}\) 一遍求出来就好了
code
#include <bits/stdc++.h>
using namespace std;
#define cle(a) memset(a, 0, sizeof(a));
#define print(x) cerr << #x << " : " << x << endl;
inline int read() {
int k = 0, f = 1; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if(ch == '-') f = -1;
for (; isdigit(ch); ch = getchar()) k = k * 10 + ch - '0' ;
return k * f;
}
const int maxn = 480000 + 100;
int low[maxn], dfn[maxn], dfs_clock, cut[maxn], top, root, sta[maxn];
vector <int> e[maxn], g[maxn], ans;
int num, tot;
void Tarjan(int u){
dfn[u]=low[u]=++dfs_clock;
sta[++top]=u;
int flag=0;
for(auto v : g[u]){
if(!dfn[v]){
Tarjan(v);
low[u]=min(low[u],low[v]);
if(dfn[u]<=low[v]){
flag++;
if(u!=root||flag>1)cut[u]=1;
}
if(dfn[u]==low[v]){
tot++;
while(1){
int x=sta[top--];
e[tot].push_back(x);
e[x].push_back(tot);
if(x==v)break;
}
e[u].push_back(tot);
e[tot].push_back(u);
}
}else low[u]=min(low[u],dfn[v]);
}
}
void tarjan(int u) {
low[u] = dfn[u] = ++ dfs_clock;
sta[++top] = u;
for (auto v : g[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
if (dfn[u] <= low[v]){
num ++;
if(u != root || num > 1) cut[u] = 1;
}
if (low[v] == dfn[u]) {
tot++;
while(1){
int x = sta[top--];
e[tot].push_back(x);
e[x].push_back(tot);
if(x == v)break;
}
e[tot].push_back(u);
e[u].push_back(tot);
}
} else low[u] = min(low[u], dfn[v]);
}
}
int fa[maxn], depth[maxn];
void dfs(int u, int f = 1) {
for (auto v : e[u]) {
if (v == f) continue;
fa[v] = u;
depth[v] = depth[u] + 1;
dfs(v, u);
}
}
int main() {
#ifdef local
freopen("in","r",stdin);
#else
freopen("home.in","r",stdin);
freopen("home.out","w",stdout);
#endif
int T=read();
while(T--){
int n = read(), m = read();
tot = n;
dfs_clock = top = root = 0;
cle(dfn) cle(low) cle(cut) cle(sta) cle(fa) cle(depth)
cle(e) cle(g) ans.clear();
for (int i = 1; i <= m; i++) {
int u = read(), v = read();
g[u].push_back(v);
g[v].push_back(u);
}
for (int i = 1; i <= n; i++)
if (!dfn[i]) root = i, Tarjan(i), top--;
dfs(1);
for (int i = fa[n]; i != 1; i = fa[i])
if (cut[i]) ans.push_back(i);
printf("%d\n", ans.size());
sort(ans.begin(), ans.end());
int siz = ans.size();
for(int i = 0; i < siz; i++) printf("%d ", ans[i]);
puts("");
}
return 0;
}
visit


题解
- 枚举向左走了多少步,那么向右走,向上走,向下走的步数都是可以计算出来的。
- 设分别为 \(l,r,u,d\) 步,那么贡献的答案就是 \(\frac{T!}{l!r!u!d!}=\binom{T}{l}\binom{T-l}{r}\binom{T-l-r}{u}\)。
- 注意到保证 \(mod\) 的每个质因子次幂数都为 \(1\),所以 \(\text{lucas}\) 定理求出模每个质因子意义下的答案,然后 \(\text{CRT}\) 合并到一起就好了。
- 这个玩意有一个简单的式子,答案为 \(\binom{T}{\frac{T-n-m}{2}} \times \binom{T}{\frac{T-|n-m|}{2}}\)。
- 主要就是CRT的部分
code
#include <bits/stdc++.h>
using namespace std;
#define print(_) cerr << #_ << " : " << _ << endl;
const int maxn = 1e5 + 100;
#define int long long
int mod, fac[maxn], p[maxn], res[maxn];
int qpow(int x, int y, int curmod) {
int ans = 1;
for (; y; y >>= 1, (x *= x) %= curmod) if (y & 1) ans = ans * x % curmod;
return ans;
}
int C(int a, int b, int curmod) {
if (a < b) return 0;
if (b == 0 || a == b) return 1;
return fac[a] * qpow(fac[b], curmod - 2, curmod) % curmod * qpow(fac[a - b], curmod - 2, curmod) % curmod;
}
int lucas(int a, int b, int curmod) {
if (a < b) return 0;
if (b == 0) return 1;
return C(a % curmod, b % curmod, curmod) * lucas(a / curmod, b / curmod, curmod) % curmod;
}
int exgcd(int a, int b, int &x, int &y) {
if (b == 0) { x = 1, y = 0; return a; }
int d = exgcd(b, a % b, x, y);
int z = x; x = y; y = z - y * (a / b);
return d;
}
int divide(int n) {
int m = 0;
for (int i = 2; i * i <= n; i++) {
if (n % i == 0) {
p[++m] = i;
while (n % i == 0) n /= i;
}
}
if (n > 1) p[++m] = n;
return m;
}
int CRT(int num) {
int tot = 1, x = 0, y = 0;
for (int i = 1; i <= num; i++) tot *= p[i];
for (int i = 1; i <= num; i++) {
int w = tot / p[i];
int tmpx = 0;
int ny = exgcd(w, p[i], tmpx, y);
x = (x + w * res[i] * tmpx) % tot;
}
return (x + tot) % tot;
}
signed main() {
#ifdef local
freopen("in", "r", stdin);
#else
freopen("visit.in", "r", stdin);
freopen("visit.out", "w", stdout);
#endif
int T; scanf("%lld", &T);
scanf("%lld", &mod);
int n, m; scanf("%lld%lld", &n, &m);
int num = divide(mod);
for (int i = 1; i <= num; i++) {
int curmod = p[i];
fac[0] = 1;
for (int j = 1; j <= T; j++) fac[j] = fac[j - 1] * j % curmod;
res[i] = lucas(T, (T - n - m) / 2, curmod) * lucas(T, (T - abs(n - m)) / 2, curmod) % curmod;
}
cout << CRT(num) << endl;
return 0;
}
光

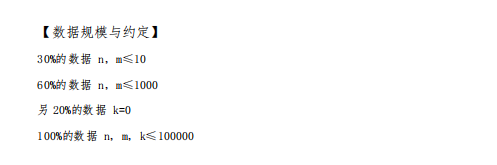
题解
- 学长题解
- 实际上对于每一个格子,光线只可能从两个方向射过来,并且这两个方向一定是对称的。
- 证明这个性质存在,可以分析光线经过的格点横纵坐标加和的奇偶性。
- 对于单步操作,会导致 \(x \pm 1,y \pm 1\),故 \(x+y\) 的奇偶性一定不变。
- 所以,光从一个点射出到同向的回到这个点,要么经过了路径上每个点两次(一去一回,即路程上遇到了反弹),要么经过了路径上每个点一次(形成一个环)。
- 只需要讨论路程上是否遇到了反弹操作,如果遇到,那么给总路程除一个 \(2\)。
- 问题就是怎么计算总路程。
- 可以发现障碍的总数是不大的,对于每个障碍至多反弹 \(4\) 次,所以反弹的总次数也是不大的。
- 所以只要能够 \(O(\log n)\) 找到下一次反弹的位置即可。
- 只要开很多个 \(\text{set}\)(对于每一条对角线开一个),就可以直接在 \(\text{set}\) 上二分找到下一个反弹的位置了,然而代码很毒瘤。
- ** 代码没写出来,,,**


 浙公网安备 33010602011771号
浙公网安备 33010602011771号