atcode abc318,codeforce 1861
题解
- AtCoder abc318_a Full Moon
- AtCoder abc318_b Overlapping sheets
- AtCoder abc318_c Blue Spring
- AtCoder abc318_d General Weighted Max Matching
- AtCoder abc318_e Sandwiches
- AtCoder abc318_f Octopus
- AtCoder abc318_g Typical Path Problem
- CodeForces 1861A Prime Deletion
- CodeForces 1861B Two Binary Strings
- CodeForces 1861C Queries for the Array
- CodeForces 1861D Sorting By Multiplication
AtCoder abc318_a Full Moon
高桥喜欢满月。
让今天成为第一天。今天或之后第一个能看到满月的日子是M天。之后,他每P天就能看到一次满月,即在M+P天、M+2P天,以此类推。
求出他能看到在第1天到第N天之间(包括第1天和第N天)的满月天数。
分析
要求 M+kP≤N 的情况下K的最大值
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10, INF = 0x3f3f3f3f;
int main() {
int n, m, p;
while (cin >> n >> m >> p) {
cout << (n - m) / p + (n >= m);
}
return 0;
}
AtCoder abc318_b Overlapping sheets
在一个坐标平面上有N个矩形薄板。
每个薄片覆盖的矩形区域的每一侧都平行于x轴或y轴。
具体地说,第i张恰好覆盖了满足Ai≤x≤Bi和Ci≤y≤Di的区域。
设S是由一个或多个片材覆盖的区域的面积。可以证明,在约束条件下,S是一个整数。
打印一个整数S。
分析
标记思想,st[i][j]=1表示点(i,j) 被覆盖。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 110, INF = 0x3f3f3f3f;
int main() {
int n, a, b, c, d;
while (cin >> n) {
vector<vector<bool>> s(100, vector<bool>(100, 0));
for (int i = 1; i <= n; i++) {
cin >> a >> b >> c >> d;
for (int x = a; x < b; x++)
for (int y = c; y < d; y++) s[x][y] = 1;
}
int res = 0;
n = 100;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++) res += s[i][j];
cout << res << endl;
}
return 0;
}
AtCoder abc318_c Blue Spring
Takahashi 正在计划一次为期N天的火车旅行。
对于每一天,他可以支付常规票价或使用一天通行证。
这里,对于1≤i≤N,行程第i天的常规票价为Fi日元。
另一方面,一批每份D张的一天通行证的售价为P日元。您可以购买任意数量的通行证,但只能以D为单位。
购买的每张通行证可以在任何一天使用,旅行结束时吃一些剩菜也没关系。
找到N日游的最低可能总成本,即购买一天通行证的成本加上一天通行证未涵盖天数的常规总票价。
分析
如果购买通行证的费用比常规票价便宜,那就购买通行证,所以可以先排序。
需要注意通行证是每d天作为一个单位购买。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 110, INF = 0x3f3f3f3f;
int main() {
int n, d, p;
while (cin >> n >> d >> p) {
vector<int> f(n);
for (int i = 0; i < n; i++) cin >> f[i];
sort(f.begin(), f.end(), greater<int>());
LL s = 0, res = 0;
for (int i = 0; i < n; i++) {
s += f[i];
if ((i + 1) % d == 0 || i == n - 1)
res += min(1ll * p, s), s = 0;
}
cout << res << endl;
}
return 0;
}
AtCoder abc318_d General Weighted Max Matching
给出了一个加权无向完全图,其中N个顶点编号从1到N。连接顶点 i 和 j (i<j) 的边的权重为\(D_{i,j}\)。
当在以下条件下选择一定数量的边时,找到所选边的最大可能总权重。
- 所选边的端点是两两不同。
分析
对于数据量20左右题目,可以考虑复杂度 \(2^n, n!\)的算法,如搜索剪枝,状压dp(二进制枚举)的算法,
-
搜索边:很直观的想法就是对于每条边,可以选也可以不选,共有 \(m=\sum_{i=1}^{n-1} i=120\),如果单纯枚举,有 \(2^{120}\) 种方案,会超时;考虑剪枝,但是无法证明剪枝后的效率可靠。
-
搜索点:因为点的数量较小,那么考虑搜索每个点选或不选,同时每个点连接 \(n-1\) 条边,复杂度 \(O(2^{n}✖n^2)\)
-
状态压缩dp:所谓状压dp就是用二进制来表示当前状态/或者说当前方案.
1) 状态定义:\(dp_[i]\) 表示当前方案为 i 时的最优解。
如:i=15(10)=1111(2) 表示已选择编号为 1,2,3,4的点。
2)状态转移:\(dp_{[k|s]} =max(dp_{[k|s]}, dp_{[k]}+w)\)
其中 s=(1<<i)|(1<<j) 表示选择的两个点,w 为连接这两个点的边的权值。
如果可以由状态s转移过来,那么之前一定没有选择这两个点,也就是 k&s=0。
比如:s=0000 1100(2),意味着当前选择的是编号为 3,4 的点;那么 k 一定不包含这两个点,也就是 k=xxxx 00xx,此时 k&s=0,证明可以从 s 转移到 k|s。
3)最终目标:每次选择两个点,那么最后目标就是所有选两个点(二进制有偶数个1)的状态的最大值,也可以在每次转移时维护答案。
4)复杂度分析: 任意两个点的组合情况为 \(C_n^2\) 种,所有的状态情况有 \(2^{n}-1\) 种,所以整体复杂度为 \(O(2^n✖n^2)\).
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 20;
int n, m, d[N][N];
struct T {
int u, v, w;
bool operator<(const T& t) const { return w > t.w; }
};
vector<T> g;
vector<bool> st(N);
vector<LL> sum(N);
LL res;
// ------------------------------------------------
void dfs(int x, LL s) {
res = max(res, s);
if (x >= g.size())
return;
// if (s + sum[g.size() - 1] - sum[x - 1] <= res)
// return; // 企图搞一个剪枝,最后剪废了
int u = g[x].u, v = g[x].v, w = g[x].w;
if (st[u] + st[v] == 0) {
st[u] = st[v] = 1, dfs(x + 1, s + w);
st[u] = st[v] = 0;
}
dfs(x + 1, s);
}
int solve1() {
while (cin >> n) {
g.clear(), st.clear(), sum.clear(), res = 0;
// g.push_back({0, 0, 0});
for (int i = 1, x; i <= n - 1; i++)
for (int j = i + 1; j <= n; j++) {
cin >> x;
g.push_back({i, j, x});
}
sort(g.begin(), g.end());
// for (int i = 1; i <= n; i++)
// sum[i] = sum[i - 1] + g[i].w;
dfs(0, 0);
cout << res << endl;
}
return 0;
}
// ------------------------------------------------
void dfs2(int x, LL s) {
res = max(res, s);
if (x > n)
return;
if (st[x]) {
dfs2(x + 1, s);
return;
}
for (int i = x + 1; i <= n; i++) {
if (!st[i]) {
st[x] = st[i] = 1, dfs2(x + 1, s + d[x][i]);
st[x] = st[i] = 0;
}
}
dfs2(x + 1, s);
}
int solve2() {
while (cin >> n) {
g.clear(), st.clear(), res = 0;
for (int i = 1, x; i <= n - 1; i++)
for (int j = i + 1; j <= n; j++) {
cin >> x;
d[i][j] = x;
}
dfs2(1, 0);
cout << res << endl;
}
return 0;
}
// ------------------------------------------------
int solve3() {
while (cin >> n) {
vector<LL> dp(1 << n);
res = 0;
for (int i = 0, x; i < n; i++)
for (int j = i + 1; j < n; j++) {
cin >> x;
int s = (1 << i) | (1 << j);
for (int k = 0; k < (1 << n); k++)
if (!(k & s)) {
dp[k | s] = max(dp[k | s], dp[k] + x);
res = max(res, dp[k | s]);
}
}
cout << res << endl;
}
return 0;
}
int main() {
// solve1();
// solve2();
solve3();
return 0;
}
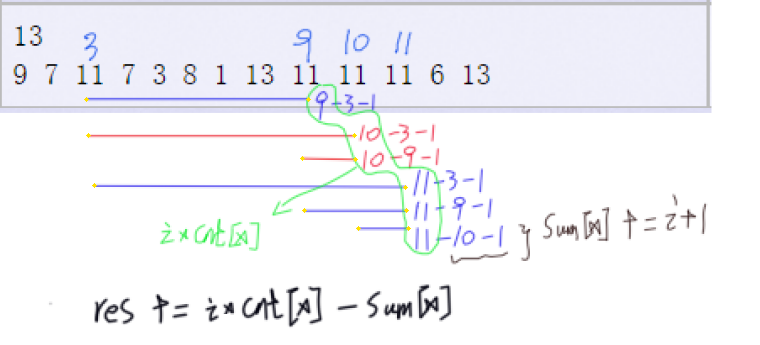
AtCoder abc318_e Sandwiches
给出了一个长度为N: A=(A1,A2,...,AN)的正整数序列。
求满足以下条件的正整数 (i,j,k) 三元组数:
- 1≤i<j<k≤ N,Ai=Ak, Ai≠Aj.
分析
直接枚举i,j,k会TLE,当我们看数据的时候其实会发现,出现一个数据就可以确定该数据对答案的贡献,那么也就是说存在 \(O(n)\) 的解法--- 当然,这是一种感性的直觉。
- 如果 找到 Ai=Ak 的数量,以及 Ai=Aj=Ak 的数量,那么两者的差值就是答案。
1)Ai=Ak的数量可以通过模拟样例找到如下图的规律求得。
通过模拟样例,可以发现,每个元素的贡献.
![image]()
2)Ai=Aj=Ak 的数量可以通过组合数求的,即在 cnt[x] 个数中任选3个数进行组合 \(C_n^3\).
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 3e5 + 10, INF = 0x3f3f3f3f;
int T = 1, n;
int main() {
while (cin >> n) {
LL res = 0;
vector<LL> cnt(n + 1, 0), sum(n + 1, 0);
for (int i = 1, x; i <= n; i++) {
cin >> x;
res += i * cnt[x] - sum[x];
++cnt[x], sum[x] += i + 1;
}
for (int i = 1; i <= n; i++) {
LL m = cnt[i];
res -= m * (m - 1) * (m - 2) / 6;
}
cout << res << endl;
}
return 0;
}
AtCoder abc318_f Octopus
数轴线上有一个章鱼形状的机器人和N个宝藏。第 i 个宝藏(1≤i≤N)位于坐标 Xi。
机器人有一个头和 N 条腿,第 i 条腿(1≤i≤N)的长度为 Li。
找到多少个整数k,使得机器人在满足如下要求时可以抓取N个宝藏。
- 将头部放置在坐标 k 处。
- 对于 i=1,2,…,N,按顺序重复以下步骤:如果在距离头部 Li 的距离内,即在满足 k−Li≤x≤k+Li 的坐标x处,有一个宝藏尚未被抓住,则选择一个这样的宝藏并抓住它。
分析
点击查看代码
AtCoder abc318_g Typical Path Problem
给出了一个具有N顶点和M边的简单连通无向图G。G的顶点和边分别编号为顶点1、顶点2、…、顶点N和边1、边2、…、边M,并且边 i(1≤i≤M)连接顶点 $U_i$ 和 $V_i$。
G上还有不同的顶点 A、B、C。
确定是否有一条简单的路径通过顶点 B 连接顶点 A 和 C。
什么是简单连通无向图?
当G是简单且连通的无向图时,图G被称为简单连通无向图。 当图G的边没有方向时,称其为无向图。 当图G不包含自循环或多边时,图G是简单的。 当一个人可以经由边在G的所有顶点之间行进时,图G是连接的。通过顶点Z的简单路径是什么?
对于图G上的顶点X和Y,连接X和Y的简单路径是不同顶点(v1,v2,…,vk)的序列,使得$v_1=X,v_k=Y$,并且对于满足 1≤i≤k−1 的每个整数 i,G上存在连接顶点 $v_i$ 和 $v_{i+1}$ 的边。当存在满足 $v_i=Z$ 的 i(2≤i≤k−1)时,称简单路径($v_1,v_2,...,v_k$)通过顶点Z。分析
点击查看代码
CodeForces 1861A Prime Deletion
素数是一个正整数,它正好有两个不同的正因子:1和整数本身。例如,2,3,13和101是素数;1,4,6和42不是。
你会得到一个从1到9的数字序列,其中从1到9的每个数字都只出现一次。
您可以多次(可能为零)执行以下操作:从序列中选择任意一位数字并将其删除。但是,如果序列仅由两位数字组成,则无法执行此操作。
你的目标是得到一个表示素数的序列。请注意,不能对序列中的数字进行重新排序。
打印结果序列,或者报告无法执行操作,从而使结果序列为素数。
分析
首先,这是个直觉题,其次也可以正常暴力。
-
直觉,有很强烈的感觉,这个可以通过两个数的先后确定是否构成素数,那么就需要找到这样的数,发现 31,13都是素数,那么也就是说只要含1,3无论先后都能构成素数,输出结果为1,3构成的子序列,复杂度 \(O(9T)\)。
-
暴力,暴力枚举选或不选,在这里就是删或不删,共有\(2^9\)种方案,复杂都为 :\(O(2^9*T)\)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10, INF = 0x3f3f3f3f;
int main() {
int T;
string s;
cin >> T;
while (T--) {
cin >> s;
int res = (s.find('1') < s.find('3')) ? 13 : 31;
cout << res << endl;
}
return 0;
}
CodeForces 1861B Two Binary Strings
您得到两个长度相等的字符串a和b,仅由字符0和/或1组成;两个字符串都以字符0开头,以字符1结束。
您可以执行以下操作任意次数(可能为零):
- 选择其中一个字符串和该字符串中两个相等的字符;然后将它们之间的所有字符转换为这些字符。
形式上,您从这两个字符串中选择一个(设所选字符串为s),然后选择两个整数 l 和 r,使1≤l<r≤|s|和 sl=sr,然后用 sl 替换 满足 l<i<r 的每个字符 si。
例如,如果选择的字符串是 010101,则可以通过应用一个操作将其转换为以下字符串之一:
- $000101$ if you choose $l = 1$ and $r = 3$;
- $000001$ if you choose $l = 1$ and $r = 5$;
- $010001$ if you choose $l = 3$ and $r = 5$;
- $010111$ if you choose $l = 4$ and $r = 6$;
- $011111$ if you choose $l = 2$ and $r = 6$;
- $011101$ if you choose $l = 2$ and $r = 4$.
您必须确定是否可以通过多次应用此操作来使给定的字符串相等。
分析
开头必为0,结尾必为1。
那么分析发现,如果两个字符串存在相同位置为"01",则必然构成相同串。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10, INF = 0x3f3f3f3f;
int main() {
int T;
string a, b;
cin >> T;
while (T--) {
cin >> a >> b;
bool ok = 0;
for (int i = 0; i < a.size(); i++) {
if (a[i] == b[i] && a[i] == '0'
&& a[i + 1] == b[i + 1] && a[i + 1] == '1') {
ok = 1;
break;
}
}
cout << (ok ? "YES" : "NO") << endl;
}
return 0;
}
CodeForces 1861C Queries for the Array
分析
点击查看代码
CodeForces 1861D Sorting By Multiplication
分析
点击查看代码



 浙公网安备 33010602011771号
浙公网安备 33010602011771号