P1498 南蛮图腾-递归，递推

P1498 南蛮图腾

题目描述

给定一个正整数 \(n\)，参考输出样例，输出图形。

输入格式

每个数据输入一个正整数 \(n\)，表示图腾的大小（此大小非彼大小）

输出格式

这个大小的图腾

样例 #1

样例输入 #1

2

样例输出 #1

   /\
  /__\
 /\  /\
/__\/__\

样例 #2

样例输入 #2

3

样例输出 #2

       /\
      /__\
     /\  /\
    /__\/__\
   /\      /\
  /__\    /__\
 /\  /\  /\  /\
/__\/__\/__\/__\

提示

数据保证，\(1 \leq n \leq 10\)。

分析

个人觉得这是一道经典的题目，可以使用递归或是递推解决，但是都需要找到规律，此题与 P5461 赦免战俘 具有很大的相似性，建议可以同时完成。

递归

根据题目描述，将图形分为三个部分上左右，如下图，对于每一个部分发现其实还是相同的问题，但是问题的规模减小。

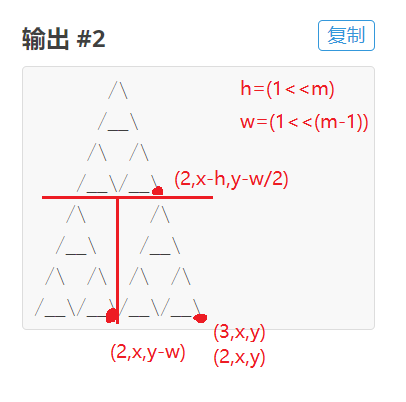
定义状态：slove(m,x,y)
以 (x,y) 作为终点的规模为 m 的问题，可以分解为三个子问题。
即如下递归关系式：
    slove(m - 1, x, y);
    slove(m - 1, x, y - w);
    slove(m - 1, x - h, y - w / 2);
其中：h,w 分别为当规模为 (m-1)时，图形的高，宽

递归出口：当 m=1时，结束。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 4400, INF = 0x3f3f3f3f;
char s[N][N];  // 1<<n   1024*4

void slove(int m, int x, int y) {
    int h = (1 << (m - 1)), w = 4 * (1 << (m - 2));
    // printf("slove(%d,%d,%d)\nh=%d, w=%d\n", m, x, y, h, w);
    if (m == 1) {
        s[x - 1][y - 3] = ' ', s[x - 1][y - 2] = '/', s[x - 1][y - 1] = '\\', s[x - 1][y] = ' ';
        s[x][y - 3] = '/', s[x][y - 2] = '_', s[x][y - 1] = '_', s[x][y] = '\\';
        return;
    }
    slove(m - 1, x, y);
    slove(m - 1, x, y - w);
    slove(m - 1, x - h, y - w / 2);
}
int main() {
    // freopen("data.in", "r", stdin);
    int n;
    while (~scanf("%d", &n)) {
        int x = (1 << n), y = 4 * (1 << (n - 1));
        for (int i = 1; i <= x; i++)
            for (int j = 1; j <= y; j++) s[i][j] = ' ';
        slove(n, x, y);
        for (int i = 1; i <= x; i++) {
            for (int j = 1; j <= y; j++) putchar(s[i][j]);
            puts("");
        }
    }
    return 0;
}

递推

#include <bits/stdc++.h>
using namespace std;
const int N = 4400;
int n;
char mp[N][N], a[N][N];

void init() {
    for (int i = 0; i < N; i++)
        for (int j = 0; j < N; j++) a[i][j] = ' ', mp[i][j] = ' ';
    int x = 1, y = 3;
    a[x - 1][y - 3] = ' ', a[x - 1][y - 2] = '/', a[x - 1][y - 1] = '\\', a[x - 1][y] = ' ';
    a[x][y - 3] = '/', a[x][y - 2] = '_', a[x][y - 1] = '_', a[x][y] = '\\';
}

void slove() {
    int l = 4, h = 2;
    for (int t = 2; t <= n; t++) {
        for (int i = 0; i < N; i++)
            for (int j = 0; j < N; j++) mp[i][j] = ' ';
        int x = 0, y = l / 2;
        for (int i = 0; i < h; i++)
            for (int j = 0; j < l; j++) mp[x + i][y + j] = a[i][j];
        x = h, y = 0;
        for (int i = 0; i < h; i++)
            for (int j = 0; j < l; j++) mp[x + i][y + j] = a[i][j];
        x = h, y = l;
        for (int i = 0; i < h; i++)
            for (int j = 0; j < l; j++) mp[x + i][y + j] = a[i][j];
        h *= 2, l *= 2;
        for (int i = 0; i < h; i++)
            for (int j = 0; j < l; j++) a[i][j] = mp[i][j];
    }
    for (int i = 0; i < h; i++) {
        for (int j = 0; j < l; j++) cout << a[i][j];
        cout << endl;
    }
}
int main() {
    while (cin >> n) {
        init();
        slove();
    }
    return 0;
}