第1部分 基础算法(提高篇)-->第1章 贪心算法
贪心算法
1422:【例题1】活动安排
【题目描述】
设有 n 个活动的集合 E={1,2,…,n},其中每个活动都要求使用同一资源,
如演讲会场等,而在同一时间内只有一个活动能使用这一资源。
每个活动 i 都有一个要求使用该资源的起始时间 si 和一个结束时间 fi,且 si<fi。
如果选择了活动 i,则它在半开时间区间 [si,fi) 内占用资源。
若区间 [si,fi) 与区间 [sj,fj) 不相交, 则称活动 i 与活动 j 是相容的。
也就是说,当 si ≥fj 或 sj ≥fi 时,活动 i 与活动 j 相容。
选择出由相互兼容的活动组成的最大集合。
【输入】
第 1 行一个整数 n(n≤1000),接下来 n 行,每行两个整数 si 和 fi。
【输出】
输出尽可能多的互相兼容的活动个数。
【输入样例】
4
1 3
4 6
2 5
1 7
【输出样例】
2
【题解】
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
struct T{
int s,f;
}t[N];
bool cmp(T a, T b){
return a.f<b.f;
}
int main(){
int n, cnt=1; scanf("%d", &n);
for(int i=0; i<n; i++){
scanf("%d%d", &t[i].s, &t[i].f);
}
sort(t, t+n, cmp);
int end=t[0].f;
for(int i=1; i<n; i++){
if(t[i].s>=end){
cnt++;
end = t[i].f;
}
}
printf("%d", cnt);
return 0;
}
1423:【例题2】种树
【题目描述】
现在我们国家开展新农村建设,农村的住房建设纳入了统一规划,统一建设,政府要求每一住户门口种些树。
门口路边的地区被分割成块,并被编号成 1..N。
每个部分为一个单位尺寸大小并最多可种一棵树。
每个居民房子门前被指定了三个号码B,E,T。
这三个数表示该居民想在 B 和 E 之间最少种 T 棵树。
当然,B≤E,居民必须记住在指定区不能种多于区域地块数的树,所以 T ≤E-B+l。
居民们想种树的各自区域可以交叉。
你的任务是求出能满足所有要求的最少的树的数量,尽量较少政府的支出。
【输入】
第一行包含数据N,M,区域的个数 (0<N≤30000),房子的数目 (0<m≤5000);
下面的m行描述居民们的需要:B E T,0<B≤E≤30000,T≤E-B+1。
【输出】
输出一个数,为满足所有居民的要求,所需要种树的最少数量。
【输入样例】
9 4
3 5 2
1 4 2
4 6 2
8 9 2
【输出样例】
5
【题解】
#include<bits/stdc++.h>
using namespace std;
const int N=3e4+10;
bool used[N];
struct T{
int s,f,v;
}t[N];
bool cmp(T a, T b){
return a.f<b.f;
}
int main(){
int n,m,ans=0; scanf("%d%d", &n, &m);
for(int i=0; i<m; i++){
scanf("%d%d%d", &t[i].s, &t[i].f, &t[i].v);
}
sort(t, t+m, cmp);
for(int i=0; i<m; i++){
int cnt=0;
for(int j=t[i].s; j<=t[i].f; j++){
if(used[j]) cnt++;
}
if(cnt>=t[i].v) continue;
for(int j=t[i].f; j>=t[i].s; j--){
if(!used[j]){
used[j]=1; cnt++; ans++;
}
if(cnt==t[i].v) break;
}
}
printf("%d\n", ans);
return 0;
}
1424:【例题3】喷水装置
【题目描述】
长 L 米,宽 W 米的草坪里装有 n 个浇灌喷头。每个喷头都装在草坪中心线上(离两边各 W2 米)。我们知道每个喷头的位置(离草坪中心线左端的距离),以及它能覆盖到的浇灌范围。
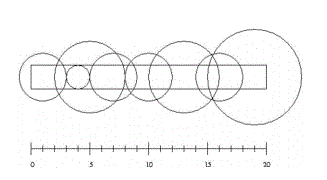
请问:如果要同时浇灌整块草坪,最少需要打开多少个喷头?
【输入】
输入包含若干组测试数据。
第一行一个整数 T 表示数据组数;
每组数据的第一行是整数 n、L 和 W;
接下来的 n 行,每行包含两个整数,给出一个喷头的位置和浇灌半径(上面的示意图是样例输入第一组数据所描述的情况)。
【输出】
对每组测试数据输出一个数字,表示要浇灌整块草坪所需喷头数目的最小值。如果所有喷头都打开也不能浇灌整块草坪,则输出 −1 。
【输入样例】
3
8 20 2
5 3
4 1
1 2
7 2
10 2
13 3
16 2
19 4
3 10 1
3 5
9 3
6 1
3 10 1
5 3
1 1
9 1
【输出样例】
6
2
-1
数据范围:对于 100% 的数据,n≤15000。
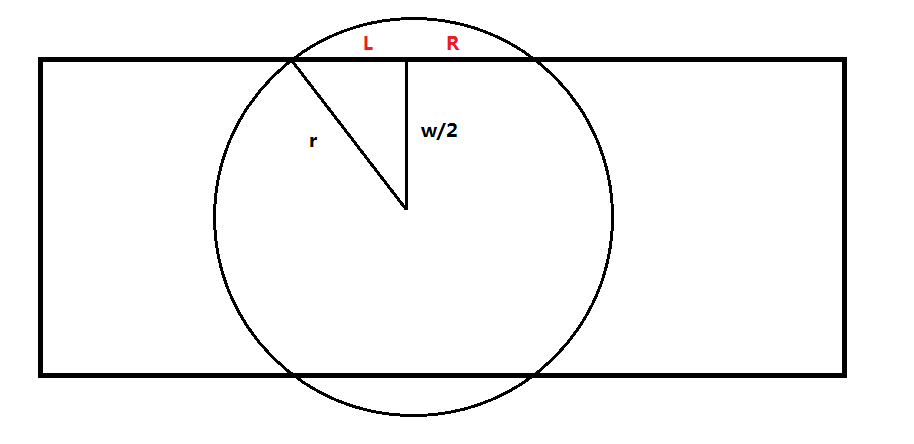
- 分析:先画个图,求出每个喷头左右能到的最远距离,\(L=\sqrt{r^2-{(\frac{w}{2})}^2}\)
![image]()
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e6+10, INF=0x3f3f3f3f;
struct T {
double l,r;
bool operator< (const T& rhs) const {
return l < rhs.l;
}
} a[N];
int main() {
// freopen("data.in", "r", stdin);
int t; cin>>t;
while(t--) {
int n,l,w,d,r,cnt=0,ans=0;
cin>>n>>l>>w;
for(int i=1; i<=n; i++) {
cin>>d>>r;
if(1.0*r < w/2.0) continue;
a[++cnt].l = d-sqrt(r*r-w*w/4.0);
a[cnt].r = d+sqrt(r*r-w*w/4.0);
}
sort(a+1, a+1+cnt);
double st=0, end=0; int p=1;
while(st < l) {
end=st;
while(a[p].l<end && p<=cnt) {
if(a[p].r>st) st=a[p].r;
p++;
}
if(st==end&&st<l) { ans=-1; break; }
ans++;
}
cout<<ans<<endl;
}
return 0;
}
1425:【例题4】加工生产调度
【题目描述】
某工厂收到了 n 个产品的订单,这 n 个产品分别在 A、B 两个车间加工,并且必须先在 A 车间加工后才可以到 B 车间加工。
某个产品 i 在 A,B 两车间加工的时间分别为Ai,Bi。怎样安排这 n 个产品的加工顺序,才能使总的加工时间最短。
这里所说的加工时间是指:从开始加工第一个产品到最后所有的产品都已在 A,B 两车间加工完毕的时间。
【输入】
第一行仅—个数据 n ,表示产品的数量;
接下来 n 个数据是表示这 n 个产品在 A 车间加工各自所要的时间;
最后的 n 个数据是表示这 n 个产品在 B 车间加工各自所要的时间。
【输出】
第一行一个数据,表示最少的加工时间;
第二行是一种最小加工时间的加工顺序。
【输入样例】
5
3 5 8 7 10
6 2 1 4 9
【输出样例】
34
1 5 4 2 3
【提示】对于100%的数据, 0 < n < 10000,所有数值皆为整数。
1426:【例题5】智力大冲浪
【题目描述】
小伟报名参加中央电视台的智力大冲浪节目。
本次挑战赛吸引了众多参赛者,主持人为了表彰大家的勇气,先奖励每个参赛者 m 元。
先不要太高兴!因为这些钱还不一定都是你的。
接下来主持人宣布了比赛规则:
首先,比赛时间分为 n 个时段 (n≤500),它又给出了很多小游戏,
每个小游戏都必须在规定期限 ti 前完成 (1≤ti≤n)。
如果一个游戏没能在规定期限前完成,则要从奖励费m元中扣去一部分钱 wi,wi 为自然数,
不同的游戏扣去的钱是不一样的。
当然,每个游戏本身都很简单,保证每个参赛者都能在一个时段内完成,而且都必须从整时段开始。
主持人只是想考考每个参赛者如何安排组织自己做游戏的顺序。
作为参赛者,小伟很想赢得冠军,当然更想赢取最多的钱!
注意:比赛绝对不会让参赛者赔钱!
【输入】
输入共 4 行。
第一行为 m,表示一开始奖励给每位参赛者的钱;
第二行为 n,表示有 n个小游戏; 第三行有 n 个数,分别表示游戏 1~n 的规定完成期限;
第四行有 n 个数,分别表示游戏 1~n 不能在规定期限前完成的扣款数。
【输出】
仅 1 行。表示小伟能赢取最多的钱。
【输入样例】
10000
7
4 2 4 3 1 4 6
70 60 50 40 30 20 10
【输出样例】
9950
【数据范围】n≤500,1≤ti≤n
【题解】
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
bool vis[N];
struct T{
int t,w;
}t[N];
bool cmp(T a, T b){
if(a.w!=b.w) return a.w>b.w;
return a.t<b.t;
}
int main(){
// freopen("data.in", "r", stdin);
int m,n; scanf("%d%d", &m, &n);
for(int i=0; i<n; i++) scanf("%d", &t[i].t);
for(int i=0; i<n; i++) scanf("%d", &t[i].w);
sort(t, t+n, cmp);
int ans=0;
for(int i=0; i<n; i++){
bool flag=0;
for(int j=t[i].t; j>=1; j--){
if(!vis[j]){
vis[j]=1; flag=1; break;
}
}
if(!flag){
ans+=t[i].w;
}
}
printf("%d\n", m-ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号