chapter_3 栈和队列
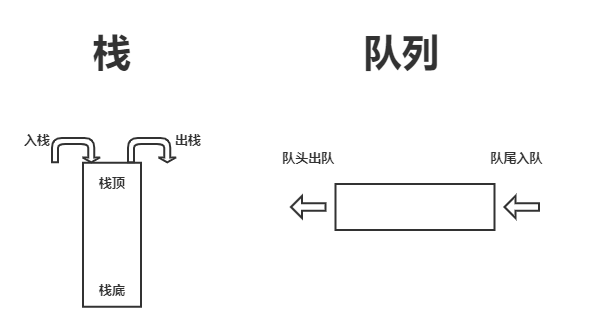
栈
栈是一种只能在一端进行插入或删除操作的线性表。
允许进行插入、删除操作的一端称为栈顶。
表的另一端称为栈底。
当栈中没有数据元素时,称为空栈。
栈的插入操作通常称为进栈或入栈。
栈的删除操作通常称为退栈或出栈。
栈的主要特点是“后进先出”,即后进栈的元素先出栈。栈也称为后进先出表。
【例】设一个栈的输入序列为 a,b,c,d,则借助一个栈所得到的输出序列不可能是( )。
A. c,d,b,a
B. d,c,b,a
C. a,c,d,b
D. d,a,b,c
答案:D
【例】一个栈的入栈序列为 1,2,3,…,n,其出栈序列是 p1, p2,p3, …, pn。
若 p2=3,则 p3 可能取值的个数是( )多少?
A.n-3
B.n-2
C.n-1
D. 无法确定
答案:C
p3可以取1:1进,2进,2出,3进,3出,1出,…。
p3可以取2:1进,1出,2进,3进,3出,2出,… 。
p3可以取4:1进,1出,2进,3进,3出,4进,4出, … 。
p3可以取5:1进,1出,2进,3进,3出,4进,5进,5出, … 。
...
p3可以取除了3外的任何值。
ADT Stack{
数据对象:D={ di | 0≤i≤n,n为一个正整数}
数据关系:无
基本运算:
InitStack(s) :初始化栈。构造一个空栈s。
DestroyStack(s) :销毁栈。释放栈s占用的存储空间。
StackEmpty(s) :判断栈是否为空:若栈s为空,则返回真;否则返回假。
Push(S,e) :进栈。将元素e插入到栈s中作为栈顶元素。
Pop(s,e) :出栈。从栈s中退出栈顶元素,并将其值赋给e。
GetTop(s,e) :取栈顶元素。返回当前的栈顶元素,并将其值赋给e。
}
顺序栈
#include <stdio.h>
#include <stdlib.h>
#define bool int
#define true 1
#define false 0
#define ElemType int
#define MaxSize 10001
typedef struct {
ElemType data[MaxSize];
int top; //栈顶指针
} SqStack;
//(1)初始化栈InitStack(s)
void InitStack(SqStack *s) {
s->top=-1;
}
//(2)销毁栈DestroyStack(s)
void DestroyStack(SqStack *s) {
free(s);
}
//(3)判断栈是否为空StackEmpty(s)
bool StackEmpty(SqStack *s) {
return(s->top==-1);
}
//(4)进栈Push(s,e)
bool Push(SqStack *s,ElemType e) {
if (s->top==MaxSize-1){ //栈满的情况,即栈上溢出
return false;
}
s->top++; //栈顶指针增1
s->data[s->top]=e; //元素e放在栈顶指针处
return true;
}
//(5)出栈Pop(s,e)
bool Pop(SqStack *s,ElemType *e) {
if (s->top==-1){ //栈为空的情况,即栈下溢出
return false;
}
*e=s->data[s->top]; //取栈顶指针元素的元素
s->top--; //栈顶指针减1
return true;
}
//(6)取栈顶元素GetTop(s,e)
bool GetTop(SqStack *s,ElemType *e) {
if (s->top==-1) { //栈为空的情况,即栈下溢出
return false;
}
*e=s->data[s->top]; //取栈顶指针元素的元素
return true;
}
int main() {
int a[]={1,2,3,4,5,6};
int n = sizeof(a)/sizeof(int), i, e;
printf("n = %d\n", n);
SqStack* sta=(SqStack*)malloc(sizeof(SqStack));
InitStack(sta);
for(i=0; i<n; i++){
Push(sta, a[i]);
}
while(!StackEmpty(sta)){
bool flag = Pop(sta, &e);
printf("%d ", flag ? e : -1);
}
return 0;
}
链栈
采用链表存储的栈称为链栈,这里采用带头结点的单链表实现。
【例】编写一个算法判断输入的表达式中括号是否配对(假设只含有左、右圆括号)。
#include <stdio.h>
#include <stdlib.h>
#define bool int
#define true 1
#define false 0
#define ElemType char
#define MaxSize 10001
typedef struct linknode {
ElemType data; //数据域
struct linknode *next; //指针域
} LinkStNode;
//(1)初始化栈InitStack(s)
void InitStack(LinkStNode *s) {
s->next=NULL;
}
//(2)销毁栈DestroyStack(s)
void DestroyStack(LinkStNode *s) {
LinkStNode *p=s,*q=s->next;
while (q!=NULL) {
free(p);
p=q;
q=p->next;
}
free(p); //此时p指向尾结点,释放其空间
}
//(3)判断栈是否为空StackEmpty(s)
bool StackEmpty(LinkStNode *s) {
return(s->next==NULL);
}
//(4)进栈Push(s,e)
void Push(LinkStNode *s,ElemType e) {
LinkStNode *p;
p=(LinkStNode *)malloc(sizeof(LinkStNode));
p->data=e; //新建元素e对应的结点p
p->next=s->next; //插入p结点作为开始结点
s->next=p;
}
//(5)出栈Pop(s,e)
bool Pop(LinkStNode *s,ElemType *e) {
LinkStNode *p;
if (s->next==NULL) { //栈空的情况
return false;
}
p=s->next; //p指向开始结点
*e=p->data;
s->next=p->next; //删除p结点
free(p); //释放p结点
return true;
}
//(6)取栈顶元素GetTop(s,e)
bool GetTop(LinkStNode *s,ElemType *e) {
if (s->next==NULL) { //栈空的情况
return false;
}
*e=s->next->data;
return true;
}
bool Match(char exp[],int n) {
int i=0;
char e;
bool match=true;
LinkStNode *st;
InitStack(st); //初始化栈
while (i<n && match) { //扫描exp中所有字符
if (exp[i]=='(' ) Push(st,exp[i]);
else if (exp[i]==')') { //当前字符为右括号
if (GetTop(st,&e)==true) {
if (e!='(') match=false; //栈顶元素不为'('时不匹配
else Pop(st,&e); //将栈顶元素出栈
} else match=false; //无法取栈顶元素时不匹配
}
i++; //继续处理其他字符
}
if (!StackEmpty(st)) match=false;
DestroyStack(st); //销毁栈
return match;
}
int main() {
char a[]="(()))", e;
int n = sizeof(a)/sizeof(char)-1, i;
printf("n = %d\n", n);
LinkStNode* sta=(LinkStNode *)malloc(sizeof(LinkStNode));
InitStack(sta);
for(i=0; i<n; i++) {
Push(sta, a[i]);
}
while(!StackEmpty(sta)) {
bool flag = Pop(sta, &e);
printf("%c ", flag ? e : '0');
}
bool flag = Match(a, n);
printf("\nflag = %d\n", flag);
return 0;
}
表达式求值问题
【例】用户输入一个包含 "+-*/"、正整数和圆括号的合法算术表达式,计算该表达式的运算结果。
前缀表达式:+ 1 * 2 3
中缀表达式:1 + 2 * 3
后缀表达式:1 2 3 * +
后缀表达式又称逆波兰表达式
#include <stdio.h>
#include <stdlib.h>
#define bool int
#define true 1
#define false 0
#define ElemType char
#define MaxSize 10001
typedef struct {
ElemType data[MaxSize];
int top; //栈顶指针
} SqStack;
//(1)初始化栈InitStack(s)
void InitStack(SqStack *s) {
s->top=-1;
}
//(2)销毁栈DestroyStack(s)
void DestroyStack(SqStack *s) {
free(s);
}
//(3)判断栈是否为空StackEmpty(s)
bool StackEmpty(SqStack *s) {
return(s->top==-1);
}
//(4)进栈Push(s,e)
bool Push(SqStack *s,ElemType e) {
if (s->top==MaxSize-1) { //栈满的情况,即栈上溢出
return false;
}
s->top++; //栈顶指针增1
s->data[s->top]=e; //元素e放在栈顶指针处
return true;
}
//(5)出栈Pop(s,e)
bool Pop(SqStack *s,ElemType *e) {
if (s->top==-1) { //栈为空的情况,即栈下溢出
return false;
}
*e=s->data[s->top]; //取栈顶指针元素的元素
s->top--; //栈顶指针减1
return true;
}
//(6)取栈顶元素GetTop(s,e)
bool GetTop(SqStack *s,ElemType *e) {
if (s->top==-1) { //栈为空的情况,即栈下溢出
return false;
}
*e=s->data[s->top]; //取栈顶指针元素的元素
return true;
}
//将算术表达式exp转换成后缀表达式postexp。
void trans(char exp[],char postexp[]) {
char e;
SqStack *sta=(SqStack*)malloc(sizeof(SqStack)); //定义运算符栈指针
InitStack(sta); //初始化运算符栈
int i=0; //i作为postexp的下标
while (*exp!='\0') { //exp表达式未扫描完时循环
switch(*exp) {
case '(': { //判定为左括号
Push(sta,'('); //左括号进栈
exp++; //继续扫描其他字符
break;
}
case ')': { //判定为右括号
Pop(sta,&e); //出栈元素e
while (e!='(') { //不为'('时循环
postexp[i++]=e; //将e存放到postexp中
Pop(sta,&e); //继续出栈元素e
}
exp++; //继续扫描其他字符
break;
}
case '+': //判定为加或减号
case '-': {
while (!StackEmpty(sta)) { //栈不空循环
GetTop(sta,&e); //取栈顶元素e
if (e!='(') { //e不是'('
postexp[i++]=e; //将e存放到postexp中
Pop(sta,&e); //出栈元素e
} else //e是'(时退出循环
break;
}
Push(sta,*exp); //将'+'或'-'进栈
exp++; //继续扫描其他字符
break;
}
case '*': //判定为'*'或'/'号
case '/': {
while (!StackEmpty(sta)) { //栈不空循环
GetTop(sta,&e); //取栈顶元素e
if (e=='*' || e=='/') {
postexp[i++]=e; //将e存放到postexp中
Pop(sta,&e); //出栈元素e
} else break; //e为非'*'或'/'运算符时退出循环
}
Push(sta,*exp); //将'*'或'/'进栈
exp++; //继续扫描其他字符
break;
}
default: {//处理数字字符
while (*exp>='0' && *exp<='9') {//判定为数字字符
postexp[i++]=*exp;
exp++;
}
postexp[i++]='#';//用#标识一个数值串结束
}
}
}
while (!StackEmpty(sta)) { //此时exp扫描完毕,栈不空时循环
Pop(sta, &e); //出栈元素e
postexp[i++]=e; //将e存放到postexp中
}
postexp[i]='\0'; //给postexp表达式添加结束标识
DestroyStack(sta); //销毁栈
}
//计算后缀表达式postexp的值。
/*double compvalue(char *postexp) {
double d, a, b, c, e=0;
SqStack *sta=(SqStack*)malloc(sizeof(SqStack)); //定义操作数栈
InitStack(sta); //初始化操作数栈
while (*postexp!='\0') {//postexp字符串未扫描完时循环
switch (*postexp) {
case '+': {
Pop(sta, &a), Pop(sta, &b);
c=b+a;
Push(sta,c);//将计算结果c进栈
break;
}
case '-': {
Pop(sta, &a), Pop(sta, &b);
c=b-a;
Push(sta,c);
break;
}
case '*': {
Pop(sta, &a), Pop(sta, &b);
c=b*a;
Push(sta, c);
break;
}
case '/': {
Pop(sta, &a), Pop(sta, &b);
if (a!=0) {
c=b/a;
Push(sta, c);
break;
} else {
printf("\n\t除零错误!\n");
exit(0);//异常退出
}
break;
}
default: { //处理数字字符
d=0; //转换成对应的数值存放到d中
while (*postexp>='0' && *postexp<='9') {
d=10*d+*postexp-'0';
postexp++;
}
Push(sta, d);
break;
}
}
postexp++; //继续处理其他字符
}
GetTop(sta, &e); //取栈顶元素e
DestroyStack(sta); //销毁栈
return e; //返回e
}*/
int main() {
char exp[]="(56-20)/(4+2)";
char postexp[MaxSize];//="56#20#-4#2#+/";
trans(exp, postexp);
printf("中缀表达式:%s\n", exp);
printf("后缀表达式:%s\n", postexp);
//trans()\compvalue() 由于调用不同类型的栈,单个栈不能同时执行
// printf("表达式的值:%g\n", compvalue(postexp));
return 0;
}
走迷宫问题
【例】给定一个 M ×N的迷宫图、入口与出口、行走规则,求一条从指定入口到出口的路径。
所求路径必须是简单路径,即路径不重复。
行走规则:上、下、左、右相邻方块行走。其中(i,j)表示一个方块
- 参考程序(顺序栈)
#include <stdio.h>
#include <stdlib.h>
#define bool int
#define true 1
#define false 0
#define ElemType Box
#define MaxSize 10001
#define M 8
#define N 8
int mg[M+2][N+2]= {
{1, 1,1,1,1,1,1,1,1, 1},
{1, 0,0,1,0,0,0,1,0, 1},
{1, 0,0,1,0,0,0,1,0, 1},
{1, 0,0,0,0,1,1,0,0, 1},
{1, 0,1,1,1,0,0,0,0, 1},
{1, 0,0,0,1,0,0,0,0, 1},
{1, 0,1,0,0,0,1,0,0, 1},
{1, 0,1,1,1,0,1,1,0, 1},
{1, 1,0,0,0,0,0,0,0, 1},
{1, 1,1,1,1,1,1,1,1, 1}};
typedef struct {
int i; //当前方块的行号
int j; //当前方块的列号
int di; //di是下一可走相邻方位的方位号
} Box; //定义方块类型
typedef struct {
Box data[MaxSize];
int top; //栈顶指针
} SqStack; //定义顺序栈类型
//(1)初始化栈InitStack(s)
void InitStack(SqStack *s) {
s->top=-1;
}
//(2)销毁栈DestroyStack(s)
void DestroyStack(SqStack *s) {
free(s);
}
//(3)判断栈是否为空StackEmpty(s)
bool StackEmpty(SqStack *s) {
return(s->top==-1);
}
//(4)进栈Push(s,e)
bool Push(SqStack *s,ElemType e) {
if (s->top==MaxSize-1) { //栈满的情况,即栈上溢出
return false;
}
s->top++; //栈顶指针增1
s->data[s->top].i = e.i;
s->data[s->top].j = e.j;
s->data[s->top].di = e.di;
return true;
}
//(5)出栈Pop(s,e)
bool Pop(SqStack *s,ElemType *e) {
if (s->top==-1) { //栈为空的情况,即栈下溢出
return false;
}
*e=s->data[s->top]; //取栈顶指针元素的元素
s->top--; //栈顶指针减1
return true;
}
//(6)取栈顶元素GetTop(s,e)
bool GetTop(SqStack *s,ElemType *e) {
if (s->top==-1) { //栈为空的情况,即栈下溢出
return false;
}
*e = s->data[s->top]; //取栈顶指针元素的元素
return true;
}
bool mgpath(int xi,int yi,int xe,int ye) {
printf("sta_start: %d %d\n", xi, yi);
printf("sta_end : %d %d\n", xe, ye);
Box path[MaxSize], e;
int i,j,di,i1,j1,k;
bool find;
SqStack *sta=(SqStack*)malloc(sizeof(SqStack));
InitStack(sta); //初始化栈顶指针
e.i=xi, e.j=yi, e.di=-1; //设置e为入口
Push(sta,e); //方块e进栈
mg[xi][yi]=-1; //入口的迷宫值置为-1避免重复走到该方块
while (!StackEmpty(sta)) { //栈不空时循环
GetTop(sta, &e); //取栈顶方块e
i=e.i, j=e.j, di=e.di;
if (i==xe && j==ye) { //找到了出口,输出该路径
printf("一条迷宫路径如下:\n");
k=0;
while (!StackEmpty(sta)) {
Pop(sta, &e); //出栈方块e
path[k++]=e; //将e添加到path数组中
}
while (k>=1) {
k--;
printf("\t(%d,%d)",path[k].i,path[k].j);
if ((k+2)%5==0) { //每输出每5个方块后换一行
printf("\n");
}
}
printf("\n");
DestroyStack(sta); //销毁栈
return true; //输出一条迷宫路径后返回true
}
find=false;
while (di<4 && !find) { //找相邻可走方块(i1,j1)
di++;
switch(di) {
case 0: i1=i-1, j1=j; break;
case 1: i1=i, j1=j+1; break;
case 2: i1=i+1, j1=j; break;
case 3: i1=i, j1=j-1; break;
}
if (mg[i1][j1]==0) find=true; //找到一个相邻可走方块,设置find为真
}
if (find) { //找到了一个相邻可走方块(i1,j1)
sta->data[sta->top].di=di; //修改原栈顶元素的di值
e.i=i1, e.j=j1, e.di=-1;
Push(sta,e); //相邻可走方块e进栈
mg[i1][j1]=-1; //(i1,j1)迷宫值置为-1避免重复走到该方块
} else { //没有路径可走,则退栈
Pop(sta, &e); //将栈顶方块退栈
mg[e.i][e.j]=0; //让退栈方块的位置变为其他路径可走方块
}
// int ii=0,jj=0;
// for(ii=0; ii<M+2; ii++){ // 输出打印中间结果, 一个很好的debug方式
// for(jj=0; jj<N+2; jj++){
// printf("%d ", mg[ii][jj]);
// }printf("\n");
// }printf("\n\n");
}
DestroyStack(sta); //销毁栈
return false; //表示没有可走路径
}
int main() {
if(!mgpath(1,1,M,N)) {
printf("该迷宫问题没有解!");
}
return 1;
}
问题变化:给定一个 n*m 的矩阵,求重矩阵 左上角到 右下角的一条路径。
输入数据:
8 8
0 0 1 0 0 0 1 0
0 0 1 0 0 0 1 0
0 0 0 0 1 1 0 0
0 1 1 1 0 0 0 0
0 0 0 1 0 0 0 0
0 1 0 0 0 1 0 0
0 1 1 1 0 1 1 0
1 0 0 0 0 0 0 0
输出数据:
一条迷宫路径如下:
(1,1) (1,2) (2,2) (3,2) (3,1)
(4,1) (5,1) (5,2) (5,3) (6,3)
(6,4) (6,5) (5,5) (4,5) (4,6)
(4,7) (3,7) (3,8) (4,8) (5,8)
(6,8) (7,8) (8,8)
0 0 0 0 0 0 0 0 0 0
0 -1 -1 1 0 0 0 1 0 0
0 0 -1 1 0 0 0 1 0 0
0 -1 -1 0 0 1 1 -1 -1 0
0 -1 1 1 1 -1 -1 -1 -1 0
0 -1 -1 -1 1 -1 0 0 -1 0
0 0 1 -1 -1 -1 1 0 -1 0
0 0 1 1 1 0 1 1 -1 0
0 1 0 0 0 0 0 0 -1 0
0 0 0 0 0 0 0 0 0 0
- 参考程序(深度优先搜索)
#include<stdio.h>
#include<stdlib.h>
#define N 110
int a[N][N];
int dx[]={-1, 0, 1, 0};
int dy[]={ 0, 1, 0,-1};
int n,m,k=0;
struct T{
int x,y;
}path[N*N];
bool in(int x,int y){
if(x>=1&&x<=n&&y>=1&&y<=n) return 1;
return 0;
}
bool dfs(int x,int y){
a[x][y]=-1;
path[++k] = (T){x,y};
if(x==n&&y==m){
printf("一条迷宫路径如下:\n");
for(int i=1; i<=k; i++){
printf("\t(%d,%d)", path[i].x, path[i].y);
if(i%5==0) printf("\n");
}
printf("\n\n");
for(int i=0; i<n+2; i++){ // 打印,一个很好的debug方式
for(int j=0; j<m+2; j++){
printf("%3d ", a[i][j]);
}printf("\n");
}
exit(0); //正常退出
}
for(int i=0; i<4; i++){
int tx=x+dx[i];
int ty=y+dy[i];
if(in(tx,ty) && a[tx][ty]==0){
dfs(tx,ty);
a[tx][ty]=0, k--;
}
}
return false;
}
int main(){
freopen("data.in", "r", stdin);
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++){
for(int j=1; j<=m; j++){
scanf("%d", &a[i][j]);
}
}
if(!dfs(1,1)){
printf("该迷宫问题没有解!");
}
return 0;
}
这里很明显我们可以发现这样的方案结果不一定是最优解,那么如何才能得到最优解呢?
这里就需要使用广度优先搜索了, 而广度优先搜索又是基于队列的,所以需要先学习队列。
队列
队列简称队,它也是一种运算受限的线性表。
队列只能选取一个端点进行插入操作,另一个端点进行删除操作
把进行插入的一端称做队尾(rear)。
进行删除的一端称做队首或队头(front)。
向队列中插入新元素称为进队或入队,新元素进队后就成为新的队尾元素。
从队列中删除元素称为出队或离队,元素出队后,其后继元素就成为队首元素。
队列的主要特点是先进先出,所以又把队列称为先进先出表。
ADT Queue{
数据对象:D={ di | 0≤i≤n,n为一个正整数}
数据关系:无
基本运算:
Init(q) :初始化队列。构造一个空队列q。
Destroy(q) :销毁队列。释放队列q占用的存储空间。
Empty(q) :判断队列是否为空。若队列q为空,则返回真;否则返回假。
Push(q,e) :进队列。将元素e进队作为队尾元素。
Pop(q,e) :出队列。从队列q中出队一个元素,并将其值赋给e。
}
顺序队列
顺序队的4要素(初始时front=rear=-1):
队空条件 :front = rear
队满条件 :rear = MaxSize-1
元素e进队:rear++; data[rear]=e;
元素e出队:front++; e=data[front];
注意:rear指向队尾元素;front指向队头元素的前一个位置。
#include <stdio.h>
#include <stdlib.h>
#define bool int
#define true 1
#define false 0
#define ElemType int
#define MaxSize 10001
typedef struct {
ElemType data[MaxSize];
int front,rear; //队首和队尾指针
} SqQueue;
//(1)初始化队列
void Init(SqQueue *q) {
q->front=q->rear=-1;
}
//(2)销毁队列
void Destroy(SqQueue *q) {
free(q);
}
//(3)判断队列是否为空
bool Empty(SqQueue *q) {
return(q->front==q->rear);
}
//(4)进队列
bool Push(SqQueue *q,ElemType e) {
if (q->rear==MaxSize-1) {//队满上溢出
return false;
}
q->rear++;
q->data[q->rear]=e;
return true;
}
//(5)出队列
bool Pop(SqQueue *q,ElemType* e) {
if(q->front==q->rear) {//队空下溢出
return false;
}
q->front++;
*e=q->data[q->front];
return true;
}
int main() {
int a[]= {1,2,3,4,5,6};
int n = sizeof(a)/sizeof(int), i, e;
printf("n = %d\n", n);
SqQueue* que = (SqQueue*)malloc(sizeof(SqQueue));
Init(que);
for(i=0; i<n; i++) {
Push(que, a[i]);
}
while(!Empty(que)) {
Pop(que, &e);
printf("%d ", e);
}
Destroy(que);
return 0;
}
环形队列(或循环队列)
当队尾和队头指针都后移,且队尾指针已经指向最后一个队列位置的时候,发生队满情况,
但是这时候队首指针却并未指向队列的第一个位置,就会有一定的空间浪费。
这是因为采用rear==MaxSize-1作为队满条件的缺陷。
当队满条件为真时,队中可能还有若干空位置。
这种溢出并不是真正的溢出,称为假溢出。
解决方案:把数组的前端和后端连接起来,形成一个环形的顺序表,即把存储队列元素的表从逻辑上看成一个环,称为环形队列或循环队列。
实际上内存地址一定是连续的,不可能是环形的,这里是通过逻辑方式实现环形队列,
也就是将 rear++ 和 front++ 改为:
rear = (rear + 1) % MaxSize
front = (front + 1) % MaxSize
约定:rear = front 为队空条件,
(rear + 1) % MaxSize = front 为队满条件。
所以环形队列的四要素
队空条件 :front = rear
队满条件 :(rear+1)%MaxSize = front
进队e操作:rear=(rear+1)%MaxSize; 将e放在rear处
出队操作 :front=(front+1)%MaxSize; 取出front处元素e;
typedef struct {
ElemType data[MaxSize];
int front; //队头指针
int count; //队列中元素个数
} Queue;
void Init(Queue *q) { //初始化队运算算法
q->front = q->count = 0;
}
void Destroy(Queue *q) {
free(q);
}
bool Push(Queue *q, ElemType e) { //进队运算算法
int rear; //临时队尾指针
if (q->count==MaxSize) { //队满上溢出
return false;
} else {
rear=(q->front+q->count)%MaxSize;//求队尾位置
rear=(rear+1)%MaxSize; //队尾循环增1
q->data[rear]=e;
q->count++; //元素个数增1
return true;
}
}
bool Pop(Queue *q, ElemType *e) {//出队运算算法
if (q->count==0){ //队空下溢出
return false;
} else {
q->front=(q->front+1)%MaxSize;//队头循环增1
*e=q->data[q->front];
q->count--; //元素个数减1
return true;
}
}
bool Empty(Queue *q) { //判队空运算算法
return(q->count==0);
}
链队
采用链表存储的队列称为链队,这里采用不带头结点的单链表实现。
链队组成:
(1)存储队列元素的单链表结点
(2) 指向队头和队尾指针的链队头结点
#include <stdio.h>
#include <stdlib.h>
#define bool int
#define true 1
#define false 0
#define ElemType int
#define MaxSize 10001
typedef struct qnode {
ElemType data; //数据元素
struct qnode *next;
} DataNode;
typedef struct {
DataNode *front; //指向单链表队头结点
DataNode *rear; //指向单链表队尾结点
} LinkQuNode;
//(1)初始化队列
void Init(LinkQuNode *q) {
// q=(LinkQuNode *)malloc(sizeof(LinkQuNode));
q->front=q->rear=NULL;
}
// (2)销毁队列
void Destroy(LinkQuNode *q) {
DataNode *p=q->front, *r; //p指向队头数据结点
if (p!=NULL) { //释放数据结点占用空间
r=p->next;
while (r!=NULL) {
free(p);
p=r;
r=p->next;
}
}
free(p);
free(q); //释放链队结点占用空间
}
//(3)判断队列是否为空
bool Empty(LinkQuNode *q) {
return(q->rear==NULL);
}
//(4) 进队
void Push(LinkQuNode *q, ElemType e) {
DataNode *p;
p=(DataNode *)malloc(sizeof(DataNode));
p->data=e;
p->next=NULL;
if (q->rear==NULL) { //若链队为空,新结点是队首结点又是队尾结点
q->front=q->rear=p;
} else {
q->rear->next=p; //将p结点链到队尾,并将rear指向它
q->rear=p;
}
}
//(5)出队
bool Pop(LinkQuNode *q, ElemType *e) {
if(q->rear==NULL) return false; //队列为空
DataNode *t=q->front; //t指向第一个数据结点
if (q->front==q->rear){ //队列中只有一个结点时
q->front=q->rear=NULL;
} else { //队列中有多个结点时
q->front=q->front->next;
}
*e=t->data;
free(t);
return true;
}
int main() {
int a[]= {1,2,3,4,5,6};
int n = sizeof(a)/sizeof(int), i, e;
printf("n = %d\n", n);
LinkQuNode* que = (LinkQuNode*)malloc(sizeof(LinkQuNode));
Init(que);
for(i=0; i<n; i++) {
Push(que, a[i]);
}
while(!Empty(que)) {
Pop(que, &e);
printf("%d ", e);
}
Destroy(que);
return 0;
}
迷宫问题
问题变化:给定一个 n*m 的矩阵,求重矩阵 左上角到 右下角的一条路径。
输入数据:
8 8
0 0 1 0 0 0 1 0
0 0 1 0 0 0 1 0
0 0 0 0 1 1 0 0
0 1 1 1 0 0 0 0
0 0 0 1 0 0 0 0
0 1 0 0 0 1 0 0
0 1 1 1 0 1 1 0
1 0 0 0 0 0 0 0
输出数据:
一条迷宫路径如下:
(1, 1) (2, 1) (3, 1) (4, 1) (5, 1)
(5, 2) (5, 3) (6, 3) (6, 4) (6, 5)
(7, 5) (8, 5) (8, 6) (8, 7) (8, 8)
1 2 1 8 9 10 1 0
2 3 1 7 8 9 1 0
3 4 5 6 1 1 15 0
4 1 1 1 12 13 14 15
5 6 7 1 11 12 13 14
6 1 8 9 10 1 14 15
7 1 1 1 11 1 1 0
1 0 14 13 12 13 14 15
- 参考程序(广度优先搜索:一般用于求最短路径)
#include<stdio.h>
#include<stdlib.h>
#define N 110
int a[N][N];
int dx[]= {-1, 0, 1, 0};
int dy[]= { 0, 1, 0,-1};
int n,m,k=0;
struct T {
int x, y, pre;
} path[N*N], que[N*N];
bool in(int x,int y) {
if(x>=1&&x<=n&&y>=1&&y<=n) return 1;
return 0;
}
void pr(T temp) {
static int cnt=0;//静态局部,作用域结束,但不销毁,下次继续用
if(temp.pre==-1) {
printf("\t(%d, %d) ", temp.x, temp.y);
cnt++;
return;
}
pr(que[temp.pre]);
printf("\t(%d, %d) ", temp.x, temp.y);
cnt++;
if(cnt%5==0) printf("\n");
}
void pr2() {
int i=0,j=0;
printf("\n");
for(i=1; i<=n; i++) { // 输出打印中间结果, 一个很好的debug方式
for(j=1; j<=m; j++) {
printf("%3d ", a[i][j]);
}
printf("\n");
}
printf("\n\n");
}
bool bfs(int x,int y) {
int front=0, rear=-1, pre=-1;
T t; t.x=x, t.y=y, t.pre=-1;
que[++rear]=t; a[x][y]=1;
while(front <= rear) {
T temp = que[front];
for(int i=0; i<4; i++) {
int tx = temp.x + dx[i];
int ty = temp.y + dy[i];
if(in(tx,ty) && a[tx][ty]==0) {
T temp2;
temp2.x=tx, temp2.y=ty, temp2.pre=front;
que[++rear] = temp2;
a[tx][ty] = a[temp.x][temp.y]+1;
if(tx==n && ty==m) {
printf("一条迷宫路径如下:\n");
pr(que[rear]);
pr2(); //打印输出全局
return 1;
}
}
}
++front;
}
return false;
}
int main() {
freopen("data.in", "r", stdin);
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) {
for(int j=1; j<=m; j++) {
scanf("%d", &a[i][j]);
}
}
if(!bfs(1,1)) {
printf("该迷宫问题没有解!");
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号