chapter_2 线性表
1. 自定义一个抽象数据类型
描述一个集合的抽象数据类型Set,其中所有元素为正整数,集合的基本运算包括:
(1)由整数数组a[0..n-1]创建一个集合。
(2)输出一个集合的所有元素。
(3)判断一个元素是否在一个集合中。
(4)求两个集合的并集。
(5)求两个集合的差集。
(6)求两个集合的交集。
在此基础上设计集合的顺序存储结构,并实现各基本运算的算法。
ADT Set {
数据对象:D={ di | 0≤i≤n,n为一个正整数}
数据关系:无。
基本运算:
createset(s,a,n):创建一个集合s;
dispset(s):输出集合s;
inset(s,e):判断e是否在集合s中
void add(s1,s2,s3):s3=s1∪s2; //求集合的并集
void sub(s1,s2,s3):s3=s1-s2; //求集合的差集
void intersection(s1,s2,s3):s3=s1∩s2; //求集合的交集
}
【参考程序】该数据类型原理上是一个顺序表的实现
#include<stdio.h>
#define bool int
#define true 1
#define false 0
#define MaxSize 10001
typedef struct { //集合结构体类型
int data[MaxSize]; //存放集合中的元素,其中MaxSize为常量
int length; //存放集合中实际元素个数
} Set; //将集合结构体类型用一个新类型名Set表示
void createset(Set* s,int a[],int n) { //创建一个集合
int i;
for (i=0; i<n; i++) {
s->data[i]=a[i];
}
s->length=n;
}
void dispset(Set s) { //输出一个集合
int i;
for (i=0; i<s.length; i++) {
printf("%d ",s.data[i]);
}
printf("\n");
}
bool inset(Set s,int e) { //判断e是否在集合s中
int i;
for (i=0; i<s.length; i++) {
if (s.data[i]==e) {
return true;
}
}
return false;
}
void add(Set s1,Set s2,Set* s3) { //求集合的并集
int i;
for (i=0; i<s1.length; i++) { //将集合s1的所有元素复制到s3中
s3->data[i]=s1.data[i];
}
s3->length=s1.length;
for (i=0; i<s2.length; i++) { //将s2中不在s1中出现的元素复制到s3中
if (!inset(s1,s2.data[i])) {
s3->data[s3->length]=s2.data[i];
s3->length++;
}
}
}
void sub(Set s1,Set s2,Set* s3) { //求集合的差集
int i;
s3->length=0;
for (i=0; i<s1.length; i++) { //将s1中不出现在s2中的元素复制到s3中
if (!inset(s2, s1.data[i])) {
s3->data[s3->length]=s1.data[i];
s3->length++;
}
}
}
void intersection(Set s1,Set s2,Set* s3) { //求集合的交集
int i;
s3->length=0;
for (i=0; i<s1.length; i++) {//将s1中出现在s2中的元素复制到s3中
if (inset(s2,s1.data[i])) {
s3->data[s3->length]=s1.data[i];
s3->length++;
}
}
}
int main() {
Set s1,s2,s3,s4,s5;
int a[]= {1,2,3,4,5};
int b[]= {2,3,4,5,6,7,8};
int n=5,m=7;
createset(&s1,a,n);
createset(&s2,b,m);
printf("s1:");
dispset(s1);
printf("s2:");
dispset(s2);
printf("s3=s1∪s2\n");
add(s1,s2,&s3);
printf("s3:");
dispset(s3);
printf("s4=s1-s2\n");
sub(s1,s2,&s4);
printf("s4:");
dispset(s4);
printf("s5=s1∩s2\n");
intersection(s1,s2,&s5);
printf("s5:");
dispset(s5);
return 0;
}
线性表是一个具有相同特性的数据元素的有限序列。
相同特性:所有元素属于同一数据类型。
有限:数据元素个数是有限的。
序列:数据元素由逻辑序号唯一确定。一个线性表中可以有相同值的元素。
线性表中所含元素的个数叫做线性表的长度,用n表示,n≥0。
n=0时,表示线性表是一个空表,即表中不包含任何元素。
线性表的逻辑表示为:(a1,a2,…,ai,ai+1,…,an)
ai(1≤i≤n)表示第i(i表示逻辑位序)个元素。
a1为表头元素, an为表尾元素
ADT List{
数据对象:D={ di | 0≤i≤n,n为一个正整数}
数据关系:无
基本运算:
InitList(L):初始化线性表,构造一个空的线性表L。
DestroyList(L):销毁线性表,释放线性表L占用的内存空间。
ListEmpty(L):判线性表是否为空表,若L为空表,则返回真,否则返回假。
ListLength(L):求线性表的长度,返回L中元素个数n。
DispList(L):输出线性表,线性表L不为空时,顺序显示L中各结点的值域。
GetElem(L,i,e):求线性表L中指定位置的某个数据元素,用e返回L中第 i(1≤i≤n)个元素的值。
LocateElem(L,e):定位查找,返回L中第一个值域与e相等的逻辑位序。若这样的元素不存在,则返回值为0。
ListInsert(L,i,e):插入一个数据元素,在L的第i(1≤i≤n)个元素之前插入新的元素e,L的长度增1。
ListDelete(L,i,e):删除数据元素,删除L的第i(1≤i≤n)个元素,并用e返回其值,L的长度减1。
}
2. 线性表的顺序存储—顺序表
线性表的顺序存储结构:把线性表中的所有元素按照顺序存储方法进行存储。
按逻辑顺序依次存储到存储器中一片连续的存储空间中。
#include <stdio.h>
#include <stdlib.h>
#define bool int
#define true 1
#define false 0
#define ElemType char
#define MaxSize 10001
typedef struct {
ElemType data[MaxSize];
int length;
} SqList;
//整体建立顺序表
void CreateList(SqList* L, ElemType a[], int n) {
int i = 0, k = 0;
while (i < n) {
L->data[k] = a[i]; // i扫描a中元素
k++;
i++; // k记录插入到L中的元素个数
}
L->length = k;
}
//(1)初始化线性表InitList(L)
void InitList(SqList* L) {
L = (SqList *)malloc(sizeof(SqList));
L->length = 0;
}
//(2)销毁线性表DestroyList(L)
void DestroyList(SqList* L) {
free(L);
}
//(3)判定是否为空表ListEmpty(L)
bool ListEmpty(SqList* L) {
return (L->length == 0);
}
//(4)求线性表的长度ListLength(L)
int ListLength(SqList* L) {
return (L->length);
}
//(5)输出线性表DispList(L)
void DispList(SqList* L) {
int i;
if (ListEmpty(L)) {
return;
}
printf("length: %d\n", L->length);
printf("data: ");
for (i = 0; i < L->length; i++) {
printf("%c", L->data[i]);
}
printf("\n");
}
//(6)求线性表L中指定位置的某个数据元素GetElem(L,i,&e)
bool GetElem(SqList* L, int i, ElemType* e) {
if (i < 1 || i > L->length) {
return false;
}
*e = L->data[i - 1];
return true;
}
//(7)按元素值查找LocateElem(L,e)
int LocateElem(SqList* L, ElemType e) {
int i = 0;
while (i < L->length && L->data[i] != e) {
i++;
}
if (i >= L->length) {
return 0;
} else {
return i + 1;
}
}
//(8)插入数据元素ListInsert(L,i,e)
bool ListInsert(SqList* L, int i, ElemType e) {
int j;
if (i < 1 || i > L->length + 1) {
return false; //参数错误时返回false
}
i--; //将顺序表逻辑序号转化为物理序号
for (j = L->length; j > i; j--) { //将data[i..n]元素后移一个位置
L->data[j] = L->data[j - 1];
}
L->data[i] = e; //插入元素e
L->length++; //顺序表长度增1
return true; //成功插入返回true
}
//(9)删除数据元素第i个元素,并存入e: ListDelete(L,i,e)
bool ListDelete(SqList* L, int i, ElemType* e) {
int j;
if (i < 1 || i > L->length) { //参数错误时返回false
return false;
}
i--; //将顺序表逻辑序号转化为物理序号
*e = L->data[i];
for (j = i; j < L->length - 1; j++) { //将data[i..n-1]元素前移
L->data[j] = L->data[j + 1];
}
L->length--; //顺序表长度减1
return true; //成功删除返回true
}
int main() {
char a[] = "abcdef";
int n = sizeof(a) / sizeof(a[0]) - 1; // '\0'
SqList* L = (SqList *)malloc(sizeof(SqList));
CreateList(L, a, n);
DispList(L);
char e;
GetElem(L, 1, &e);
printf("e = %c\n", e);
int index = LocateElem(L, e);
printf("index = %d\n", index);
ListInsert(L, 1, e);
DispList(L);
ListDelete(L, 1, &e);
printf("e = %c\n", e);
DispList(L);
return 0;
}
【例】已知长度为 n 的线性表 L 采用顺序存储结构。
设计一个时间复杂度为 O(n)、空间复杂度为 O(1) 的算法,
该算法删除线性表中所有值为 e 的数据元素。
解法一(重建法):设删除 L 中所有值等于 e 元素后的顺序表为 L1,
显然 L1 包含在 L 中,为此 L1 重用 L 的空间。
思路:扫描顺序表 L,重建 L 只包含不等于 x 的元素。
void delnode1(SqList* L, ElemType e) {
int k = 0, i; // k记录值不等于e的元素个数
for (i = 0; i < L->length; i++){
if (L->data[i] != e) {
L->data[k] = L->data[i];
k++; //不等于e的元素增1
}
}
L->length = k; //顺序表L的长度等于k
}
解法二(前移法):用 k 记录顺序表 L 中等于 e 的元素个数,一边扫描 L 一边统计 k 值。
思路:将不为 e 的元素前移 k 个位置,最后修改 L 的长度。
void delnode2(SqList* L,ElemType e) {
int k = 0, i = 0; // k记录值等于x的元素个数
while (i < L->length) {
if (L->data[i] == e){ //当前元素值为x时k增1
k++;
}else{ //当前元素不为x时将其前移k个位置
L->data[i - k] = L->data[i];
}
i++;
}
L->length -= k; //顺序表L的长度递减k
}
解法三(区间划分法)
void delnode3(SqList* L, ElemType e) {
int i = -1,j = 0;
ElemType temp;
while (j < L->length) { // j扫描所有元素
if (L->data[j] != e) { //找到不为x的元素
i++; //扩大不为x的区间
if (i != j){
temp=L->data[i];
L->data[i] = L->data[j];
L->data[j] = temp;
}
}
j++; //继续扫描
}
L->length = i + 1; //设置L中实际元素个数
}
【例】设顺序表L有10个整数。 设计一个算法,以第一个元素为分界线(基准),
将所有小于等于它的元素移到该元素的前面,
将所有大于它的元素移到该元素的后面。
解法1(前后交换法):
void move1(SqList* L) {
int i = 0, j = L->length - 1;
ElemType temp;
ElemType pivot = L->data[0]; //以data[0]为基准
while (i < j) {
while (i < j && L->data[j] > pivot){
j--; //从后向前扫描,找一个≤pivot的元素
}
while (i < j && L->data[i] <= pivot){
i++; //从前向后扫描,找一个>pivot的元素
}
if (i < j) {
temp = L->data[i]; // L->data[i] ? L->data[j]
L->data[i] = L->data[j];
L->data[j] = temp;
}
}
temp = L->data[0]; // L->data[0] ? L->data[j]
L->data[0] = L->data[j];
L->data[j] = temp;
}
解法2 (前后交换法) :
void move2(SqList* L) {
int i = 0,j = L->length - 1;
ElemType pivot = L->data[0]; //以data[0]为基准
while (i < j) {
while (j > i && L->data[j] > pivot){
j--; //从右向左扫描,找≤pivot的data[j]
}
L->data[i] = L->data[j]; //将其放入data[i]处
while (i < j && L->data[i] <= pivot){
i++; //从左向右扫描,找>pivot的记录data[i]
}
L->data[j] = L->data[i]; //将其放入data[j]处
}
L->data[i] = pivot; //放置基准
}
3. 线性表的链式存储—单链表
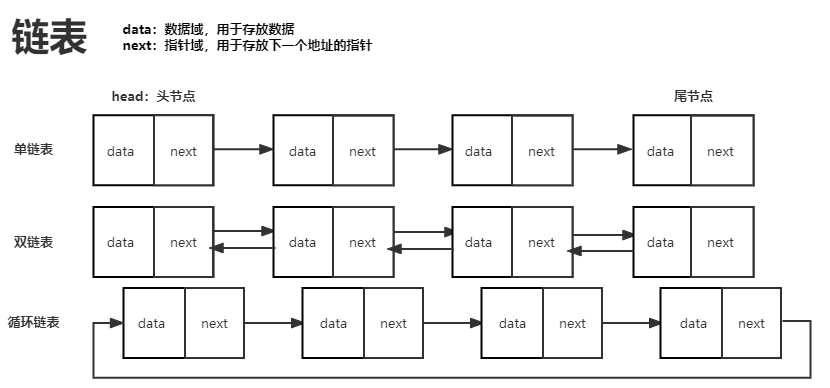
线性表中每个结点有唯一的前驱结点和前驱结点。
设计链式存储结构时,每个逻辑结点存储单独存储,为了表示逻辑关系,增加指针域。
每个物理结点增加一个指向后继结点的指针域 -> 单链表。
每个物理结点增加一个指向后继结点的指针域和一个指向前驱结点的指针域 -> 双链表。
第一个结点的操作和表中其他结点的操作相一致,无需进行特殊处理;
无论链表是否为空,都有一个头结点,因此空表和非空表的处理也就统一了。
#include <stdio.h>
#include <stdlib.h>
#define bool int
#define true 1
#define false 0
#define ElemType char
#define MaxSize 10001
typedef struct LNode {
ElemType data;
struct LNode *next; //指向后继结点
} LinkNode; //定义单链表结点类型
//(1)头插法建表
void CreateListF(LinkNode* L, ElemType a[], int n) {
LinkNode *s;
int i;
L->next = NULL; //头结点next域置为NULL
for (i = 0; i < n; i++) {
//循环建立数据结点
s = (LinkNode *)malloc(sizeof(LinkNode));
s->data = a[i]; //创建数据结点s
s->next = L->next; //将s插在原开始结点之前,头结点之后
L->next = s;
}
}
//(2)尾插法建表
void CreateListR(LinkNode* L, ElemType a[], int n) {
LinkNode *s, *r;
int i;
r = L; // r始终指向尾结点,开始时指向头结点
for (i = 0; i < n; i++) {
s = (LinkNode *)malloc(sizeof(LinkNode));
s->data = a[i]; //创建数据结点s
r->next = s; //将s插入r之后
r = s;
}
r->next = NULL; //尾结点next域置为NULL
}
//(1)初始化线性表InitList(L)
void InitList(LinkNode* L) {
L = (LinkNode *)malloc(sizeof(LinkNode)); //创建头结点
L->next = NULL;
}
//(2)销毁线性表DestroyList(L)
void DestroyList(LinkNode* L) {
LinkNode *pre = L, *p = L->next; // pre指向p的前驱结点
while (p != NULL) {
//扫描单链表L
free(pre); //释放pre结点
pre = p; // pre、p同步后移一个结点
p = pre->next;
}
free(pre); //循环结束时,p为NULL,pre指向尾结点,释放它
}
//(3)判线性表是否为空表ListEmpty(L)
bool ListEmpty(LinkNode* L) {
return (L->next == NULL);
}
//(4)求线性表的长度ListLength(L)
int ListLength(LinkNode* L) {
int n = 0;
LinkNode *p = L; // p指向头结点,n置为0(即头结点的序号为0)
while (p->next != NULL) {
n++;
p = p->next;
}
return (n); //循环结束,p指向尾结点,其序号n为结点个数
}
//(5)输出线性表DispList(L)
void DispList(LinkNode* L) {
LinkNode *p = L->next;
printf("data: ");
while (p != NULL) {
printf("%c", p->data);
p = p->next;
}
printf("\n");
}
//(6)求线性表L中位置i的数据元素GetElem(L,i,e)
bool GetElem(LinkNode* L, int i, ElemType* e) {
int j = 0;
LinkNode *p = L; // p指向头结点,j置为0(即头结点的序号为0)
while (j < i && p != NULL) {
j++;
p = p->next;
}
if (p == NULL) {
return false; //不存在第i个数据结点,返回false
} else {
//存在第i个数据结点,返回true
*e = p->data;
return true;
}
}
//(7)按元素值查找LocateElem(L,e)
int LocateElem(LinkNode* L, ElemType e) {
int i = 1;
LinkNode *p = L->next; // p指向开始结点,i置为1
while (p != NULL && p->data != e) {
p = p->next; //查找data值为e的结点,其序号为i
i++;
}
if (p == NULL) {
return 0; //不存在元素值为e的结点,返回0
} else {
return i; //存在元素值为e的结点,返回其逻辑序号i
}
}
//(8)插入数据元素ListInsert(L,i,e)
bool ListInsert(LinkNode* L, int i, ElemType e) {
int j = 0;
LinkNode *p = L, *s; // p指向头结点,j置为0
while (j < i - 1 && p != NULL) {
j++;
p = p->next;
}
if (p == NULL) {
return false; //未找到第i-1个结点,返回false
} else {
//找到第i-1个结点p,插入新结点并返回true
s = (LinkNode *)malloc(sizeof(LinkNode));
s->data = e; //创建新结点s,其data域置为e
s->next = p->next; //将s插入到p之后
p->next = s;
return true;
}
}
//(9)删除数据元素ListDelete(L,i,e)
bool ListDelete(LinkNode* L, int i, ElemType* e) {
int j = 0;
LinkNode *p = L, *q; // p指向头结点,j置为0
while (j < i - 1 && p != NULL) {
//查找第i-1个结点
j++;
p = p->next;
}
if (p == NULL) {
return false; //未找到第i-1个结点,返回false
} else {
//找到第i-1个结点p
q = p->next; // q指向第i个结点
if (q == NULL) {
*e = q->data; //若不存在第i个结点,返回false
}
p->next = q->next; //从单链表中删除q结点
free(q); //释放q结点
return true; //返回true表示成功删除第i个结点
}
}
int main() {
char a[] = "abcdef";
int n = sizeof(a) / sizeof(a[0]) - 1; // '\0'
LinkNode *L = (LinkNode *)malloc(sizeof(LinkNode));
CreateListF(L, a, n);
DispList(L);
CreateListR(L, a, n);
DispList(L);
char e;
GetElem(L, 1, &e);
printf("e = %c\n", e);
int index = LocateElem(L, e);
printf("index = %d\n", index);
ListInsert(L, 1, e);
DispList(L);
ListDelete(L, 3, &e);
DispList(L);
return 0;
}
【例】设计一个算法,删除一个单链表L中元素值最大的结点(假设最大值结点是唯一的)。
void delmaxnode(LinkNode* L) {
LinkNode *p = L->next, *pre = L, *maxp = p, *maxpre = pre;
while (p != NULL) {
if (maxp->data < p->data) { //若找到一个更大的结点
maxp = p; //更改maxp
maxpre = pre; //更改maxpre
}
pre = p; // p、pre同步后移一个结点
p = p->next;
}
maxpre->next = maxp->next; //删除maxp结点
free(maxp); //释放maxp结点
}
【例】有一个带头结点的单链表L(至少有一个数据结点),
设计一个算法使其元素递增有序排列。
void sort(LinkNode* L) {
LinkNode *p, *pre, *q;
p = L->next->next; // p指向L的第2个数据结点
L->next->next = NULL; //构造只含一个数据结点的有序表
while (p != NULL) {
q = p->next; // q保存p结点后继结点的指针
pre = L; //从有序表开头进行比较,pre指向插入p的前驱结点
while (pre->next != NULL && pre->next->data < p->data){
pre = pre->next; //在有序表中找插入p的前驱结点pre
}
p->next = pre->next;
pre->next = p;
p = q; //扫描原单链表余下的结点
}
}
【例】 假设有一个带头结点的单链表:L = (a1,a2,…,an)。
设计一个算法将所有结点逆置,即:L = (an,an - 1,…,a1)
void Reverse(LinkNode* L) {
LinkNode *p = L->next, * q;
L->next = NULL;
while (p != NULL) {
q = p->next; //临时保存p的后继结点
p->next = L->next; //将p结点采用头插法连接
L->next = p;
p = q;
}
}
【例】假设有一个带头结点的单链表 L = (a1,b1,a2,b2,…,an,bn)。
设计一个算法将其拆分成两个带头结点的单链表L1和L2:
L1 = (a1,a2,…,an), L2 = (bn,bn - 1,…,b1)
要求L1使用L的头结点。
解:利用原单链表L中的所有结点通过改变指针域重组成单链表L1和L2。
由于L1中结点的相对顺序与L中的相同,所以采用尾插法建立单链表L1;
由于L2中结点的相对顺序与L中的相反,所以采用头插法建立单链表L2。
void split(LinkNode* L, LinkNode* L1, LinkNode* L2) {
LinkNode *p = L->next, * q, * r1; // p指向第1个数据结点
L1 = L; // L1利用原来L的头结点
r1 = L1; // r1始终指向L1的尾结点
L2 = (LinkNode *)malloc(sizeof(LinkNode)); //创建L2的头结点
L2->next = NULL; //置L2的指针域为NULL
while (p != NULL) {
r1->next = p; //采用尾插法将p(data值为ai)插入L1中
r1 = p;
p = p->next; // p移向下一个结点(data值为bi)
q = p->next; //用q保存p的后继结点
p->next = L2->next; //采用头插法将p插入L2中
L2->next = p;
p = q; // p重新指向ai+1的结点
}
r1->next = NULL; //尾结点next置空
}
4. 双链表
#include <stdio.h>
#include <stdlib.h>
#define bool int
#define true 1
#define false 0
#define ElemType int
#define MaxSize 10001
typedef struct DNode { //双链表结点类型
ElemType data;
struct DNode *prior; //指向前驱结点
struct DNode *next; //指向后继结点
} DLinkNode;
//头插法建立双链表:由含有n个元素的数组a创建带头结点的双链表L。
void CreateListF(DLinkNode *L,ElemType a[] ,int n) {
DLinkNode *s;
int i;
L->prior = L->next = NULL; //前后指针域置为NULL
for (i = 0; i < n; i++) { //循环建立数据结点
s = (DLinkNode *)malloc(sizeof(DLinkNode));
s->data = a[i]; //创建数据结点s
s->next = L->next; //将s插入到头结点之后
if (L->next != NULL){ //若L存在数据结点,修改前驱指针
L->next->prior = s;
}
L->next = s;
s->prior = L;
}
}
//尾插法建立双链表:由含有n个元素的数组a创建带头结点的双链表L。
void CreateListR(DLinkNode *L,ElemType a[] ,int n) {
DLinkNode *s, *r;
int i;
L->prior = L->next = NULL; //前后指针域置为NULL
r = L; // r始终指向尾结点,开始时指向头结点
for (i = 0; i < n; i++) { //循环建立数据结点
s = (DLinkNode *)malloc(sizeof(DLinkNode));
s->data = a[i]; //创建数据结点s
r->next = s;
s->prior = r; //将s插入r之后
r = s; // r指向尾结点
}
r->next = NULL; //尾结点next域置为NULL
}
//输出线性表DispList(L)
void DispList(DLinkNode* L) {
DLinkNode *p = L->next;
printf("data: ");
while (p != NULL) {
printf("%d ", p->data);
p = p->next;
}
printf("\n");
}
//双链表的插入算法
bool ListInsert(DLinkNode *L,int i,ElemType e) {
int j = 0;
DLinkNode *p = L, * s; // p指向头结点,j设置为0
while (j < i - 1 && p != NULL) { //查找第i-1个结点
j++;
p = p->next;
}
if (p == NULL) return false;//未找到第i-1个结点,返回false
else { //找到第i-1个结点p,在其后插入新结点s
s = (DLinkNode *)malloc(sizeof(DLinkNode));
s->data = e; //创建新结点s
s->next = p->next; //在p之后插入s结点
if (p->next != NULL) p->next->prior = s;//若存在后继结点,修改其前驱指针
s->prior = p;
p->next = s;
return true;
}
}
//双链表的删除算法
bool ListDelete(DLinkNode *L,int i,ElemType *e) {
int j = 0;
DLinkNode *p = L, * q; // p指向头结点,j设置为0
while (j < i - 1 && p != NULL) { //查找第i-1个结点
j++;
p = p->next;
}
if (p == NULL) return false;//未找到第i-1个结点
else { //找到第i-1个结点p
q = p->next; // q指向第i个结点
if (q == NULL) return false;//当不存在第i个结点时返回false
*e = q->data;
p->next = q->next; //从双单链表中删除q结点
if (p->next != NULL) p->next->prior = p;//修改其前驱指针
free(q); //释放q结点
return true;
}
}
//逆置
void Reverse(DLinkNode *L) { //双链表结点逆置
DLinkNode *p = L->next, * q; // p指向开始结点
L->next = NULL; //构造只有头结点的双链表L
while (p != NULL) { //扫描L的数据结点
q = p->next; //用q保存其后继结点
p->next = L->next; //采用头插法将p结点插入
if (L->next != NULL) L->next->prior = p;//修改其前驱指针
L->next = p;
p->prior = L;
p = q; //让p重新指向其后继结点
}
}
//输出线性表DispList(L)
void DispList2(DLinkNode* L) {
DLinkNode *p = L->next;
printf("data: ");
while (p->next != NULL) {
p = p->next;
}
while(p->prior!=NULL){
printf("%d ", p->data);
p = p->prior;
}
printf("\n");
}
int main() {
int a[] = {1, 2, 3, 4, 5, 6};
int n = sizeof(a) / sizeof(int);
DLinkNode *L=(DLinkNode *)malloc(sizeof(DLinkNode));
CreateListF(L, a, n);
// CreateListR(L, a, n);
DispList(L);
DispList2(L);
Reverse(L);
DispList(L);
return 0;
}
5. 循环链表
对于链表新增一个头尾相连的特性而已。
tail->next = head;
6. 些许建议
本质上所有的数据结构都是数据以及对于数据的些许操作的集合,有不同的实现方式,我们在数据结构的这门课程中更多的是使用单个结点,通过指针指向下一个结点来实现,这样能够使得存储空间不连续,在某种意义上可以建立一个长度极大的链表。
但是如果对于算法而言,这样的实现方式过于复杂和不实用,所以我们经常会采用数组的方式来实现,不过这样需要占用连续的内存空间,有一定的限制。
笔者建议:根据不同的情况具体分析,发现两种方式都需要掌握,O(∩_∩)O哈哈~。
但是对于竞赛,利用数组实现更为常见。
如果各位看官看到此处,那么我有几个小问题提出:
- 对于上述知识的理论逻辑是否已经掌握?
- 对于上诉程序代码自己是否已经自己实现过?
- 如果给你一份魔改之后的链表程序,是否可以看懂,并且做出合适的修改,使得程序更为优美?
如果上述几点你都已经做到,那么恭喜你,这个知识你已经完全掌握,并且具备自学后续数据结构的能力了。
如果你只是做到了第1点,那么请务必完成后面几点,因为很多事情都是 "说着容易,做着难",你不去实现一下这个程序,你完全不知道里面有哪些不知名的坑在等着你。
我们需要掌握理论,但同时也需要具备将理论实现的能力。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号