码[简单总结，待完善]

目录

• 原码
  • 整数：
    • 表示方法：
    • 示例（8位）：
    • 特点：
    • 范围（n位整数）：
  • 小数：
    • 1. 原码小数的结构
    • 2. 最大正小数的推导
    • 3. 最小负小数的推导
    • 4. 表示范围总结
    • 关键点：
• 反码
• 补码
• 移码
• 移码的编码规则
  • • 移码的转换示例

原码

整数：

表示方法：

• 符号位：最高位（0=正，1=负）
• 数值位：剩余位表示绝对值

示例（8位）：

• +5 → 00000101
• -5 → 10000101

特点：

• 直观，但存在 +0（00000000）和 -0（10000000）
• 加减运算复杂，需单独处理符号位

范围（n位整数）：

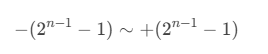
小数：

===================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================

1. 原码小数的结构

• 1位符号位（最高位）：0表示正，1表示负。
• n-1位数值位：表示小数的绝对值，小数点固定在符号位之后。

格式：

[符号位] . [数值位]

例如，8位原码小数：

• 符号位：第1位
• 数值位：后7位（小数点隐含在符号位后）

---

2. 最大正小数的推导

（符号位=0，数值位全1）

• 数值位的最大值：所有位为 1，即：

  数值=∑i=1n−12−i=1−2−(n−1)数值=i=1∑n−12−i=1−2−(n−1)

• 举例（n=8）：

  • 数值位 1111111：

    0.11111112=12+14+⋯+1128=1−1128=0.9921875100.11111112=21+41+⋯+1281=1−1281=0.992187510

  • 最大正小数：+0.9921875。

---

3. 最小负小数的推导

（符号位=1，数值位全1）

• 绝对值与最大正小数相同，但符号为负：

  最小值=−(1−2−(n−1))最小值=−(1−2−(n−1))

• 举例（n=8）：

  • 最小负小数：-0.9921875。

---

4. 表示范围总结

对于 n位原码小数：

范围=[−(1−2−(n−1)), +(1−2−(n−1))]范围=[−(1−2−(n−1)), +(1−2−(n−1))]

或写作：

−(1−2−(n−1))≤x≤+(1−2−(n−1))−(1−2−(n−1))≤x≤+(1−2−(n−1))

关键点：

1. 无法表示 ±1.0：因为数值位全1时，值为 1−2−(n−1)1−2−(n−1)，无法达到 1.0。
2. 零的表示：原码有 +0（0 000...0）和 -0（1 000...0）两种形式。

反码

补码

移码

移码值=真值+K

移码的编码规则

真值	移码计算（K=128）	8位二进制
+127	127 + 128 = 255	11111111
+1	1 + 128 = 129	10000001
0	0 + 128 = 128	10000000
-1	-1 + 128 = 127	01111111
-128	-128 + 128 = 0	00000000

移码的转换示例

示例1：将真值 -25 转换为8位移码（K=128）

1. 计算移码值：-25 + 128 = 103
2. 二进制表示：01100111

示例2：从移码 10110100（K=128）恢复真值

1. 十进制值：180
2. 真值：180 - 128 = 52