寻路算法

目录

• 寻路算法
  • 核心区别：代价函数的定义
    • 1. Dijkstra 算法：严谨的实干家
    • 2. GBFS 算法：贪婪的冒险家
    • 直观比喻
    • 总结与关系
  • 寻路算法核心特性对比总表
  • 详细分解
    • 1. 广度优先搜索（BFS）
    • 2. 深度优先搜索（DFS）
    • 3. Dijkstra 算法
    • 4. 贪心最佳优先搜索（GBFS）
    • 5. A*（A-Star）算法
  • 直观图示与总结
  • 简单画图示意
    • BFS
    • DFS
    • Dijkstra
    • GBFS
    • A*
  • 可参考：

寻路算法

核心区别：代价函数的定义

理解它们关系的关键在于看它们决定下一步探索哪个节点时，所使用的代价函数。

算法	代价函数	含义
Dijkstra	f(n) = g(n)	g(n): 从起点到当前节点 n 的实际代价。只关心已经发生的历史成本。
GBFS	f(n) = h(n)	h(n): 从当前节点 n 到终点的估计代价（启发函数）。只关心未来到目标的希望。
A*	f(n) = g(n) + h(n)	同时考虑历史成本（g(n)）和未来希望（h(n)）。

这个代价函数的差异，导致了它们完全不同的行为。

1. Dijkstra 算法：严谨的实干家

• 策略：f(n) = g(n)
  • 它像一个不知疲倦、严谨的实干家。它只相信已经走过的路，总是优先扩展从起点过来总实际代价最小的节点。
• 优点：保证找到最短路径。
• 缺点：没有方向性。它会以起点为中心，向所有方向“均匀”地探索，直到最终碰到目标为止。这个过程可能会很慢，因为它探索了很多不相关的区域。

搜索过程图示：像一个以起点为圆心的圆形不断向外扩散。

2. GBFS 算法：贪婪的冒险家

• 策略：f(n) = h(n)
  • 它像一个被目标吸引的贪婪冒险家。它不关心已经走了多远（g(n)），只关心“目标离我还有多远？”。它总是优先扩展离终点估计代价最近的节点。
• 优点：通常非常快。它非常有方向性地直奔目标而去，不会在无关区域浪费时间。
• 缺点：不保证找到最短路径。因为它忽略了已经走过的路径成本，可能会被误导进一条看似离目标很近、但实际上非常绕远的路径。

搜索过程图示：像一个被磁铁吸引的箭头，直奔目标，但可能会撞墙和绕路。

直观比喻

假设你要从北京开车去上海，寻找最短时间的路径。

• Dijkstra：它会仔细计算从北京出发，到每一个路口、每一个城市的总耗时。它不关心这个城市是不是在去上海的方向上，它只关心“从北京到这里我花了多少时间”。它会先探索所有耗时短的可能路径，最终确保找到全局最快的那条。可靠，但可能研究了去石家庄、郑州等所有方向的路。
• GBFS：它只盯着地图看“哪个城市离上海直线距离最近？”。它看到天津离上海好像近一点，就先去天津；然后从天津看，济南好像更近，就去济南……它永远选择“看起来”离目标最近的下一个点。很快，但可能不小心被引上了一条山路或者拥堵的小路，最终总时间并不是最短的。
• A*：它既会考虑“从北京开到这里已经花了多少时间”（g(n)），也会考虑“从这里到上海估计还要花多少时间”（h(n)）。它平衡了历史和未来，既高效又可靠。

总结与关系

特性	Dijkstra	GBFS	A* (作为对比)
代价函数	f(n) = g(n)	f(n) = h(n)	f(n) = g(n) + h(n)
保证最短路径?	是	否	是 (如果启发函数满足条件)
速度	慢	非常快	快 (在Dijkstra和GBFS之间)
行为	向四周均匀扩展，无方向性	贪婪地直奔目标，方向性极强	有方向性地向目标搜索

关系结论：

GBFS 和 Dijkstra 是A*算法的两个极端特例：

• 当 A* 的启发函数 h(n) = 0 时，A* 就退化成了 Dijkstra。
• 当 A* 的实际代价函数 g(n) = 0 时，A* 就退化成了 GBFS。

因此，它们不是直接的改进关系，而是设计哲学上的取舍：

• Dijkstra 用速度换取了最优性的保证。
• GBFS 用最优性的保证换取了速度。

在实际应用中，A* 因其在速度和最优性之间的平衡而成为最常用的寻路算法。而当你需要极速找到一个“足够好”的路径，而非“最佳”路径时，GBFS 会是一个不错的选择。

寻路算法核心特性对比总表

算法	代价函数 f(n)	数据结构	是否保证最短路径？	优点	缺点	搜索行为比喻
BFS	(隐含 f(n) = g(n), 且权值=1)	队列	是 (等权图)	简单，保证最短路径（步数最少）	效率低，无方向性，内存消耗大	圆形涟漪：均匀地向所有方向扩散
DFS	无（按深度优先）	栈	否	内存消耗相对少（仅存储一条路径）	极易找到非常绕的路径，可能陷入死循环	钻探者：一条路走到黑，碰壁再回头
Dijkstra	f(n) = g(n)	优先队列	是 (带权图)	能处理不同权重，保证最短路径（代价最小）	比BFS/DFS慢，无方向性，探索区域大	严谨的实干家：不计方向，只扩展已花费代价最小的点
GBFS	f(n) = h(n)	优先队列	否	通常非常快，方向性极强	贪心，易被误导，结果可能非最优	贪婪的冒险家：只看终点方向，直奔而去
A*	f(n) = g(n) + h(n)	优先队列	是 (启发函数可采纳时)	效率与最优性的完美平衡，方向性好	启发函数设计影响性能	聪明的规划师：平衡已花费代价和未来预期

---

详细分解

1. 广度优先搜索（BFS）

• 核心思想：系统性地、逐层地探索所有可能的路径。
• 数据结构：队列（FIFO）。先进先出的规则保证了先被访问的节点（即离起点更近的节点）会先被扩展。
• 与Dijkstra的关系：在所有边权值都为1的图中，BFS就是Dijkstra算法。因为此时“步数最少”就等于“代价最小”。BFS是Dijkstra在等权图下的一个高效特例实现。
• 适用场景：查找社交网络中的最短关系链、解决迷宫问题（保证最短步数）、网络爬虫等。

2. 深度优先搜索（DFS）

• 核心思想：尽可能深地探索一条路径，直到无法继续再回溯。
• 数据结构：栈（LIFO）。后进先出的规则保证了总是扩展最新发现的节点。
• 与其他算法的关系：DFS与上述寻路算法哲学完全不同。它不追求最优，而是一种暴力穷举策略。在寻路中表现很差，但适用于许多其他问题（如拓扑排序、检测环路、求解数独等）。
• 适用场景：不适合用于典型的最短路径寻路。适用于需要遍历所有可能性的场景，如排列组合、图的连通性检测。

3. Dijkstra 算法

• 核心思想：追求全局最优。它总是确信地选择当前已知的、从起点出发总实际代价最小的节点进行扩展，直到到达终点。
• 代价函数：f(n) = g(n)。g(n)是确切的、累积的历史成本。它完全忽略目标点的位置信息。
• 适用场景：网络路由协议（如OSPF）、地图导航（当不考虑启发式信息时）、任何需要在带权图中找单源最短路径的场景。

4. 贪心最佳优先搜索（GBFS）

• 核心思想：追求局部最优（贪婪）。它总是选择“看起来”离目标最近的点，希望这样能最快到达终点。
• 代价函数：f(n) = h(n)。h(n)是一个启发式函数，是对未来成本的估计（如直线距离）。它完全忽略已经走了多远。
• 适用场景：对路径质量要求不高、但对速度要求极高的场景，或者在大规模地图中快速找到一个“还不错”的初始解。

5. A*（A-Star）算法

• 核心思想：平衡历史成本与未来估计。它不像Dijkstra那样盲目，也不像GBFS那样冲动。它的代价函数是两部分之和。
• 代价函数：f(n) = g(n) + h(n)。
  • g(n)：确保路径的正确性（朝着最短路径的方向努力）。
  • h(n)：引导搜索的方向性（朝着目标点的方向努力）。
• 关键：如果启发函数 h(n) 是可采纳的（即永远不会高估到达目标的实际代价），则A*保证能找到最短路径。常见的h(n)有曼哈顿距离、对角线距离、欧几里得距离。
• 适用场景：绝大多数游戏AI的寻路、机器人路径规划。它是实践中最常用、最有效的寻路算法。

直观图示与总结

想象一下在迷宫中寻找出口：

• BFS：你会派出一大群人，手拉手并排向前走，确保不漏掉任何一条近路。稳妥但人力消耗大。
• DFS：你会随机选一条路一直走，走到死胡同就原路返回，再试下一个岔路口。运气好很快，运气差极慢。
• Dijkstra：你有一个精密的计步器。你每到一个路口，就计算从起点到这里的确切步数，然后总是从步数最少的路口继续探索。绝对能找到最短路径，但可能探索了太多死胡同。
• GBFS：你有一个指向终点的指南针。你永远选择指南针指向最准的方向前进。很快就能找到路，但找到的路可能不是最短的，因为你可能被一堵墙挡住，要绕很远。
• A：你既有一个计步器，又有一个指南针。你选择的标准是 “已走步数 + 指南针预估的剩余步数”最小的方向。既能高效地朝向目标，又不会偏离最短路径太远*。

最终建议：在需要寻找最短路径的场合，A* 算法通常是默认的最佳选择。理解其他算法有助于你更深刻地理解A的原理，并在特定约束下（如内存极度受限时考虑IDA，或网格地图中考虑JPS）做出更优的选择。

简单画图示意

只能上下左右走，不能斜着走。

BFS

隐含 f(n) = g(n), 且权值=1，从起点到当前节点 n 的实际代价都是1，所以只有到遍历到终点才知道路径（步数最少）。

图中画的都是最少步数，其实权值都是1。

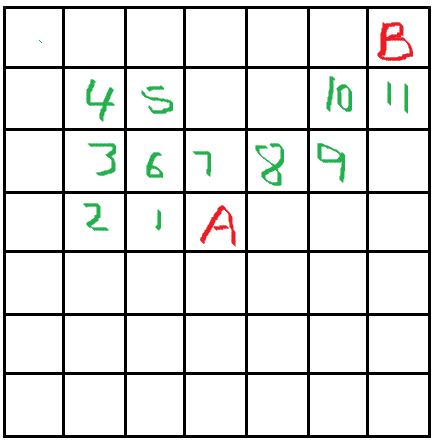
DFS

一条路走到黑，碰壁再回头。运气好直接找到一条通往终点的路径，运气不好最后一条才找到，而且路径长度不一定，可能很绕。

图中画的都是最少步数，其实权值都是1。

Dijkstra

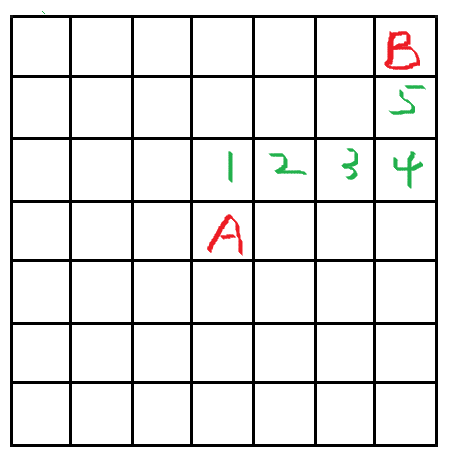
f(n) = g(n)，从起点到当前节点 n 的实际代价。用什么函数计算 g(n)，完全取决于你的具体应用场景和想要优化的目标。可以是步数、距离、时间、能量、综合成本等等...

这里用步数计算。

GBFS

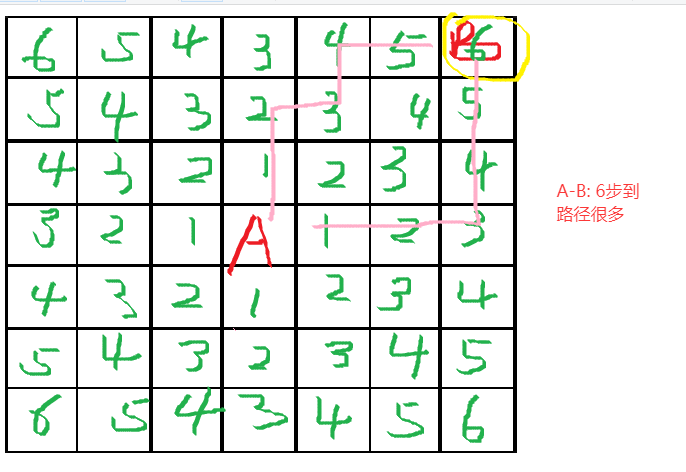
f(n) = h(n)。h(n)是一个启发式函数，是对未来成本的估计（如直线距离）。它完全忽略已经走了多远。常见的h(n)有曼哈顿距离、对角线距离、欧几里得距离。

这里用曼哈顿距离：d(P1,P2)=∣x1−x2∣+∣y1−y2∣，例如点 A(1,2)和 B(4,6) 的距离为 ∣1−4∣+∣2−6∣=7。

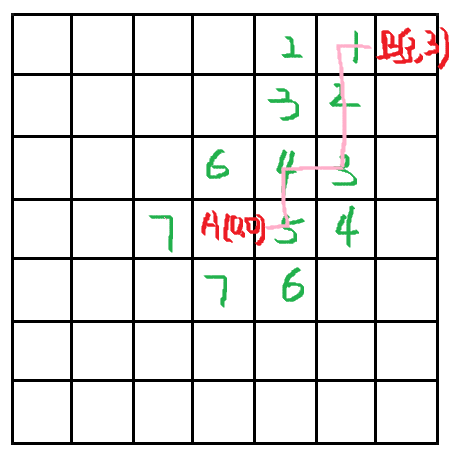
A*

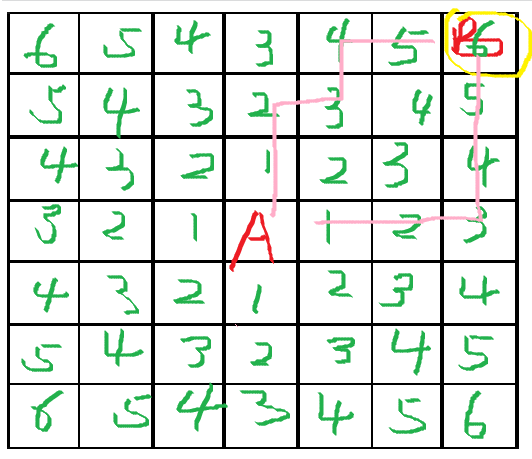
f(n) = g(n) + h(n)，同时考虑历史成本（g(n)）和未来希望（h(n)）。

h(n)是一个启发式函数，这里用曼哈顿距离：d(P1,P2)=∣x1−x2∣+∣y1−y2∣，例如点 A(1,2)和 B(4,6) 的距离为 ∣1−4∣+∣2−6∣=7。

可参考：

Introduction to the A* Algorithm