算法一：线性回归

模型推导：

示例：已知年龄x1和工资x2，向银行贷款，贷款额度y

假设年龄x1的参数是w1，工资x2的参数是w2；w0为偏置项

拟合的平面：h(x) = w0 + w1x1 + w2x2

假设w0也乘一个x0，x0=1，则不影响计算结果，因此整合以上公式：

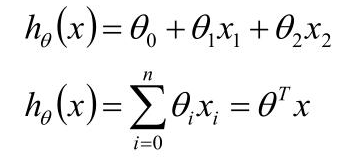
 对于每一个样本，如图所示，红色的点为真实值，真实值与拟合平面存在差值，这是不可避免的，这个差值，称为误差。

 对以上公式，加入误差，进一步优化为以下公式

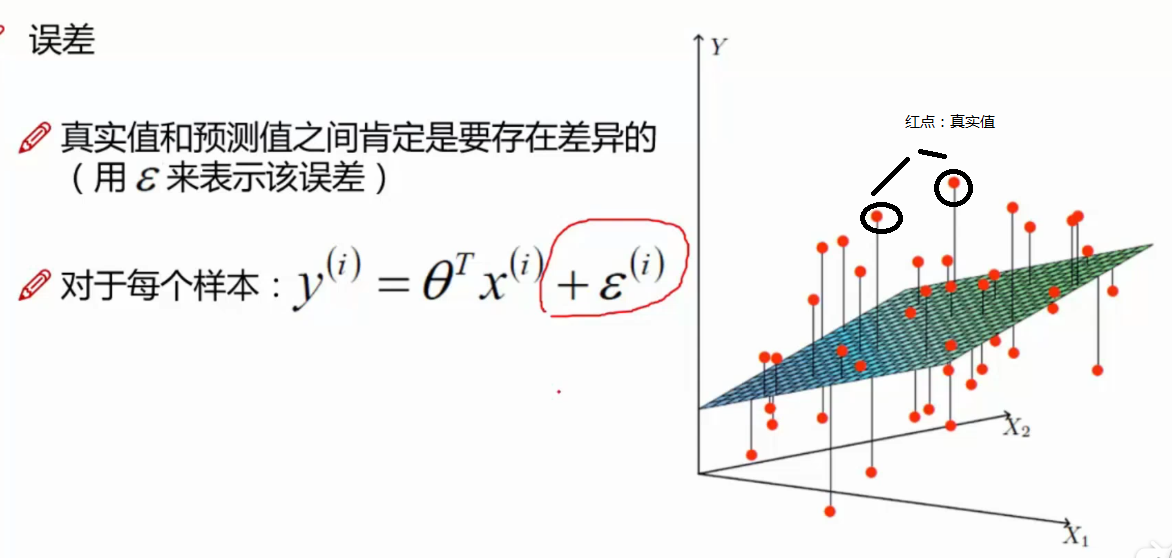
模型假定好后，我们把训练数据代入上面的设定模型中，可以通过模型预测一个样本最终值；

 

独立：张三和李四一起来贷款，他俩没关系

同分布：他俩都来得是我们假定的这家银行

机器学习，建立在独立同分布的基础之上。

高斯分布图：大部分取值在-1和1之间，越接近-4和4两端的分布越少

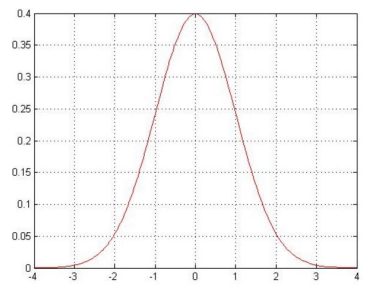
由于误差服务从高斯分布，求出误差的表达式：

 

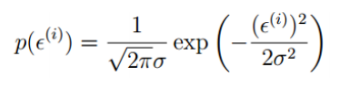
将误差的表达式，代入上面的样本模型表达式，推导结果为：

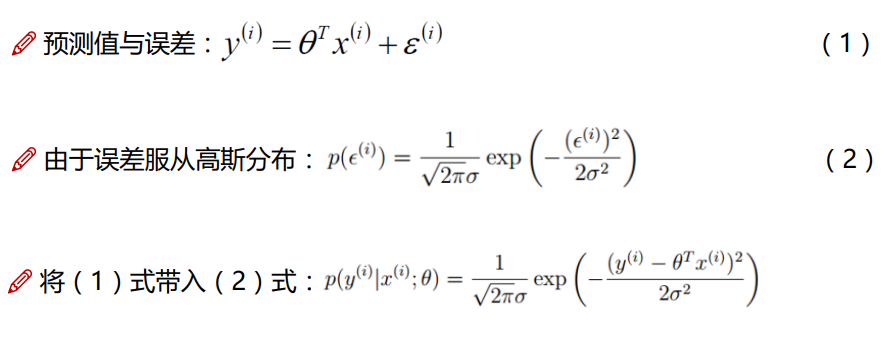
如上面可知，对于每一个样本 x ,代入到 p (y |x ;θ) 都会得到一个y 的概率；又因为设定样本是独立同分布的；对其求最大似然函数：

以上过程，由数据推导参数：得到什么样的参数跟我们的数据组合后恰好是真实值，即由数据得到什么样的参数是最好的。

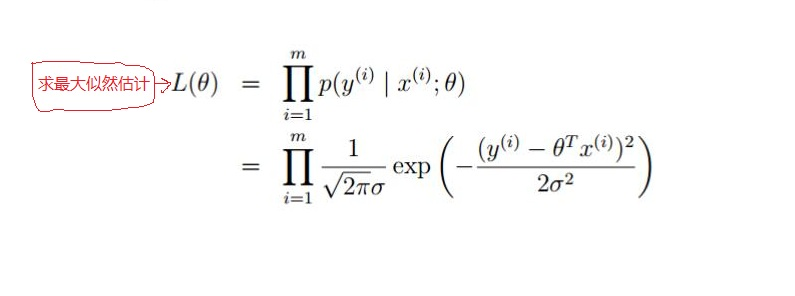
以上公式，使用的乘法，难解，加法容易；使用对数似然函数，将乘法转换成加法

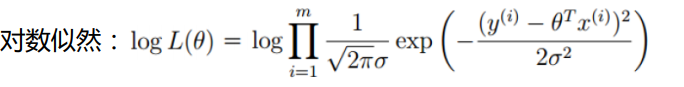
使用对数似然，进行化简：

似然函数越大越好：

以上就得到了回归的损失函数最小二乘法的公式，对于好多介绍一般对线性回归的线性损失函数就直接给出了上面的公式二乘法。下面我们就对上面做了阶段性的总结：线性回归，根据大数定律和中心极限定律假定样本无穷大的时候，其真实值和预测值的误差ε 的加和服从u=0,方差=δ²的高斯分布且独立同分布，然后把ε =y-Øx 代入公式，就可以化简得到线性回归的损失函数；

    第二步：对损失函数进行优化也就是求出w,b，使的损失函数最小化；

第一种方法使用矩阵（需要满足可逆条件）

x为特征项，y为贷款额度，在多数情况下，都可以求出 θ

 

 以上就是按矩阵方法优化损失函数，但上面方法有一定的局限性，就是要可逆；下面我们来说一说另外一个优化方法 梯度下降法；对于梯度下降法的说明和讲解资料很多，深入的讲解这里不进行，可以参考：http://www.cnblogs.com/ooon/p/4947688.html这篇博客，博主对梯度下降方法进行了讲解

 梯度下降：梯度，即前面求的偏导；下降，求的是偏导下降

引入：当我们得到了一个目标函数后，如何进行求解？ 直接求解？（并不一定可解，线性回归可以当做是一个特例）

常规套路：机器学习的套路就是我交给机器一堆数据，然后告诉它 什么样的学习方式是对的（目标函数），然后让它朝着这个方向去做

如何优化：一口吃不成个胖子，我们要静悄悄的一步步的完成迭代 （每次优化一点点，累积起来就是个大成绩了）

 

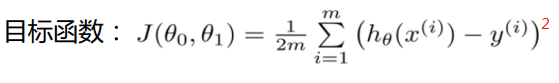
梯度下降，就是寻找上图中山谷的最低点，也就是目标函数的终点。(就是寻找什么样的参数能够使得目标函数达到极值点)

下山分几步走呢？（更新参数）

（1）：找到当前最合适的方向

（2）：走那么一小步，走快了该”跌倒 ”了

（3）：按照方向与步伐去更新我们的参数

总体流程就如上所示，就是求出每个变量的梯度；然后顺着梯度方向按一定的步长a,进行变量更新；下面我们就要求出每个变量的梯度，下面对每个θ进行梯度求解公式如下：

 

 如上我们求出变量的梯度；然后迭代代入下面公式迭代计算就可以了：

 

 

 上面每次更新变量，都要把所有的样本的加起来，数据量大的时候效率不高，下面还有一种就是按单个样本进行优化，就是随机梯度下降：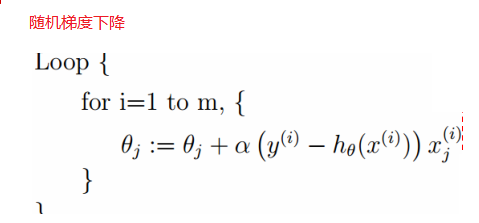

 

 

 

按上面优化步骤就可以求出w,b,就可以获得优化的特征方程：

#!/usr/bin/python
# -*- coding:utf-8 -*-
 
import numpy as np
import warnings
from sklearn.exceptions import  ConvergenceWarning
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression,RidgeCV,LassoCV,ElasticNetCV
import matplotlib as mpl
import matplotlib.pyplot as plt
 
if __name__ == "__main__":
 
    warnings.filterwarnings(action='ignore', category=ConvergenceWarning)
    np.random.seed(0)
    np.set_printoptions(linewidth=1000)
    N = 9
    x = np.linspace(0, 6, N) + np.random.randn(N)
    x = np.sort(x)
    y = x**2 - 4*x - 3 + np.random.randn(N)
    x.shape = -1, 1
    y.shape = -1, 1
    p =Pipeline([
        ('poly', PolynomialFeatures()),
        ('linear', LinearRegression(fit_intercept=False))])
    mpl.rcParams['font.sans-serif'] = [u'simHei']
    mpl.rcParams['axes.unicode_minus'] = False
    np.set_printoptions(suppress=True)
    plt.figure(figsize=(8, 6), facecolor='w')
    d_pool = np.arange(1, N, 1)  # 阶
    m = d_pool.size
    clrs = []  # 颜色
    for c in np.linspace(16711680, 255, m):
        clrs.append('#%06x' % c)
    line_width = np.linspace(5, 2, m)
    plt.plot(x, y, 'ro', ms=10, zorder=N)
    for i, d in enumerate(d_pool):
        p.set_params(poly__degree=d)
        p.fit(x, y.ravel())
        lin = p.get_params('linear')['linear']
        output = u'%s：%d阶，系数为：' % (u'线性回归', d)
        print output, lin.coef_.ravel()
        x_hat = np.linspace(x.min(), x.max(), num=100)
        x_hat.shape = -1, 1
        y_hat = p.predict(x_hat)
        s = p.score(x, y)
        z = N - 1 if (d == 2) else 0
        label = u'%d阶，$R^2$=%.3f' % (d, s)
        plt.plot(x_hat, y_hat, color=clrs[i], lw=line_width[i], alpha=0.75,label=label, zorder=z)
        plt.legend(loc='upper left')
        plt.grid(True)
       # plt.title('线性回归', fontsize=18)
        plt.xlabel('X', fontsize=16)
        plt.ylabel('Y', fontsize=16)
    plt.show()

 

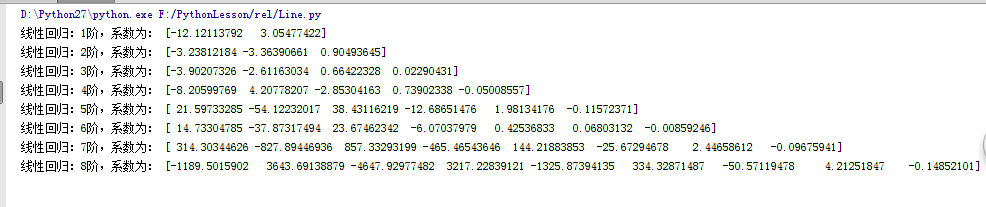
 图像显示如下：

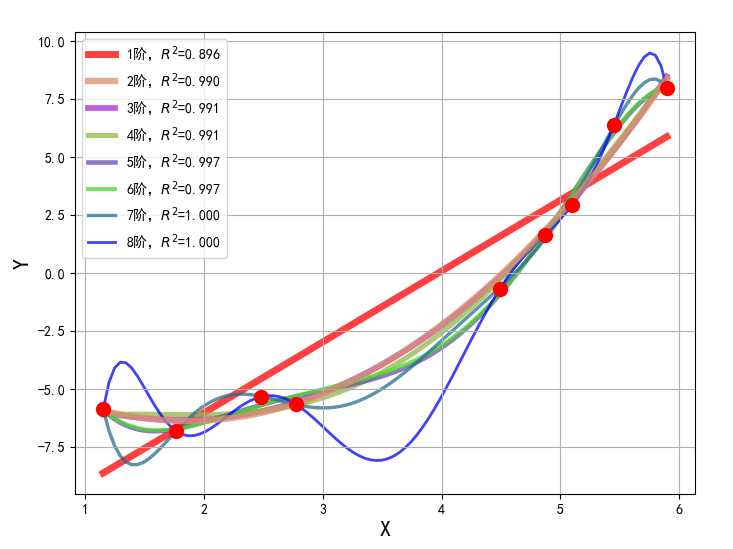
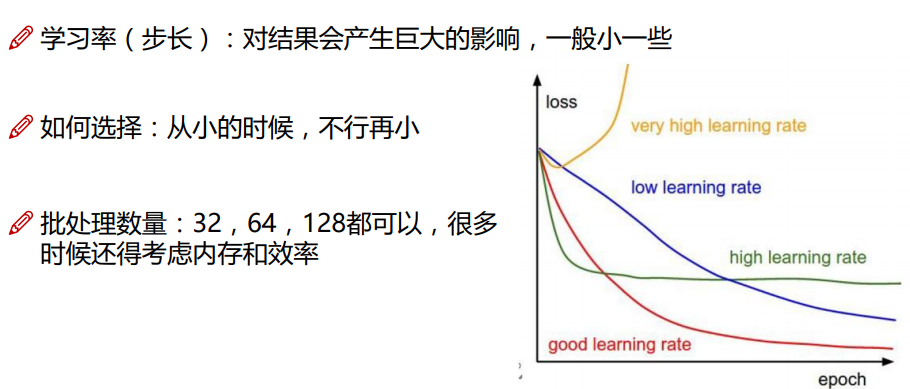
从上面图像可以看出，当模型复杂度提高的时候，对训练集的数据拟合很好，但会出现过度拟合现象，为了防止这种过拟合现象的出现，我们在损失函数中加入了惩罚项，根据惩罚项不同分为以下：

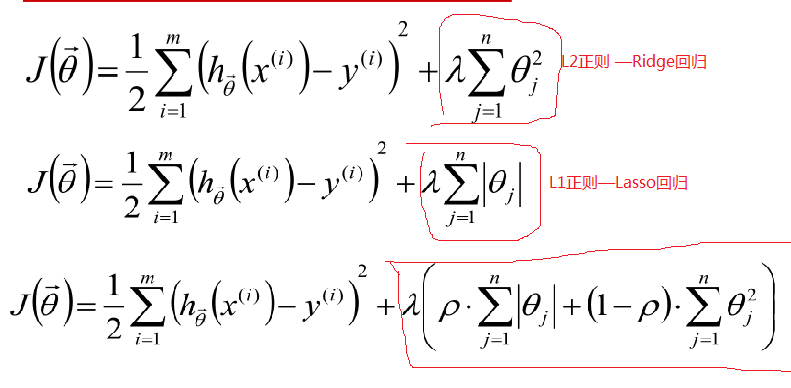
最后一个为Elastic Net 回归，把 L1 正则和 L2 正则按一定的比例结合起来：

L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。Lasso在特征选择时候非常有用，而Ridge就只是一种规则化而已。在所有特征中只有少数特征起重要作用的情况下，选择Lasso比较合适，因为它能自动选择特征。而如果所有特征中，大部分特征都能起作用，而且起的作用很平均，那么使用Ridge也许更合适。对于各种回归的比较可以看下图：

 

参考：https://blog.csdn.net/lisi1129/article/details/68925799?utm_source=copy 

参考：https://blog.csdn.net/lc013/article/details/55002463