线性代数六:矩阵的进一步运算示例
一、矩阵的基本运算
题一:
两个矩阵相乘,不能得出如下结论:

两个矩阵相乘等于0,也不能推出任何一个矩阵等于0。但是可以推出两个结论:
方程组AX=0的解,和两个矩阵的秩之和小于n
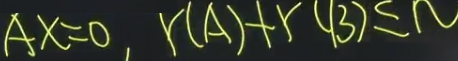

题二:

结论:AB=A-B或AB=A+B,且A,B都是n阶矩阵,可以得出AB互为逆矩阵 。也可称为,A,B可交换。
总结,两个矩阵可交换的四种情况:
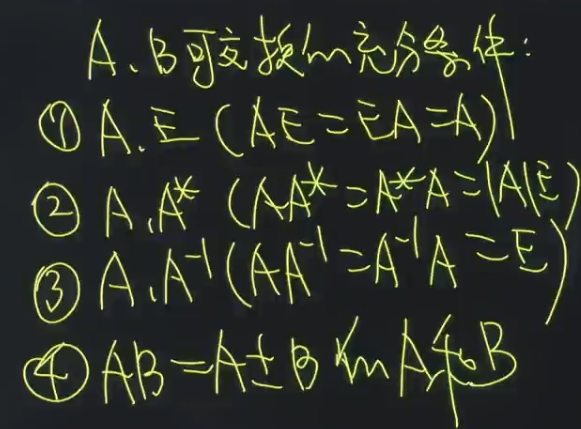
二、特殊方阵的幂:
题 一:
行向量与列向量,相乘的结论:列向量 * 行向量,得到的 n阶方阵;行向量 * 列向量,得到的是一个数。
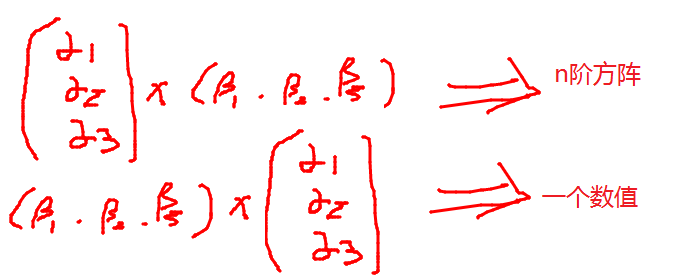

题 二:
直接利用以上的结论:任意两行两列均成比例型,即秩为1型,可得

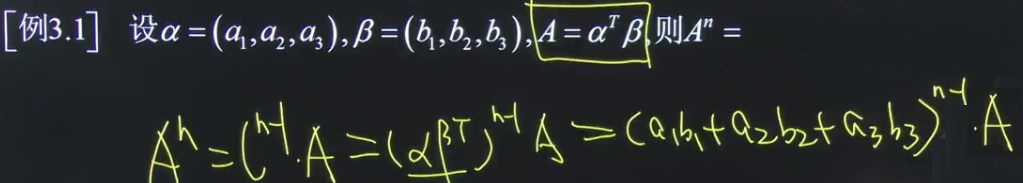
题三:
同样,分析可知,矩阵A任意两行成比例,任意两列成比例,可以直接使用上面的公式
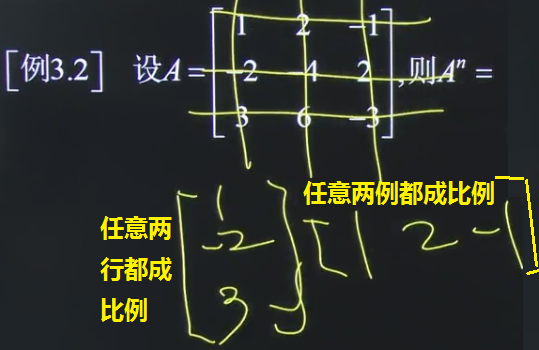
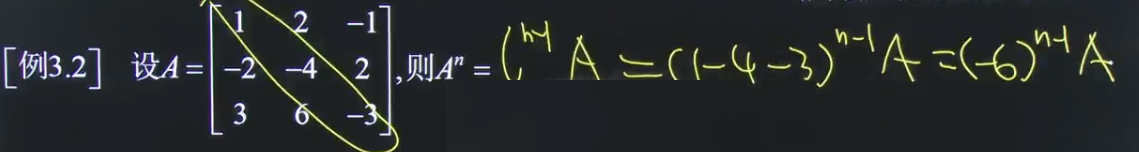
题二和题三的两种形式成比例,可以相互转化:
题三的矩阵A任意两行,任意两列成例,可以转化成A=abT形式:
其中,列向量a * 行向量bT,列向量a为各行的最简比,行向量bT为各列的最简比。

题四:

题五:
不是任意两行两行成比例的情况,拆分矩阵,然后利用第四题的结论:

相似和归纳法:

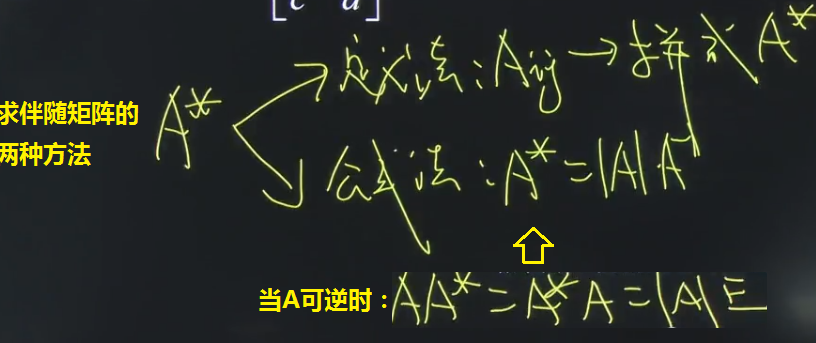
三、求伴随矩阵 ![]()
题一:

如果已知伴随矩阵,求它的逆矩阵呢?
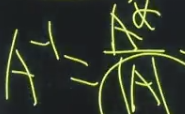
题 二:
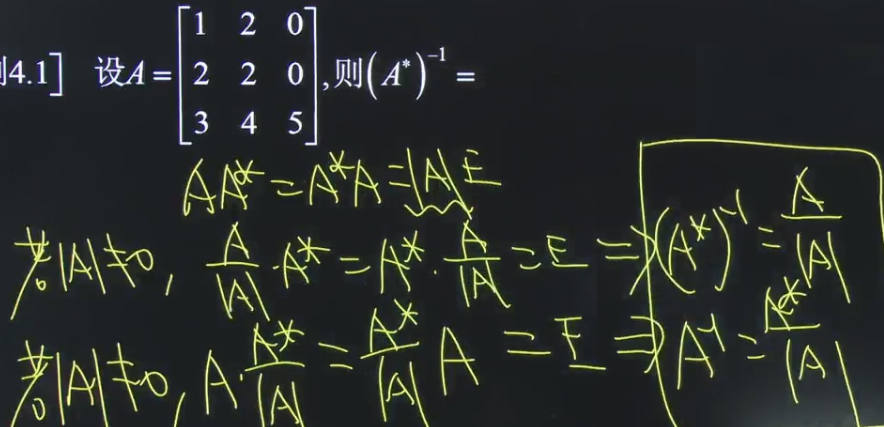
题三:
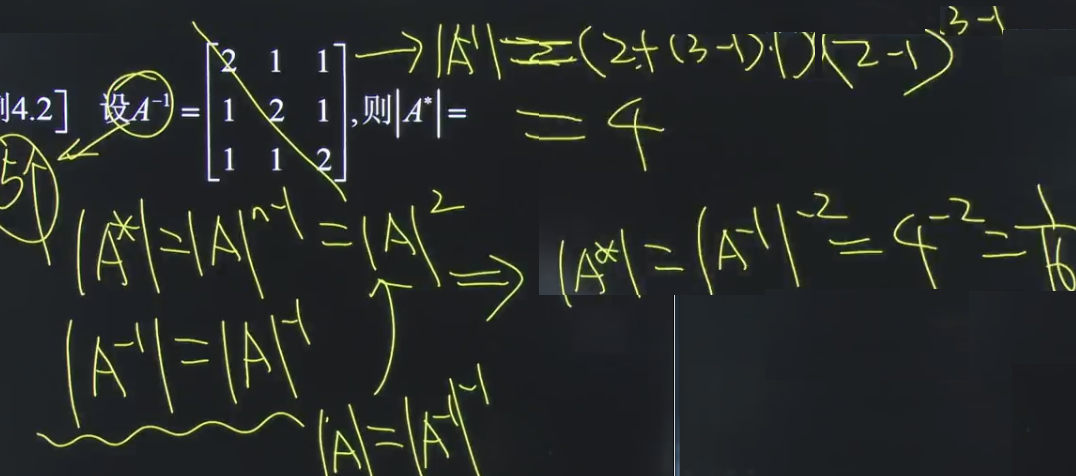
四、可逆矩阵
阶数不高的数值型矩阵,求逆矩阵,一般用矩阵初等行变换,略。
矩阵阶降:使用分块矩阵。
题一:
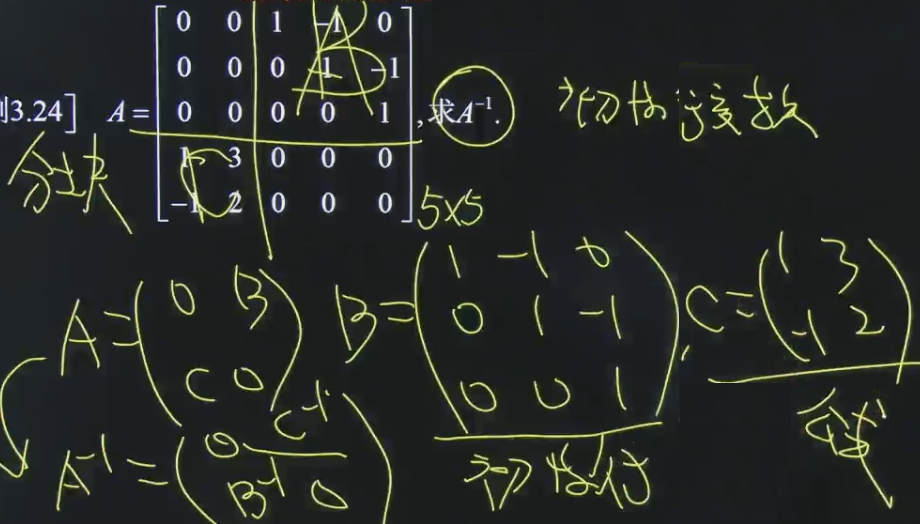
题二:

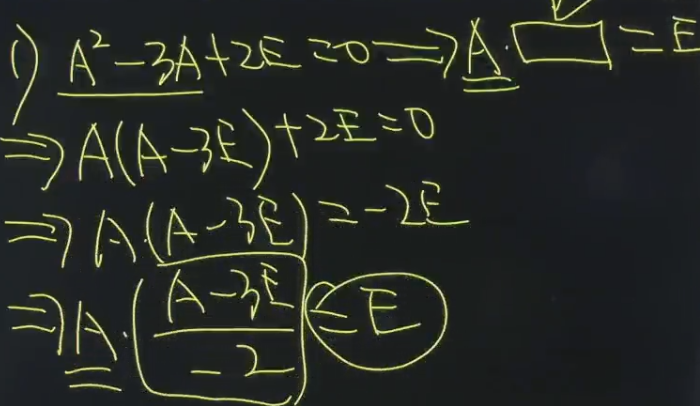
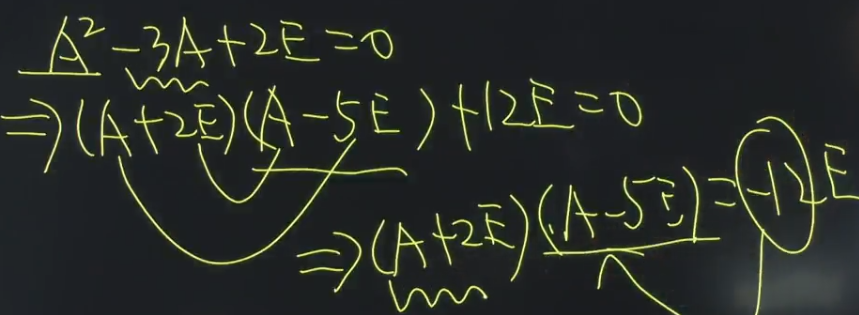

题三:

题四:

题五、六:
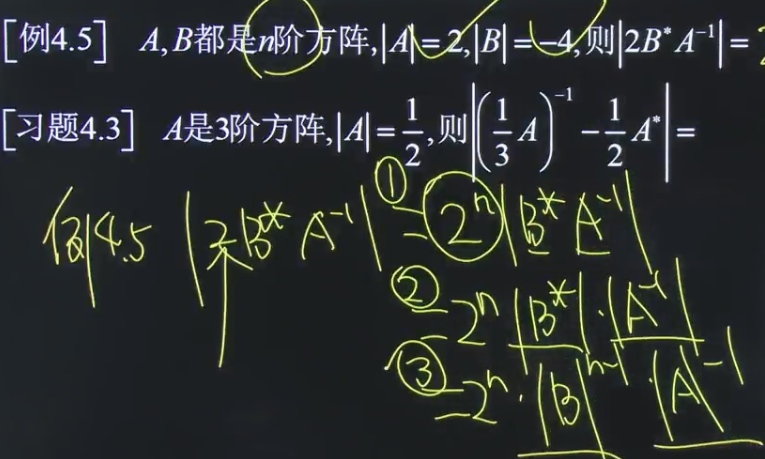


题七:
这个题两个矩阵A,B没有关联,只能使用矩阵的初等变形。
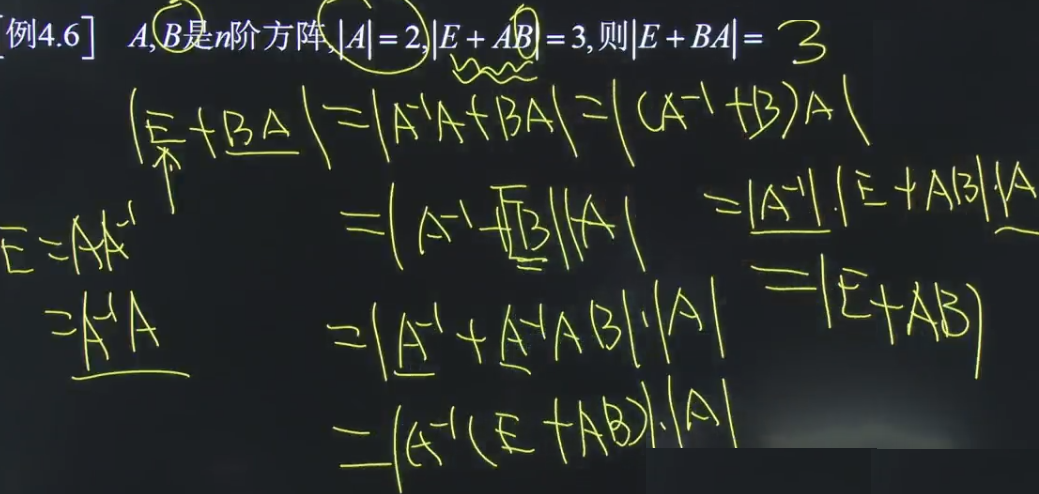
posted on 2019-02-03 08:24 myworldworld 阅读(1247) 评论(0) 收藏 举报



 浙公网安备 33010602011771号
浙公网安备 33010602011771号