线性代数三：行列式的计算二

 四、余子式、代数余子式求和

题 一：

利用行列式的性质，可知：

如果将(1)看作第4行与它的代数余子式这和，那么它等于行列式的值。而行列式的行(列)成比例，则行列式的值为0

如果将(1)看作对第3行的，行列式的串行展开，那么它等于0 

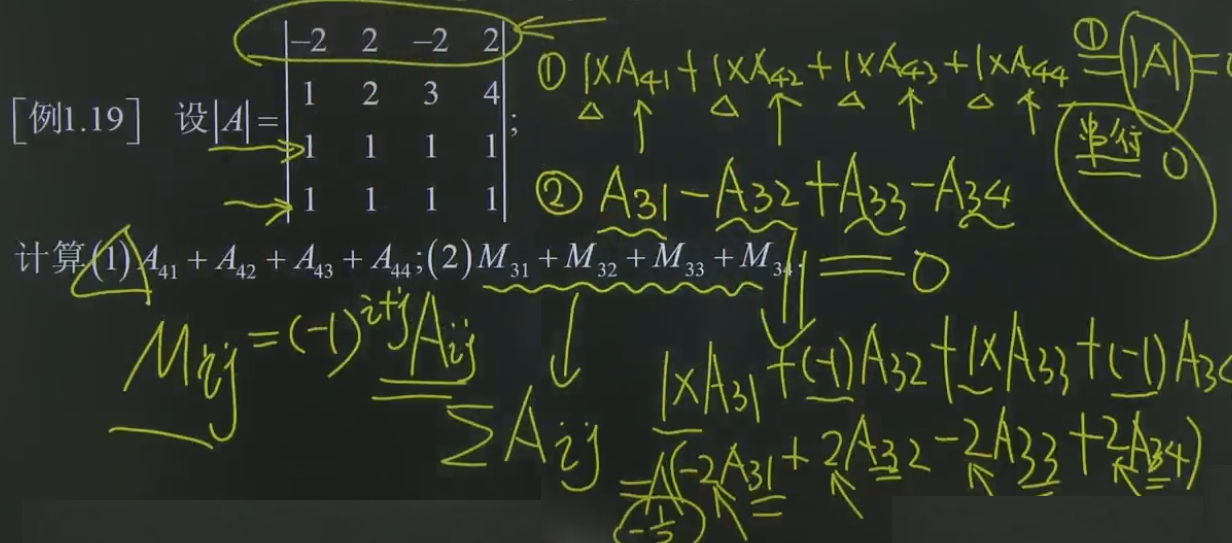
题二：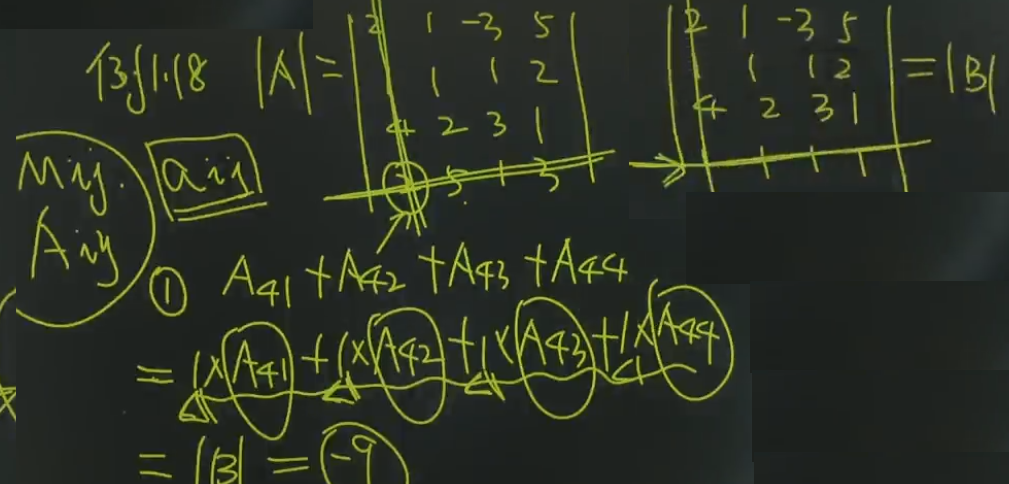

二、行列式的值是否为0

题 一：

题 二：

方法一：反证法

在代数中，只要看到行列式AB=0，就可以得出以下两个结论：

 

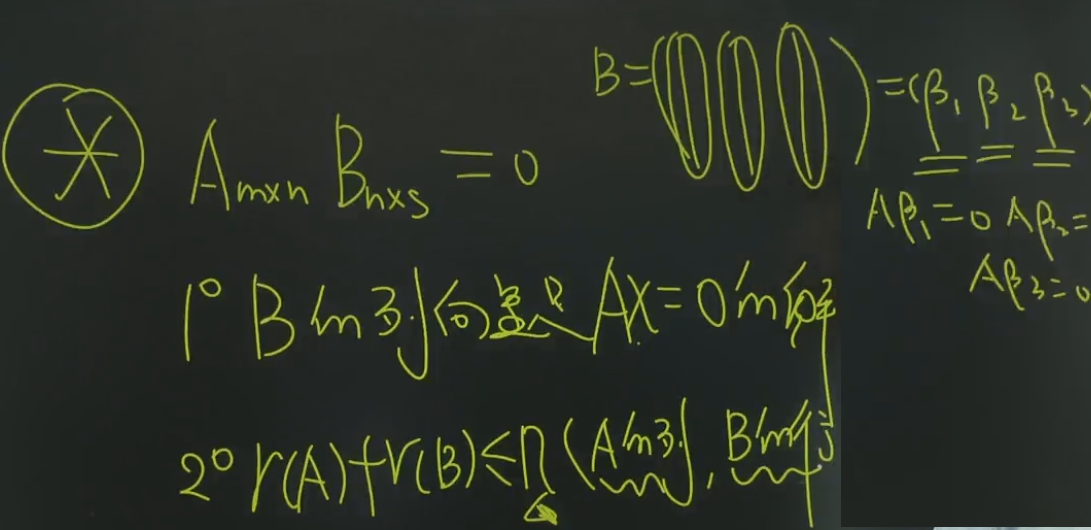
方法二：齐次方程组的思想

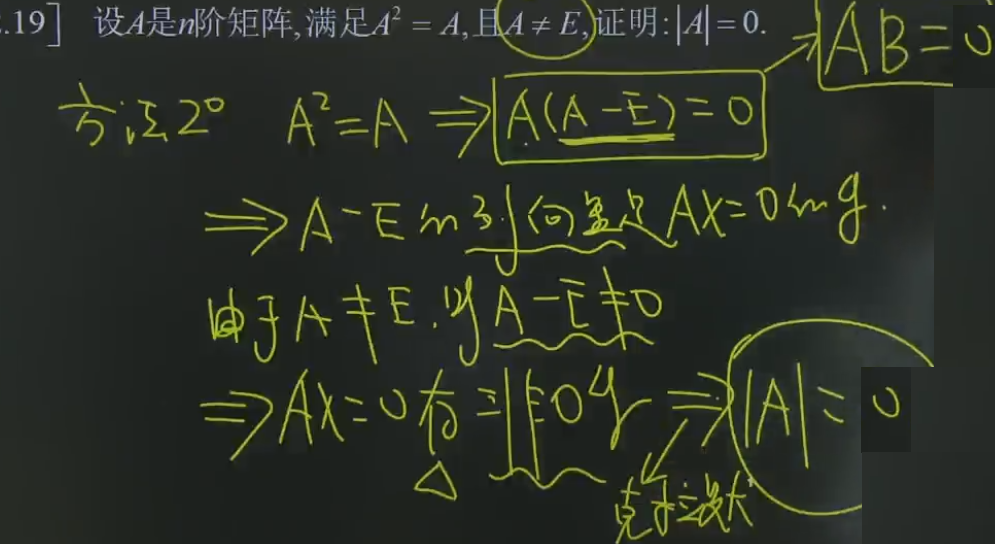
方法三：秩

 

 

克拉默法则：

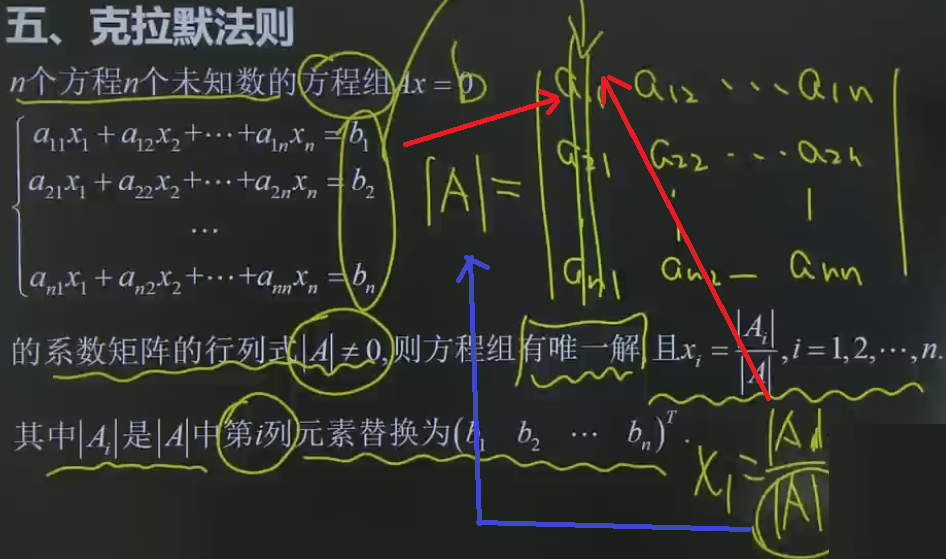
A1行列式，就是用(b1 b2... bn)代替A的第1列形成的新的行列式。

Ai的行列式，就是用(b1 b2... bn)代替A的第i列形成的新的行列式。

用克拉默法则解方程，需要解n+1个行列式，因此它不是用来解方程的。而是用来判断方程是否有解。 

由克拉默法则推出：  

 

题 三：

此题 必须由克拉默法则解方程组。

系数矩阵A：

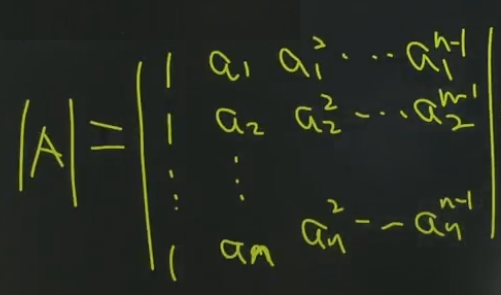
A的转置矩阵：

利用行列式的几个重要公式中的范德蒙法则，可知，它不等于0

然后根据克拉默法则，可求得，x1=1,

x2,..xn=0

题三：

 

 题四：

将某行(列)转化为两个0，然后用行列式的展开。