算法五:排序、搜索(算法部分)
一、排序
排序算法:能将一串数据按照某特定顺序进行排列的一种算法。
常用排序:
|
名称 |
复杂度 |
说明 |
备注 |
|
冒泡排序 |
O(N*N) |
将待排序的元素看作是竖着排列的“气泡”,较小的元素比较轻,从而要往上浮 |
|
|
插入排序 Insertion sort |
O(N*N) |
逐一取出元素,在已经排序的元素序列中从后向前扫描,放到适当的位置 |
起初,已经排序的元素序列为空 |
|
选择排序 |
O(N*N) |
首先在未排序序列中找到最小元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小元素,然后放到排序序列末尾。以此递归。 |
|
|
快速排序 Quick Sort |
O(n *log2(n)) |
先选择中间值,然后把比它小的放在左边,大的放在右边(具体的实现是从两边找,找到一对后交换)。然后对两边分别使用这个过程(递归)。 |
|
|
堆排序HeapSort |
O(n *log2(n)) |
利用堆(heaps)这种数据结构来构造的一种排序算法。堆是一个近似完全二叉树结构,并同时满足堆属性:即子节点的键值或索引总是小于(或者大于)它的父节点。 |
近似完全二叉树 |
|
希尔排序 SHELL |
O(n1+£) 0<£<1 |
选择一个步长(Step) ,然后按间隔为步长的单元进行排序.递归,步长逐渐变小,直至为1. |
|
|
箱排序 |
O(n) |
设置若干个箱子,把关键字等于 k 的记录全都装入到第k 个箱子里 ( 分配 ) ,然后按序号依次将各非空的箱子首尾连接起来 ( 收集 ) 。 |
分配排序的一种:通过" 分配 " 和 " 收集 " 过程来实现排序。 |

在实际场景中,快排用得比较多,因为它的平均效率为O(n*log2n),且很少出现O(n*n)的情况,且不像归并排序需要占用更多的空间。
1.冒泡排序(Bubble Sort):一种比较简单的算法
时间复杂度:稳定,平均O(n*n),最优O(n),最坏O(n*n)
辅助空间:O(1)
冒泡排序:它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。
走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端,故名。
data_set = [9, 1, 22, 31, 45, 3, 6, 2, 11] loop_count = 0 for j in range(len(data_set)): # 循环n次 # (循环n-已循环次数) + ... + (循环n-已循环次数)= (n-1) + (n-2)+.....+(n-(n-1)) for k in range(len(data_set) - (j+1)): if data_set[k] > data_set[k + 1]: tmp = data_set[k] data_set[k] = data_set[k + 1] data_set[k + 1] = tmp loop_count += 1 print("loop times>>>>>>", loop_count) # 36 print("data_set>>>>>>", data_set)
2.选择排序O(N*N):
时间复杂度:不稳定,平均O(n*n),最优O(n*n),最坏O(n*n)
辅助空间:O(1)
首先在未排序序列中找到最小元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小元素,然后放到排序序列末尾。以此递归。
示例一:
data_set = [9, 1, 22, 31, 45, 3, 6, 2, 11] smallest_num_index = 0 # 初始列表最小值,默认为第一个 loop_count = 0 for j in range(len(data_set)): # 循环n次 for k in range(j, len( data_set)): # (循环n-已循环次数) + ... + (循环n-已循环次数)= (n-1) + (n-2)+.....+(n-(n-1)) if data_set[k] < data_set[smallest_num_index]: # 当前值 比之前选出来的最小值 还要小,那就把它换成最小值 smallest_num_index = k loop_count += 1 print("smallest num is ", data_set[smallest_num_index]) tmp = data_set[smallest_num_index] data_set[smallest_num_index] = data_set[j] data_set[j] = tmp print("loop times>>>>>>", loop_count) # 45 print("data_set>>>>>", data_set)
示例二:
j = 0 # 第1个元素0~倒数第2个元素n-2
# i:第2个元素1~最后一个元素n-1
# 1.用第一个元素32同剩余元素比较,得到最小元素1的索引min为3
min = 3
# 将找到的最小值1依次放在左边:即,将第0个元素和第3个元素交换
alist[0], alist[3] = alist[0], alist[0]
alist = [1, 20, 8, 32, 99, 98, 200, 299]
j = 0 # 第2个元素1~倒数第2个元素n-2
# i: 第3个元素2~最后一个元素n-1
# 2.用第二个元素20同剩余元素比较,得到最小元素8的索引min为2
min = 2
# 2.将找到的最小值1依次放在左边:即,将第1个元素和第2个元素交换
alist[1], alist[2] = alist[2], alist[1]
alist = [1, 3, 20,32, 99, 98, 200, 299]
以此类推到最后一个元素,这是选择排序,始终从右边的剩余的列表中选出最小值,放在左边
alist = [32, 20, 8, 1, 99, 98, 200, 299] # 用代码表示: def select_sort(alist): n = len(alist) for j in range(n-1): # j: 0~n-2,时间复杂度:O(n-1) min_index = j for i in range(j+1, n): # i: 1~n-1,时间复杂度比O(n-1)小,近似为n if alist[min_index] > alist[i]: min_index = i # 时间复杂度:O(n-2) + O(n-3) + ...1等于O((n-2+1)*(n-2)/2) alist[j], alist[min_index] = alist[min_index], alist[j] print("result>>>>>", alist) select_sort(alist) # 总的时间复杂度: # 1: O((n-1)*(n-2)/2)=O((n-2)*(1+(n-2)/2),约等于O(n*n) # 2: 内层比n-2小,近似看作n,等于O(n)*O(n)
3.插入排序:
时间复杂度:稳定,平均O(n*n),最优O(n),最坏O(n*n)
辅助空间:O(1)
将列表分为2部分,左边为排序好的部分,右边为未排序的部分,
循环整个列表,每次将一个待排序的记录,按其关键字大小插入到前面已经排好序的子序列中的适当位置,直到全部记录插入完成为止。
插入排序非常类似于整扑克牌

示例一:
source = [9, 1, 22, 31, 45, 3, 6, 2, 11] loop_count = 0 for j in range(len(source)): # 循环n次 current_val = source[j] # 先记下来每次大循环走到的第几个元素的值 position = j # 当前元素的左边的紧靠的元素比它大,要把左边的元素一个一个的往右移一位,给当前这个值插入到左边挪一个位置出来 while position > 0 and source[position - 1] > current_val: source[position] = source[position - 1] position -= 1 # 只一次左移只能把当前元素一个位置 ,还得继续左移只到此元素放到排序好的列表的适当位置 为止 loop_count += 1 # 已经找到了左边排序好的列表里不小于current_val的元素的位置,把current_val放在这里 source[position] = current_val print(source) print("loop times>>>>>>", loop_count) # 18 print("data_set>>>>>", source)
# 更容易理解的版本 data_set = [9, 1, 22, 9, 31, -5, 45, 3, 6, 2, 11] loop_count = 0 for i in range(len(data_set)): #position = i while i > 0 and data_set[i] < data_set[i - 1]: # 右边小于左边相邻的值 tmp = data_set[i] data_set[i] = data_set[i - 1] data_set[i - 1] = tmp i -= 1 loop_count += 1 print("loop times>>>>>>", loop_count) # 27 print("data_set>>>>>", data_set)
示例2:
默认从第1个元素32有序列的
alist = [32, 20, 8, 1, 99, 98, 200, 299]
拿第2个元素20同左边的有序序列(从后往前)依次比较,插入到比它小,比它大的元素中间;当然如果比最后一个元素大,就插入到最后,如果比第一个元素小,就插入到最前面。
alist = [20, 32, 8, 1, 99, 98, 200, 299]
依次拿第3个元素8同左边的有序序列(从后往前)依次比较,结果插入到最前面。
alist = [8, 20, 32, 1, 99, 98, 200, 299]
以此类推,拿右边的剩余的元素同左边的有序序列比较,插入到左边有序序列中。
代码表示:
alist = [32, 20, 8, 1, 99, 98, 200, 299] def insert_sort(alist): n = len(alist) # 外层循环:循环右边列表,第2个元素20开始到最后一个元素299 # 外层循环次数:n - 1 for i in range(1, n): # 内层循环:循环左边的有序序列 # 内层循环次数是动态的:次数为i-1 while i > 0: # range(i, 0, -1) if alist[i] < alist[i-1]: alist[i], alist[i-1] = alist[i-1], alist[i] i -= 1 else: break
4.希尔排序(shell sort):
时间复杂度:不稳定,平均O(n*log2n)~O(n*n),最优O(n**1.3),最坏O(n*n)
辅助空间:O(1)
希尔排序(Shell Sort)是插入排序的一种。
也称缩小增量排序,是直接插入排序算法的一种更高效的改进版本。
该方法的基本思想是:先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。
因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时间效率比直接插入排序有较大提高
首先要明确一下增量的取法:
第一次增量的取法为: d=count/2;
第二次增量的取法为: d=(count/2)/2;
最后一直到: d=1;
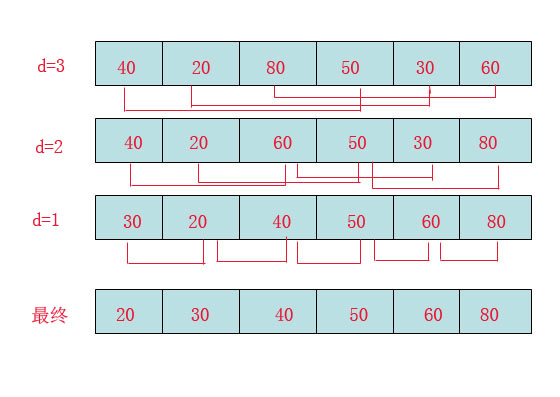
看上图观测的现象为:
d=3时:将40跟50比,因50大,不交换。
将20跟30比,因30大,不交换。
将80跟60比,因60小,交换。
d=2时:将40跟60比,不交换,拿60跟30比交换,此时交换后的30又比前面的40小,又要将40和30交换,如上图。
将20跟50比,不交换,继续将50跟80比,不交换。
d=1时:这时就是前面讲的插入排序了,不过此时的序列已经差不多有序了,所以给插入排序带来了很大的性能提高。
示例一:
import time,random #source = [8, 6, 4, 9, 7, 3, 2, -4, 0, -100, 99] #source = [92, 77, 8,67, 6, 84, 55, 85, 43, 67] source = [ random.randrange(10000+i) for i in range(10000)] #print(source) step = int(len(source)/2) #分组步长 t_start = time.time() while step >0: print("---step ---", step) #对分组数据进行插入排序 for index in range(0,len(source)): if index + step < len(source): current_val = source[index] #先记下来每次大循环走到的第几个元素的值 if current_val > source[index+step]: #switch source[index], source[index+step] = source[index+step], source[index] step = int(step/2) else: #把基本排序好的数据再进行一次插入排序就好了 for index in range(1, len(source)): current_val = source[index] # 先记下来每次大循环走到的第几个元素的值 position = index while position > 0 and source[ position - 1] > current_val: # 当前元素的左边的紧靠的元素比它大,要把左边的元素一个一个的往右移一位,给当前这个值插入到左边挪一个位置出来 source[position] = source[position - 1] # 把左边的一个元素往右移一位 position -= 1 # 只一次左移只能把当前元素一个位置 ,还得继续左移只到此元素放到排序好的列表的适当位置 为止 source[position] = current_val # 已经找到了左边排序好的列表里不小于current_val的元素的位置,把current_val放在这里 print(source) t_end = time.time() - t_start print("cost:",t_end)
示例二:

def shell_sort(alist): n = len(alist) gap = n // 2 # gap执行的次数:gap从n//2变化到1的循环 while gap > 0: # 与普通的插入算法一样,区别:普通的插入算法步长可以看作1, 希尔算法可以看作步长为gap for j in range(gap, n): # j: [gap, gap+1, gap+2, gap+3......n-1] i = j while i > 0: if alist[i] < alist[i-gap]: alist[i], alist[i-gap] = alist[i-gap], alist[i] i -= gap else: break # 逐步缩短gap步长 gap //= 2 return alist print(shell_sort([92, 77, 8, 67, 6, 84, 55, 85, 43, 67])) # 当gap没有循环,只执行一次gap=1时,是最坏情况,效率是O(n*n),这种情况相当于普通的插入算法 # gap取哪些值是最优的,需要数学算法确定。这里暂且取列表长度的对半,不断的对半,直到gap为0为止。
5.快速排序:
时间复杂度:不稳定,平均O(n*log2n),最优O(n*log2n),最坏O(n*n)
辅助空间:O(log2n)~O(n)
设要排序的数组是A[0]……A[N-1],首先任意选取一个数据(通常选用数组的第一个数)作为关键数据,
然后将所有比它小的数都放到它前面,所有比它大的数都放到它后面,这个过程称为一趟快速排序。
值得注意的是,快速排序不是一种稳定的排序算法,也就是说,多个相同的值的相对位置也许会在算法结束时产生变动
示例一:
loop_count = 0
def quick_sort(array, left, right):
'''
:param array:
:param left: 列表的第一个索引
:param right: 列表最后一个元素的索引
:return:
'''
if left >= right:
return
low = left
high = right
key = array[low] # 第一个值
while low < high: # 只要左右未遇见
global loop_count
loop_count += 1
while low < high and array[high] > key: # 找到列表右边比key大的值 为止
high -= 1
loop_count += 1
# 此时直接 把key(array[low]) 跟 比它大的array[high]进行交换
array[low] = array[high]
array[high] = key
while low < high and array[low] <= key: # 找到key左边比key大的值,这里为何是<=而不是<呢?你要思考。。。
low += 1
loop_count += 1
# array[low] =
# 找到了左边比k大的值 ,把array[high](此时应该刚存成了key) 跟这个比key大的array[low]进行调换
array[high] = array[low]
array[low] = key
quick_sort(array, left, low - 1) # 最后用同样的方式对分出来的左边的小组进行同上的做法
quick_sort(array, low + 1, right) # 用同样的方式对分出来的右边的小组进行同上的做法
# array = [96, 14, 10, 9, 6, 99, 16, 5, 1, 3, 2, 4, 1, 13, 26, 18, 2, 45, 34, 23, 1, 7, 3, 22, 19, 2]
array = [9, 1, 22, 9, 31, -5, 45, 3, 6, 2, 11]
print("before sort:", array)
quick_sort(array, 0, len(array) - 1)
print("-------final -------")
print("loop count>>>>>>>>", loop_count) # 37
print(array)
示例二:
快排,不再分左右序列。
版本一:
默认拿出第1个元素,在剩余元素中有两个指针,假设左边是比较小的指针,从第2个元素开始,右边是比较大的指针,从最后一个元素开始。
左、右指针同时移动。
左边比较:在序列中从左往右开始比较,假如比第1个元素小,指针继续往右走;否则指针暂停。
右边比较:在序列中从右往左开始比较,假如比第1个元素大,指针继续往左走;否则指针暂停。
当左右指针都暂停的时侯,交换这两个元素的位置,继续比较,直到左右指针重合。
左右指针重合的位置前面就是第1个元素应该存放的位置;此时,此位置左边的元素都比第1个元素小,此位置右边的元素都比第1个元素大。
然后,左、右两边的序列,再重复上面的过程,直到所有元素比较完成。
版本二:
现在左指针从第1个元素开始。右指针还是从最后一个开始。
将第1个元素的值赋值给一个中间变量mid_value,可以认为此时左指针对就应的是一个空值。
先移动右指针,同中间值比较:如果比中间值大,继续往左移;否则,将此值赋值给low指针所在的位置,同时暂停右指针。此时可以认为右指针指向为空。
当右指针暂停后,才开始左指针右移:如果比中间值小,继续右移;否则,将此值赋值给high指针所在位置,同时暂停这左指针。此时可以认为左指针指向为空。
当左右指针重合,第一次循环结束:将中间值插入到重合位置的前面,此时重合位置左边的值都比中间值小,右边的值都比中间值大。
然后,左边、右边的序列分别重复上面的过程,直到所有元素比较完成。
6.归并算法,稳定的O(n *log2(n)),但有空间上的额外开销:
时间复杂度:稳定,平均O(n*log2n),最优O(n*log2n),最坏O(n*log2n)
辅助空间:O(n)
先拆分,后合并:拆分的时侯,一直拆到1个元素为一个序列;合并的顺序刚好相反。
依次执行的代码:

归并排序的 代码:
def merge_sort(alist): """归并排序""" n = len(alist) if n <= 1: return alist mid = n // 2 # left、right就归并排序后的有序部分---新的列表 left_li = merge_sort(alist[:mid]) right_li = merge_sort(alist[mid:]) # 将两个有序的子序列,合并为一个新的序列 left_pointer, right_pointer = 0, 0 result = [] # 比较大小部分 while left_pointer < len(left_li) and right_pointer < len(right_li): if left_li[left_pointer] <= right_li[right_pointer]: result.append(left_li[left_pointer]) left_pointer += 1 else: result.append(right_li[right_pointer]) right_pointer += 1 # 比较后剩余部分 result += left_li[left_pointer:] result += right_li[right_pointer:] return result if __name__ == '__main__': li = [54, 26, 93, 17, 77, 31, 44, 55, 20] print(li) sorted_li = merge_sort(li) print(sorted_li)
二、搜索之 二分查找


上图查找的是值为4的元素:首先找到索引的中值,即索引0 + 最后一个元素的索引8 = 8,再除以2,得到中值为索引4;然后进行比较,索引4对应的值为7,要查找的值为4,因此判断出应该在索引4的左边查找;继续以上步骤查找。
二分查找的条件:必须是排序后的顺序表,支持索引,如排序后的列表
二分查找的实现:递归查找
def binary_search(alist, item): """二分查找:非递归实现,无需生成新的列表,可以始终使用最初的列表alias""" n = len(alist) if n > 0: mid = n // 2 if item == alist[mid]: return True elif item < alist[mid]: return binary_search(alist[:mid], item) else: return binary_search(alist[mid + 1:], item) return False li = [17, 20, 26, 31, 44, 54, 55, 77, 93] print(binary_search(li, 55)) print(binary_search(li, 17)) print(binary_search(li, 93)) print(binary_search(li, 200))
二分查找的实现:非递归,循环查找
def binary_search(alist, item): """二分查找:非递归实现,无需生成新的列表,可以始终使用最初的列表alias""" if not alist: return False n = len(alist) if n > 0: first = 0 last = n - 1 while first <= last: mid = (first + last) // 2 if item == alist[mid]: return True elif item < alist[mid]: # 不能包括mid元素 last = mid - 1 else: first = mid + 1 return False li = [17, 20, 26, 31, 44, 54, 55, 77, 93] print(binary_search(li, 55)) print(binary_search(li, 17)) print(binary_search(li, 93)) print(binary_search(li, 200))
二分查找的时间复杂度:最优O(1),最坏O(log2n)
https://space.bilibili.com/248341496/video?tid=0&page=3&keyword=&order=pubdate
posted on 2018-01-06 12:29 myworldworld 阅读(234) 评论(0) 收藏 举报





 浙公网安备 33010602011771号
浙公网安备 33010602011771号