五、DQN算法

1 简介

当状态或动作的数量非常庞大甚至连续时，可以认为状态动作对（state-action pair）是无限的，此时，我们无法用表格的形式（Q_table）来表示各个状态动作对的 action value。那么就需要用函数拟合的方法来估计 \(q(s,a)\)，即将这个复杂的 \(q\) 值表格视作数据，使用一个参数化的函数来拟合这些数据。显然，这种函数拟合的方法存在一定的精度损失，因此被称为近似方法。本章中的 DQN 算法就是用来解决连续状态下的离散动作问题的。

2 CartPole 环境

如图所示，就是一个状态值连续，动作值离散的车杆（CartPole）环境。

在车杆环境中，有一辆小车，智能体的任务是通过左右移动保持车上的杆竖直，若杆的倾斜度数过大，或者车子离初始位置左右的偏离程度过大，或者坚持时间到达 200 帧，则游戏结束。智能体的状态是一个维数为 4 的向量，每一维都是连续的，其动作是离散的，动作空间大小为 2，详情参见下表。在游戏中每坚持一帧，智能体能获得分数为 1 的奖励，坚持时间越长，则最后的分数越高，坚持 200 帧即可获得最高的分数。
状态空间

维度	意义	最小值	最大值
0	车的位置	-2.4	2.4
1	车的速度	-INF	INF
2	杆的角度	~-41.8°	~41.8°
3	杆尖端的速度	-INF	INF

动作空间

标号	动作
0	向左移动小车
1	向右移动小车

3 DQN 算法

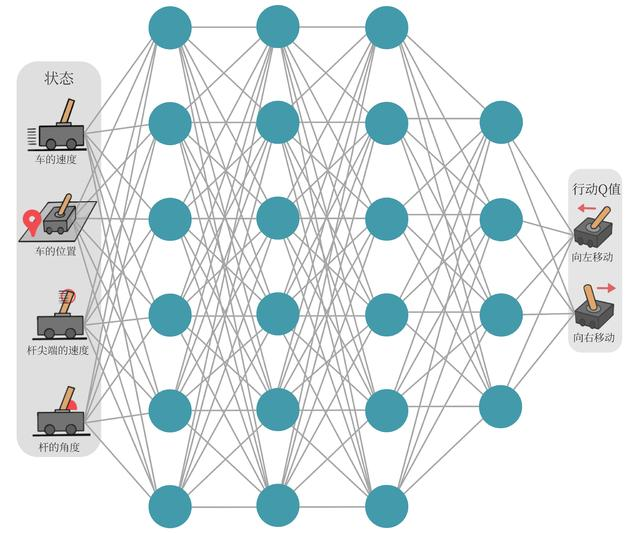
现在我们想在类似CartPole的环境中得到每个状态动作对的 \(q(s,a)\)，由于车的状态是连续的，无法用表格进行记录，因此借助函数拟合（function approximation）的思想，用一条函数来表示之。考虑到神经网络强大的表达能力，我们借助神经网络拟合函数 \(Q(s,a)\)，输入状态 \(s\) 和动作 \(a\)，输出 action value，即 \(q(s,a)\)。
通常 DQN（以及Q-learning）只能处理动作离散的情况，因为在函数的更新过程中有 \(\underset{a}{\max}\) 这一操作，因此我们可以仅输入状态 s，使其同时输出每个动作的 \(q\) 值。
假设神经网络用来拟合函数的参数为 ω，则可以将 q 值表示为 \(Q_ω(s,a)\)。我们将用于拟合 Q 函数的神经网络称为 Q 网络，如下图所示。

对于 Q 函数的损失函数，已知 Q-learning 的更新规则：

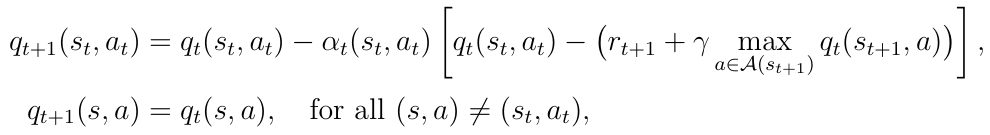
很自然地，将损失函数构造成均方误差的形式：

\[ω^*=argmin_ω\frac{1}{2N}\sum_{i=1}^{N}[q_ω(s_i,a_i)-(r_i+γ\underset{a'}{max}q_ω(s'_i,a'))]^2，a' \in \mathcal{A(s')} \]

至此，我们就可以将 Q-learning 扩展到神经网络形式——深度 Q 网络（deep Q network，DQN）算法。由于 DQN 是离线策略算法，因此我们在收集数据的时候可以使用一个 \(ε\)-greedy 策略来平衡探索与利用，将收集到的数据存储起来，在后续的训练中使用。DQN 中还有两个非常重要的模块——经验回放和目标网络，它们能够帮助 DQN 取得稳定、出色的性能。

3.1 经验回放

在原来的 Q-learning 算法中，每一个数据只会用来更新一次 \(Q\) 值。为了更好地将 Q-learning 和深度神经网络结合，DQN 算法采用了经验回放（experience replay）方法，具体做法为维护一个回放缓冲区，将每次从环境中采样得到的四元组数据（状态、动作、奖励、下一状态）存储到回放缓冲区中，训练 \(Q\) 网络的时候再从回放缓冲区中随机采样若干数据来进行训练。这么做可以起到以下两个作用：（1）满足独立假设，打破样本之间的相关性；（2）提高样本效率。

3.2 目标网络

已知我们的目标是最小化下面的目标函数：

\[[q_ω(s_i,a_i)-(r_i+γ\underset{a'}{max}q_ω(s'_i,a'))]^2，a' \in \mathcal{A(s')} \]

因此想到使用梯度下降的方法进行优化。
考虑到函数本身就包含神经网络的输出，因此在更新网络参数的同时目标也在不断地改变，这非常容易造成神经网络训练的不稳定性。举个例子，对于某一状态-动作对 \((s,a)\)，计算一次 \(q_ω(s,a)\) 后立马更新参数 \(ω\)，造成的结果就是等下一次还遇到 \((s,a)\) 时，更新的目标就不再是之前的了，而由新参数下的 \(q_{ω'}(s,a)\) 来决定，这种“移动目标”不利于训练的稳定性。为了解决这一问题，DQN 便使用了目标网络（target network）的思想：既然训练过程中 Q 网络的不断更新会导致目标不断发生改变，不如暂时先将 TD 目标中的 Q 网络固定住。为了实现这一思想，我们需要利用两套 Q 网络：
（1）训练网络 \(q_ω(s,a)\)：使用正常的梯度下降方法进行更新。
（2）目标网络 \(r+γmaxq_{ω_T}(s,a)\)：\(ω_T\) 表示网络参数。目标网络使用训练网络中一套较旧的参数，训练网络在训练的每一步都会更新，而目标网络的参数每隔 C 步才会与训练网络同步一次，即 \(ω \leftarrow ω_T\)。这样使得目标网络相对于训练网络更加稳定。

3.3 代码

我们采用的测试环境是 CartPole-v1，其状态空间相对简单，只有 4 个变量，因此网络结构的设计也相对简单：采用一层 128 个神经元的全连接并以 ReLU 作为激活函数。当遇到更复杂的诸如以图像作为输入的环境时，我们可以考虑采用深度卷积神经网络。
我们将会用到 rl_utils 库，它包含一些专门准备的函数，如绘制移动平均曲线、计算优势函数等，不同的算法可以一起使用这些函数。rl_utils 库请参考 rl_utils.py 文件。

rl_utils.py

from tqdm import tqdm
import numpy as np
import torch
import collections
import random

class ReplayBuffer:
    def __init__(self, capacity):
        self.buffer = collections.deque(maxlen=capacity) 

    def add(self, state, action, reward, next_state, done): 
        self.buffer.append((state, action, reward, next_state, done)) 

    def sample(self, batch_size): 
        transitions = random.sample(self.buffer, batch_size)
        state, action, reward, next_state, done = zip(*transitions)
        return np.array(state), action, reward, np.array(next_state), done 

    def size(self): 
        return len(self.buffer)

def moving_average(a, window_size):
    cumulative_sum = np.cumsum(np.insert(a, 0, 0)) 
    middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size
    r = np.arange(1, window_size-1, 2)
    begin = np.cumsum(a[:window_size-1])[::2] / r
    end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]
    return np.concatenate((begin, middle, end))

def train_on_policy_agent(env, agent, num_episodes):
    return_list = []
    for i in range(10):
        with tqdm(total=int(num_episodes/10), desc='Iteration %d' % i) as pbar:
            for i_episode in range(int(num_episodes/10)):
                episode_return = 0
                transition_dict = {'states': [], 'actions': [], 'next_states': [], 'rewards': [], 'dones': []}
                state = env.reset()
                done = False
                while not done:
                    action = agent.take_action(state)
                    next_state, reward, done, _ = env.step(action)
                    transition_dict['states'].append(state)
                    transition_dict['actions'].append(action)
                    transition_dict['next_states'].append(next_state)
                    transition_dict['rewards'].append(reward)
                    transition_dict['dones'].append(done)
                    state = next_state
                    episode_return += reward
                return_list.append(episode_return)
                agent.update(transition_dict)
                if (i_episode+1) % 10 == 0:
                    pbar.set_postfix({'episode': '%d' % (num_episodes/10 * i + i_episode+1), 'return': '%.3f' % np.mean(return_list[-10:])})
                pbar.update(1)
    return return_list

def train_off_policy_agent(env, agent, num_episodes, replay_buffer, minimal_size, batch_size):
    return_list = []
    for i in range(10):
        with tqdm(total=int(num_episodes/10), desc='Iteration %d' % i) as pbar:
            for i_episode in range(int(num_episodes/10)):
                episode_return = 0
                state = env.reset()
                done = False
                while not done:
                    action = agent.take_action(state)
                    next_state, reward, done, _ = env.step(action)
                    replay_buffer.add(state, action, reward, next_state, done)
                    state = next_state
                    episode_return += reward
                    if replay_buffer.size() > minimal_size:
                        b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
                        transition_dict = {'states': b_s, 'actions': b_a, 'next_states': b_ns, 'rewards': b_r, 'dones': b_d}
                        agent.update(transition_dict)
                return_list.append(episode_return)
                if (i_episode+1) % 10 == 0:
                    pbar.set_postfix({'episode': '%d' % (num_episodes/10 * i + i_episode+1), 'return': '%.3f' % np.mean(return_list[-10:])})
                pbar.update(1)
    return return_list


def compute_advantage(gamma, lmbda, td_delta):
    td_delta = td_delta.detach().numpy()
    advantage_list = []
    advantage = 0.0
    for delta in td_delta[::-1]:
        advantage = gamma * lmbda * advantage + delta
        advantage_list.append(advantage)
    advantage_list.reverse()
    return torch.tensor(advantage_list, dtype=torch.float)

主体代码

一个很重要的点是，代码中的 Q_net 类，或者说"self.q_net(states)"、"self.target_q_net(next_states)"的返回值是一个形状为(batch_size,action_space) 的二维张量（可视为一个矩阵），其值为 action_value，即 q 值。其中，batch_size 为批次大小，也就是一次迭代所使用的样本数量，通常是从经验回放缓存（ReplayBuffer类）中随机选择的一组转移，这与我们代码中的"batch_size"是一致的，是个超参数；action_space 为动作空间大小，定义了 agent 所执行的所有可能的动作，取决于环境本身，在本章中是由 gym 库的 CartPole-v1 环境定义的。例如本章中，考虑到 batch_size=64，action_space=2，返回值就应该长这样：

\[\begin{bmatrix} q_{0,0}&q_{0,1}\\ q_{1,0}&q_{1,1}\\ ...&...\\ q_{63,0}&q_{63,1}\\ \end{bmatrix} \]

import random
import gym
import numpy as np
import collections
from tqdm import tqdm
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
import rl_utils

class ReplayBuffer:
    ''' 经验回放池 '''
    def __init__(self, capacity):
        self.buffer = collections.deque(maxlen=capacity)  # 队列,先进先出

    def add(self, state, action, reward, next_state, done):  # 将数据加入buffer
        self.buffer.append((state, action, reward, next_state, done))

    def sample(self, batch_size):  # 从buffer中采样数据,数量为batch_size
        transitions = random.sample(self.buffer, batch_size)
        # 将transitions解包,然后将同一位置的元素聚合为一个tuple,
        # 因此会得到一个包含所有第一个元素的元组（state）,包含所有第二元素的元组（action）...
        state, action, reward, next_state, done = zip(*transitions)
        return np.array(state), action, reward, np.array(next_state), done

    def size(self):  # 目前buffer中数据的数量
        return len(self.buffer)

class Qnet(torch.nn.Module):
    ''' 只有一层隐藏层的Q网络 '''
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(Qnet, self).__init__()
        # 定义两个全连接层fc1和fc2
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)  # 接受state_dim个输入,有hidden_dim个输出
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)

    # 前向传播
    def forward(self, x):
        x = F.relu(self.fc1(x))  # 隐藏层使用ReLU激活函数
        return self.fc2(x)  # 输出动作的估计值

class DQN:
    ''' DQN算法 '''
    def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma,
                 epsilon, target_update, device):
        self.action_dim = action_dim
        # Q网络（训练网络）
        self.q_net = Qnet(state_dim, hidden_dim, self.action_dim).to(device)
        # 目标网络
        self.target_q_net = Qnet(state_dim, hidden_dim, self.action_dim).to(device)
        # 使用Adam优化器
        self.optimizer = torch.optim.Adam(self.q_net.parameters(), lr=learning_rate)
        self.gamma = gamma  # 折扣因子
        self.epsilon = epsilon  # epsilon-贪婪策略
        self.target_update = target_update  # 目标网络更新频率
        self.count = 0  # 计数器,记录更新次数
        self.device = device

    def take_action(self, state):  # epsilon-贪婪策略采取动作
        if np.random.random() < self.epsilon:
            action = np.random.randint(self.action_dim)
        else:
            # 将state转换成PyTorch下的张量（tensor）形式
            state = torch.tensor(np.array([state]), dtype=torch.float).to(self.device)
            # 表示在当前state下,能获取最大q值的action,item()将tensor转到Python的标量
            action = self.q_net(state).argmax().item()
        return action

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)
        rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)

        # .q_net(states)会计算出一批状态states下每个可能动作的q值,是一个张量
        # .gather(1,actions)的1表示会从第二个维度（动作空间）中选取动作为actions的q值
        q_values = self.q_net(states).gather(1, actions)  # 当前状态的Q值
        # target_q_net(next_states).max(1)会返回每个状态的可能动作的最大q值及其索引,用[0]取最大q值
        max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1)  # 下个状态的最大Q值
        q_targets = rewards + self.gamma * max_next_q_values * (1 - dones)  # TD误差目标
        dqn_loss = torch.mean(F.mse_loss(q_values, q_targets))  # 均方误差损失函数,再取均值
        self.optimizer.zero_grad()  # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
        dqn_loss.backward()  # 反向传播更新参数
        self.optimizer.step()  # 根据梯度更新神经网络参数,一般为参数=参数-学习率*梯度

        # 更新目标网络
        if self.count % self.target_update == 0:
            # state_dict()获取训练神经网络参数ω,load_state_dict()加载到目标网络
            self.target_q_net.load_state_dict(
                self.q_net.state_dict())  
        self.count += 1

lr = 2e-3
num_episodes = 500
hidden_dim = 128
gamma = 0.98
epsilon = 0.01
target_update = 10
buffer_size = 10000
minimal_size = 500
batch_size = 64
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")

env_name = 'CartPole-v1'
env = gym.make(env_name, new_step_api=True)
random.seed(0)
np.random.seed(0)
env.reset(seed=0)
torch.manual_seed(0)
replay_buffer = ReplayBuffer(buffer_size)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon, target_update, device)

return_list = []
for i in range(10):
    with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
        for i_episode in range(int(num_episodes / 10)):
            episode_return = 0
            state = env.reset()
            done = False
            while not done:
                action = agent.take_action(state)
                next_state, reward, terminated, truncated, _ = env.step(action)
                if terminated or truncated:
                    done = True
                replay_buffer.add(state, action, reward, next_state, done)
                state = next_state
                episode_return += reward
                # 当buffer数据的数量超过一定值后,才进行Q网络训练
                if replay_buffer.size() > minimal_size:
                    # 利用经验回放池采样
                    b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
                    transition_dict = {
                        'states': b_s,
                        'actions': b_a,
                        'next_states': b_ns,
                        'rewards': b_r,
                        'dones': b_d
                    }
                    agent.update(transition_dict)
            return_list.append(episode_return)
            if (i_episode + 1) % 10 == 0:
                pbar.set_postfix({
                    'episode':
                    '%d' % (num_episodes / 10 * i + i_episode + 1),
                    'return':
                    '%.3f' % np.mean(return_list[-10:])
                })
            pbar.update(1)

episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format(env_name))
plt.show()

mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format(env_name))
plt.show()

Iteration 0: 100%|█████████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 950.36it/s, episode=50, return=9.000]
Iteration 1: 100%|████████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 67.96it/s, episode=100, return=14.500]
Iteration 2: 100%|███████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:04<00:00, 12.13it/s, episode=150, return=117.500]
Iteration 3: 100%|███████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:12<00:00,  4.09it/s, episode=200, return=184.500]
Iteration 4: 100%|███████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:11<00:00,  4.37it/s, episode=250, return=195.800]
Iteration 5: 100%|███████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:13<00:00,  3.80it/s, episode=300, return=248.300]
Iteration 6: 100%|███████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:17<00:00,  2.80it/s, episode=350, return=320.300]
Iteration 7: 100%|███████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:20<00:00,  2.42it/s, episode=400, return=373.500]
Iteration 8: 100%|███████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:24<00:00,  2.06it/s, episode=450, return=393.400]
Iteration 9: 100%|███████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:22<00:00,  2.23it/s, episode=500, return=361.800]

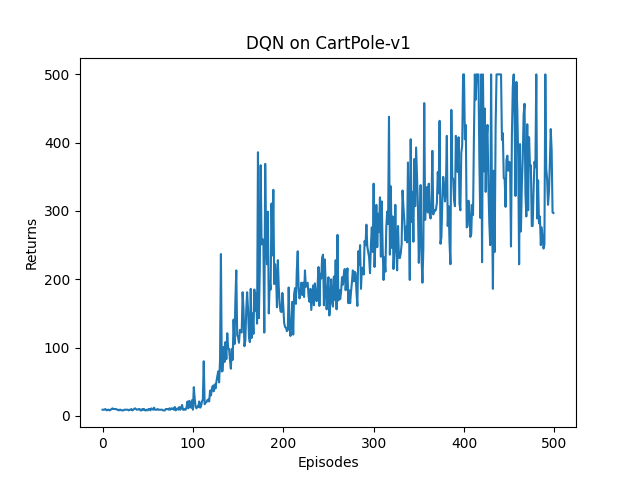
可以看到，DQN 的性能在 100 个序列后很快得到提升，但之后会持续出现一定程度的震荡，这主要是神经网络过拟合到一些局部经验数据后由运算带来的影响。