伽马函数和伽马分布[原创www.cnblogs.com/helesheng]

一、伽马函数

\(\Gamma\) 函数（Gamma Function），中文称为伽玛函数，是数学中一个非常重要的特殊函数，通常被视为阶乘概念在实数甚至复数域上的推广。\(\Gamma\) 函数是连接离散数学（阶乘）与连续分析（积分）的一座桥梁。它将“n 个数的乘积”平滑地扩展到了“任意数的乘积”。它由数学家欧拉（Leonhard Euler）首先引入。

1. 核心定义

\(\Gamma\) 函数最标准的定义是利用含参变量的广义积分给出的（称为欧拉第二积分）：

\[\Gamma(z) = \int_{0}^{\infty} t^{z-1} e^{-t} \, dt \tag 1 \]

收敛条件：
对于实数\(z\)，该积分收敛的条件是 \(z > 0\)。通过解析延拓，\(\Gamma\) 函数的定义域可以扩展到除了非正整数\(（0, -1, -2, \dots）\)以外的所有复数。

2. 与阶乘的关系（最重要的性质）

\(\Gamma\)函数最重要的性质是它与阶乘的直接联系。对于正整数 n，有：

\[\Gamma(n) = (n-1)! \tag 2 \]

也就是说，\(\Gamma(n)\) 等于 \(n-1\) 的阶乘。

\[\Gamma(1) = 0! = 1 \\ \Gamma(2) = 1! = 1\\ \Gamma(3) = 2! = 2\\ \Gamma(4) = 3! = 6\\ \]

为什么是 \((n-1)!\) 而不是 \(n!\) ？
这其实是历史遗留问题。当时的数学家（如勒让德）定义这个函数时，为了让公式在某些积分运算（如拉普拉斯变换）中形式更简洁，选择了这种移位的形式。

3.关键性质

(1) 递推公式
\(\Gamma\) 函数满足以下递推关系：

\[\Gamma(z+1) = z \cdot \Gamma(z) \tag 3 \]

这个性质对应了阶乘的递推性质 \(n! = n \cdot (n-1)!\)。
(2) \(\Gamma(\frac{1}{2})\) 的值

\[\Gamma\left(\frac{1}{2}\right) = \sqrt{\pi} \tag 4 \]

这一结果在计算正态分布的积分时非常关键。
(3) 余元公式
对于 $0 < z < 1 $的实数：

\[\Gamma(z) \Gamma(1-z) = \frac{\pi}{\sin(\pi z)} \tag 5 \]

这个公式展示了 \(\Gamma\) 函数与三角函数之间的联系。
(4) 极点
在实数轴上，当 z 趋近于 0 或负整数时，\(\Gamma(z)\) 的值趋向于无穷大（即函数在这些点有极点）。这意味着 0 和负整数的阶乘在传统意义上是未定义的。

4. 图像形状

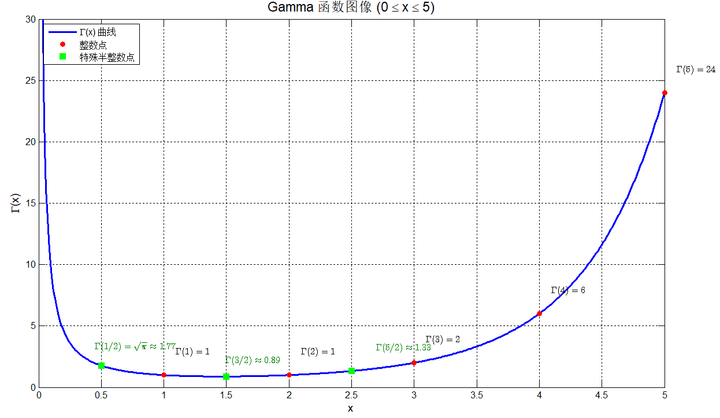
对于 \(x > 0\) 的实数部分，\(\Gamma(x)\) 的图像的特点：

• 当 \(x \to 0^+\) 时，\(\Gamma(x) \to +\infty\)。
• 在区间 $(0, +\infty) $上，函数呈“U”型，但在 x 约等于 1.4616 处有一个全局最小值，最小值约为 0.8856。
• 随着 \(x\) 增大，$\Gamma(x) $的增长速度极快，比指数函数还要快（类似于阶乘的增长）。

图1 $\Gamma$函数

5.为什么要使用 \(\Gamma\) 函数？

“已经有了$ n!$ 来计算整数乘积，为什么还需要一个复杂的积分函数？”
原因在于，现实世界中的问题不仅仅是离散的（整数），很多时候是连续的。
应用场景举例：
(1)概率统计（最重要的应用）：
正态分布：计算高斯积分时会用到$ \Gamma(1/2)$。
t分布、卡方分布、Beta分布：这些统计学中核心的概率密度函数，其归一化常数（让总面积等于1的系数）都是由 \(\Gamma\) 函数定义的。如果没有 \(\Gamma\) 函数，现代统计学的大公式将无法书写。
(2)微积分与解析数论：
它可以用来计算一些看似复杂的广义积分，例如 \(\int_{0}^{\infty} e^{-x^2} dx\)。
黎曼 \(\zeta\) 函数的研究中大量使用了 \(\Gamma\) 函数。
(3)分数阶微积分：
当你想要问“1/2 阶导数”是什么意思时，\(\Gamma\) 函数就提供了定义的数学基础。

二、\(\Gamma\)分布

\(\Gamma\) 分布（Gamma Distribution），是统计学和概率论中非常重要的连续概率分布族。
\(\Gamma\)分布的典型物理意义是描述“第\(k\)个事件发生所需的时间”：
假设公交车到达服从泊松分布，平均到达率为λ（单位时间内平均来的车辆数），也可以理解为平均到达时间为\(\theta\)。
设 \(T_k\)​ 为第 \(k\)辆车到达所需的时间（多少个单位时间）。
\(T_k\) 服从参数为 \((k,θ=\frac{1}{λ})\) 的 \(\Gamma\) 分布。

1、\(\Gamma\)分布的概率密度函数

\[f(x;k,θ)=\frac{1}{\Gamma(k)θ^k}​ x^{k−1}e^{−\frac{x}{θ}​} \tag 6 \]

\[其中x>0 \]

\(\Gamma\)分布由两个参数决定：

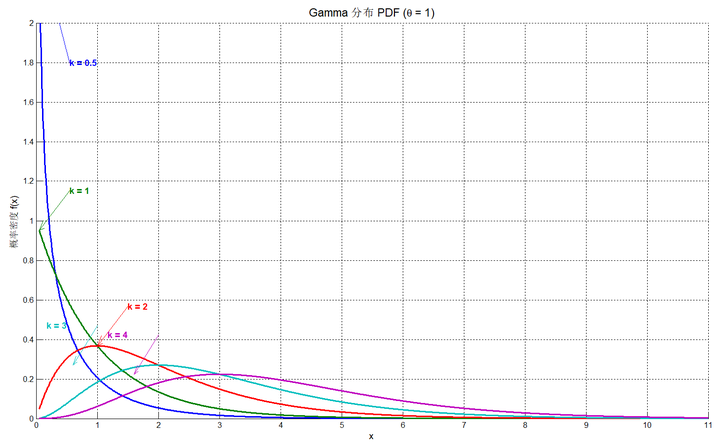
1. 形状参数 (Shape Parameter)：通常记为 \(k  (k>0)\)。它决定了分布曲线的形状（比如是单调递减还是有一个山峰），相当于等待第\(k\)辆车到达。
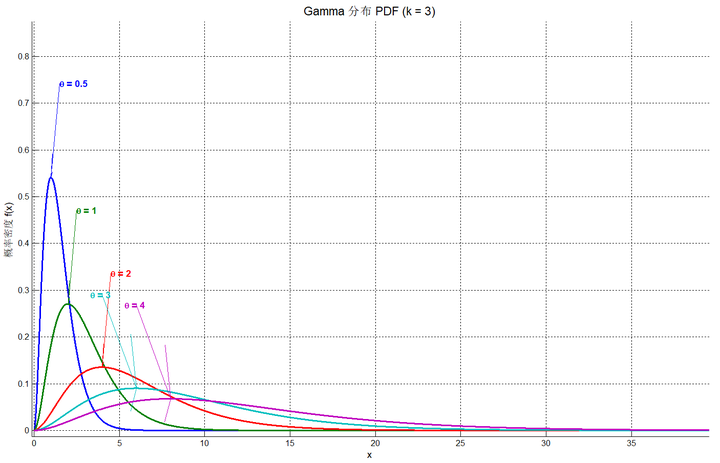
2. 尺度参数 (Scale Parameter)：通常记为 \(θ  (θ>0)\)。它决定了分布的“拉伸”程度，相当于两辆车之间间隔时间的数学期望（尺度参数）。而尺度参数\(\theta\)的倒数\(\lambda=\frac{1}{\theta}\)称为率参数，相当于单位时间内的来车数量，是另一种等价的\(\Gamma\)分布定义方式。
   其中\(\Gamma\)函数的作用是“归一化常数”。它的存在是为了保证整个概率密度函数下方的面积积分等于 1。
   如果把前面的常数项丢掉，只看\(x^{k−1}e^{−\frac{x}{θ}​}\)，你会发现它和\(\Gamma\) 函数的积分定义长得一模一样。正是因为有了 \(\Gamma\)在分母上做平衡，才使得总概率为 1。

图2 不同形状参数k（到达车数量）下的$\Gamma$分布概率密度函数 图3 不同尺度参数（间隔时间数学期望）下的$\Gamma$分布概率密度函数

2、伽马分布和泊松分布之间的关系

为了计算第\(k\)辆车到达所需的时间\(T_k\)​ ，先求\(T_k\)​ 的分布函数\(F(t)=P(T_k \leq t)\)，即第\(k\)辆车到达的时间小于\(t\)的概率，但这并不容易计算。改成计算在时间t内到达的车辆数大于k的概率，再反过来用1减去这个值就得到了\(F(t)\)。时间t内到达的车数为k的概率符合泊松分布，对泊松分布求达到数大于k的无穷级数从而得到F(t)，再对其求导就得到了(6)所示的伽马分布概率密度函数。
特别的，当k为1时到达的时间\(T_1\)服从\(\Gamma\)分布的退化——指数分布，其概率密度函数为：

\[f(x,\lambda) = \lambda e^{-\lambda x} \]

3、伽马分布和卡方分布（\(\chi^2\)）

\(\chi^2\)分布是 \(n\)个独立标准正态分布随机变量平方之和的分布。
若n个相互独立的标准正态随机变量（即服从 \(\mathbb N(0,1)\)的变量）分别为 \(Z_1,Z_2,...,Z_n\)​，则它们的平方和:

\[Q = \sum_{i=1}^{n} Z_i^2 \]

服从自由度为n 的卡方分布，记作 \(Q \sim \chi^2(n)\)。
可以证明，\(\chi ^2(n)\)分布实际是伽马分布的特例。具体说，自由度为n的\(\chi^2\)的分布，等价于形状参数为\(k=\frac{n}{2}\)，率参数\(\lambda=\frac{1}{2}\)的\(\Gamma\)分布。
通俗的说，\(\chi ^2(n)\)是等待第\(\frac{n}{2}\)辆车，且车辆到达速率为每单位时间\(\frac{1}{2}\)辆车的分布。

4、伽马分布的数字特征

1） 数学期望

描述的是分布的“中心”位置。

\[E[X] = k \theta \]

• 直观理解：如果你在等公交（\(k\) 是第几辆车，\(\theta\) 是平均每车间隔），期望就是等到第 \(k\) 辆车平均需要的时间。
  例如：$ k=3 $, \(\theta=2\)，则平均等待时间为 \(3 \times 2 = 6\)。

2） 方差

描述的是分布的“离散”程度，即数据围绕均值波动的幅度。

\[D(X) = k \theta^2 \]

• 直观理解：方差与 \(k\) 成正比，与 \(\theta\) 的平方成正比。尺度参数 \(\theta\) 对波动的影响比形状参数$ k $更大。

3）标准差

\[\sigma = \sqrt{k} \theta \]

• 注意标准差与均值的比值：\(\frac{\sigma}{E[X]} = \frac{\sqrt{k}\theta}{k\theta} = \frac{1}{\sqrt{k}}\)。
  这意味着：形状参数 \(k\) 越大，相对波动越小。当 \(k\) 很大时，数据会越来越集中在均值附近。