曼哈顿距离和切比雪夫距离
曼哈顿距离(Manhattan Distance)
解释:只能横着或竖着走,坐标上两点的距离
假设存在两点 \(A(x_1, y_1)\) \(B(x_2, y_2)\)
\(dis(A, B) = |x_1 - x_2| + |y_1 - y_2|\)
对于上方求曼哈顿距离的式子,有四种情况
\(
\begin{cases}
x_1 > x_2 & y_1 > y_2 & {d = x_1 - x_2 + y_1 - y_2 = (x_1 + y_1) - (x_2 + y_2)} \\
x_1 > x_2 & y_1 < y_2 & {d = x_1 - x_2 + y_2 - y_1 = (x_1 - y_1) - (x_2 - y_2)} \\
x_1 < x_2 & y_1 > y_2 & {d = x_2 - x_1 + y_1 - y_2 = (x_2 + y_2) - (x_1 + y_1)} \\
x_1 < x_2 & y_1 < y_2 & {d = x_2 - x_1 + y_2 - y_1 = (x_2 - y_2) - (x_1 - y_1)}
\end{cases}
\)
观察发现,上方四种情况中反复出现了两个值 \(x + y\) 和 \(x - y\)
发现对于四种情况,曼哈顿距离也就是
例题:
求到所有定点的最大曼哈顿距离最小
切比雪夫距离(Chebyshev distance)
解释:各坐标数值差绝对值的最大值

假设存在两点 \(A(x_1, y_1)\) \(B(x_2, y_2)\)
\(D_{Chess}(A, B) = max(|x_1 - x_2|,~ |y_1 - y_2|)\)
这时忽然发现,之前曼哈顿距离得出的结论
\( dis = max(|(x_1 + y_1) - (x_2 + y_2)|, ~|(x_1 - y_1) - (x_2 - y_2)|) \)
与切比雪夫距离的形式非常相似
并且如果将 A,B 两个点的坐标换成 \((x_1 + y_1, x_1 - y_1)\) 与 \((x_2 + y_2, x_2 - y_2)\)
这两个点的切比雪夫距离刚好等于 \((x_1, y_1)\) \((x_2, y_2)\) 的曼哈顿距离
那么可以得到另一个结论
由上边的结论反向推导一下
得到了
上方的例题中,正是利用了这个原理
将曼哈顿距离转为切比雪夫距离后,\(A',B'\) 的 x,y 坐标就相互独立了。
求出转化后最小和最大的 x 坐标和 y 坐标。
对于每个点算一下他们距离最小和最大的 x / y 的距离,取个max就是最远的距离。
对于将切比雪夫距离转曼哈顿距离的问题
例题:
求到所有定点的切比雪夫距离之和最小
以上,用式子推导了一下两个距离的转化关系
曼哈顿距离的计算方法,对于求和计算帮助很大
利用切比雪夫转曼哈顿的类似思想,可以解决一些这种二维的最大最小值问题
对于二元的最小值最大值常见操作就是变换成长度与绝对值之间的关系
绝对值求和则就考虑排序和前缀和操作
CF2131F
如果转化为图示,会发现
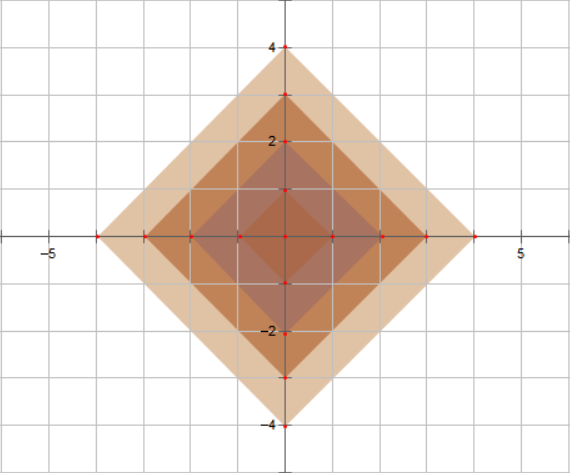
曼哈顿距离如图是一个以当前点为中心的菱形,切比雪夫距离如上图是一个当前点为中心的正方形
所以它们之间的相互转化相当于将这个图形旋转 \(45^{\circ}\)然后适当放缩
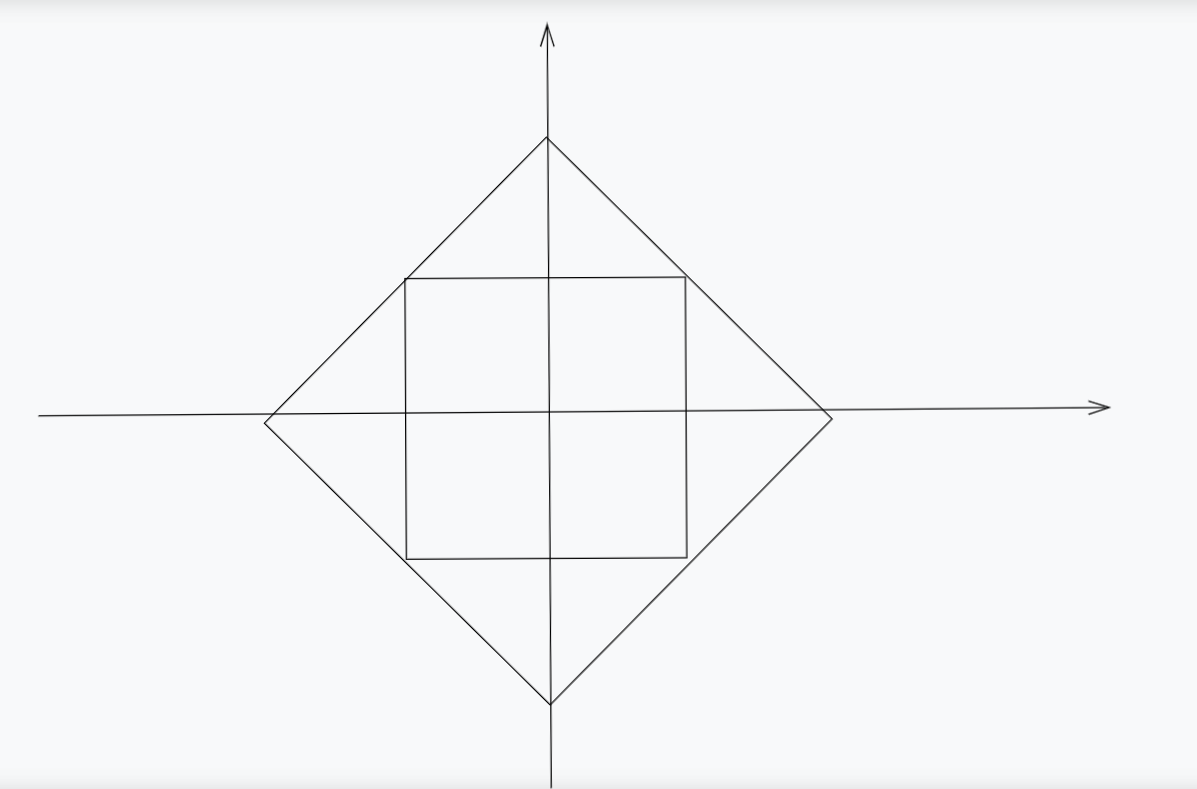
所以
曼哈顿距离转切比雪夫距离 = ①旋转\(45^{\circ}\) \(~~~~~~~~~~~\)②乘以 \(\sqrt{2}\)
切比雪夫距离转曼哈顿距离 = ①反向旋转\(45^{\circ}\) \(~~~~~\)②除以 \(\sqrt{2}\)
对于python之类的语言,直接用rotate函数之类的方式改变坐标确实比较方便
而对于 c++ 来说,就是利用之前推出的式子,就能达成类似的效果
第一步 :曼哈顿距离转切比雪夫距离
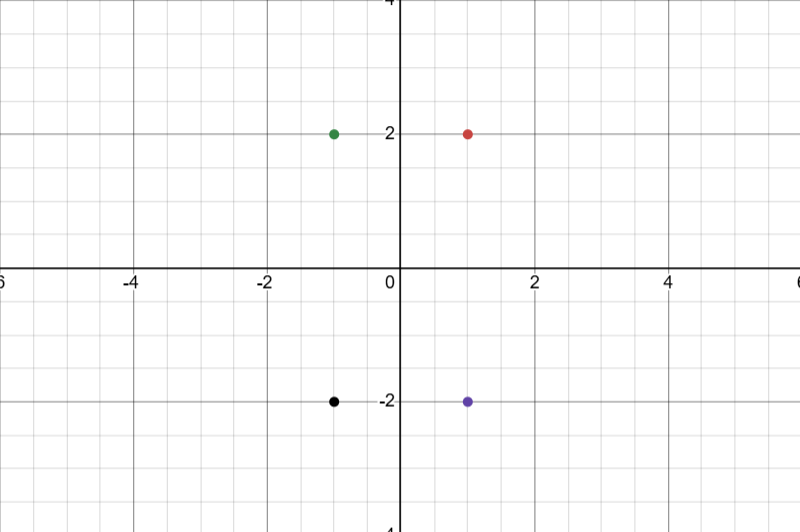
(x,y)转化为(x+y,x−y)
第二步 :切比雪夫距离转曼哈顿距离
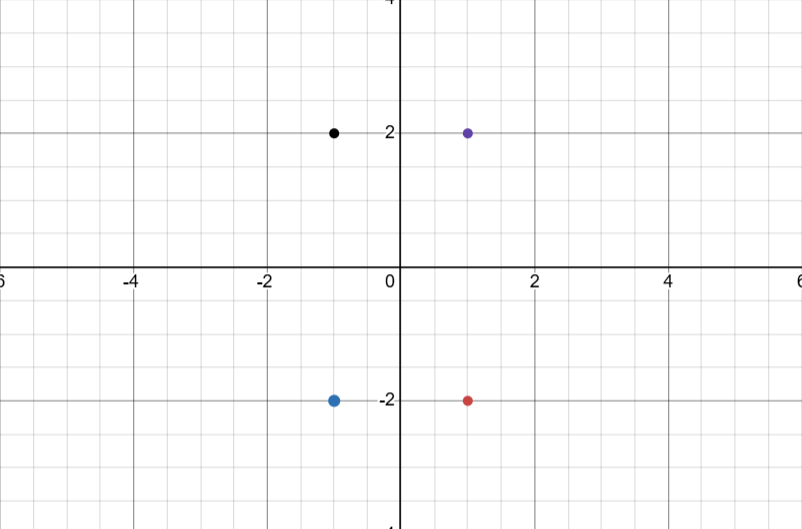
(x, y) 转化为 \((\frac{x + y}2, \frac{x - y}2)\)





 浙公网安备 33010602011771号
浙公网安备 33010602011771号