聚类和分类

聚类和分类判别有什么区别？

简单的说，聚类的分析没有学习集，而分类有学习集

1. 关键度量指标：距离（r中dist( )函数可用于算距离）

    常用距离

            绝对值距离

            欧氏距离

            闵可夫斯基距离

            切比雪夫距离

            马氏距离

            Lance和Williams距离

            离散变量的距离计算

2.动态聚类：K-means方法

    算法：

    　　1 选择K个点作为初始质心

    　　2 将每个点指派到最近的质心，形成K个簇（聚类）

    　　3 重新计算每个簇的质心 4 重复2-3直至质心不发生变化

    R中实现聚类分析的函数为kmeans( )函数

     例:

　　   

 

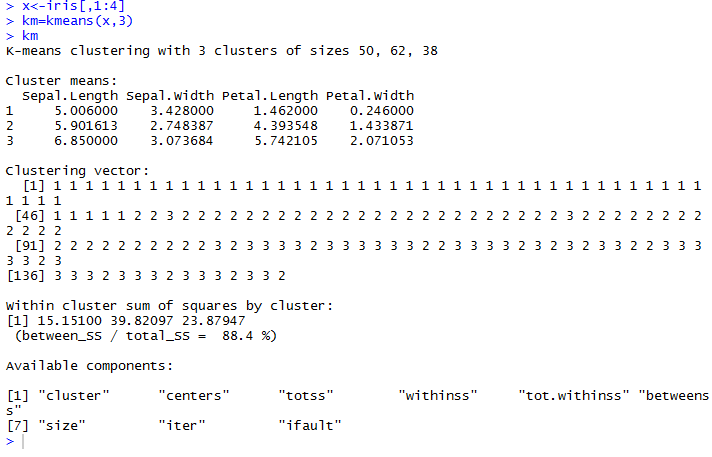
     K-means算法的优缺点

　　　 有效率，而且不容易受初始值选择的影响

　　　不能处理非球形的簇***

           不能处理不同尺寸，不同密度的簇

           离群值可能有较大干扰（因此要先剔除）***

  

3.基于有代表性的点的技术：K中心聚类法

     算法步骤

　　 1. 随机选择k个点作为“中心点”

         2 .计算剩余的点到这k个中心点的距离，每个点被分配到最近的中心点组成聚簇

         3. 随机选择一个非中心点Or，用它代替某个现有的中心点Oj，计算这个代换的总代价S

         4 .如果S<0，则用Or代替Oj，形成新的k个中心点集合

         5 重复2，直至中心点集合不发生变化

      K中心法的实现：PAM(cluster包的pam( )函数)

            PAM使用离差平方和来计算成本S（类似于ward距离的计算）

            R语言的cluster包实现了PAM

      K中心法的优点：

            对于“噪音较大和存在离群值的情况，K中心法更加健壮，不像 Kmeans那样容易受到极端数据影响

      K中心法的缺点：

            执行代价更高

 

4.基于密度的方法: DBSCAN(DBSCAN = Density-Based Spatial Clustering of Applications with Noise)

     本算法将具有足够高密度的区域划分为簇，并可以发现任何形状的聚类

     算法基本 思想

         1 指定合适的 r 和 M

         2 计算所有的样本点，如果点p的r邻域里有超过M个点，则创建一个以p为核心点的新簇

         3 反复寻找这些核心点直接密度可达（之后可能是密度可达）的点，将其加入到相应的簇 ，对于核心点发生“密度相连”状况的簇，给予合并

         4 当没有新的点可以被添加到任何簇时，算法结束   

         注：(r-邻域：给定点半径r内的区域

                 核心点：如果一个点的r-邻域至少包含最少数目M个点，则称该点为核心点

                 直接密度可达：如果点p在核心点q的r-邻域内，则称p是从q出发可以直接密度可达 如果存在点链p1 ,p2 , …, pn，p1=q，pn=p，

         pi+1是从pi关于r和M直接密度可达，则称点p 是从q关于r和M密度可达的

                 如果样本集D中存在点o，使得点p、q是从o关于 r和M密度可达的，那么点p、q是关于r 和M密度相连的)

5.主成分分析

     原理及内容：

             通过析取主成分显出最大的个别差异，也用来削减回归分析和聚类分析中变量的数目

             可以使用样本协方差矩阵或相关系数矩阵作为出发点进行分析

             成分的保留：Kaiser主张（1960）将特征值小于1的成分放弃，只保留特征值大于1的 成分

             如果能用不超过3-5个成分就能解释变异的80%，就算是成功***

             通过对原始变量进行线性组合，得到优化的指标

             把原先多个指标的计算降维为少量几个经过优化指标的计算（占去绝大部分份额）

     基本思想：设法将原先众多具有一定相关性的指标，重新组合为一组新的互相独立的 综合指标，并代替原先的指标

     主成分分析的直观几何意义：

              

 

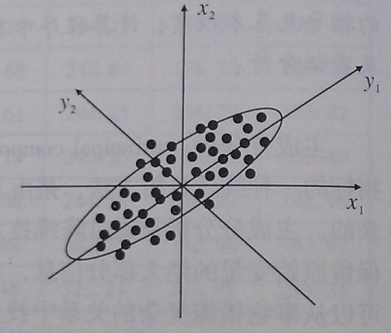
    R语言实现：princomp( )函数