J-牛牛想要成为hacker

题目链接：https://ac.nowcoder.com/acm/contest/9982/J

思路：构造长度为n的数列：
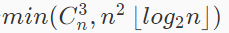,当这个公式内log是下取整时 n为27时相等，则只要在1~27的位置时间复杂度为O(n³),之后的时间复杂度为n² log₂ n,由于log（1e5）<27,则在1~27使用斐波那契构造，27之后填充1即可满足条件。

坑点：
1.斐波那契数列正好不构成三角形，两边之和等于第三边
2.后边用1填充，不构成三角形，惯性思维会想不到

反思:由于构造结果的数据范围为1e9，所以后边用等差数列构造会爆掉，思维进入牛角尖，其实只要第一个斐波那契值和后两个循环得到的值不构成三角形即可，没必要非得两边和等于第三遍。

#include<bits/stdc++.h>

using namespace std;
int a[50];
int main (){
    int n;
    cin>>n;
   a[1]=2;a[2]=3;
    for(int i=3;i<=33;i++)
     a[i]=a[i-1]+a[i-2];
    for(int i=1;i<=min(33,n);i++)
        cout<<a[i]<<" ";
    for(int i=31;i<=n;i++)
        cout<<"1 ";
    return 0;
}