导数学习笔记

基本知识

一些特殊函数的图象

\(f(x)=x\mathrm{e}^x\)

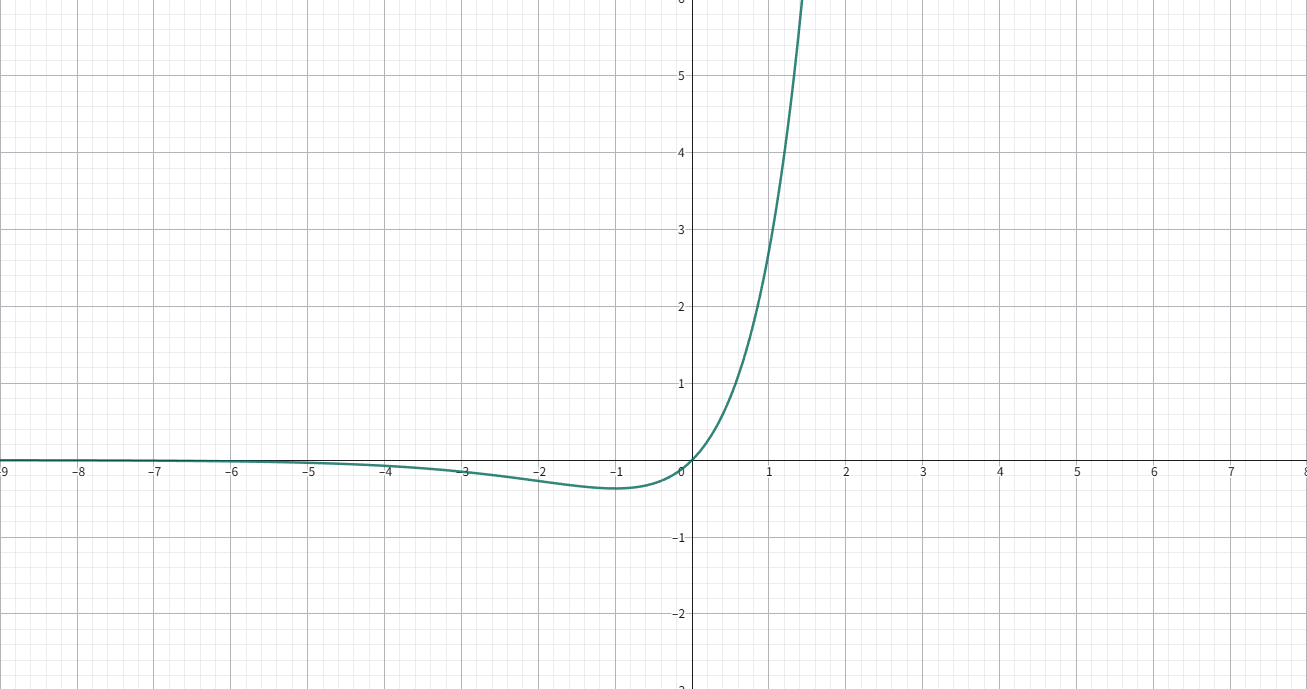
在 \(x=-1\) 处取极小值 \(f(x)=-\dfrac{1}{\mathrm{e}}\)．

---

\(f(x)=\dfrac{\mathrm{e}^x}{x}\)

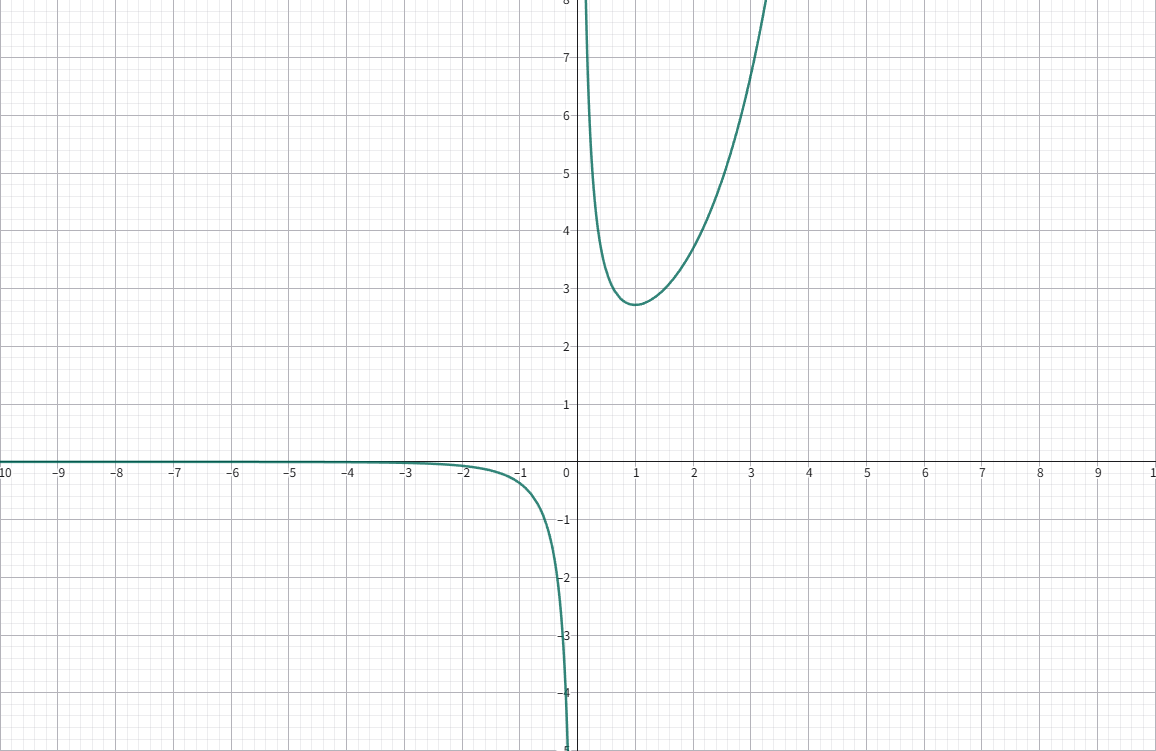
在 \(x=1\) 处取极小值 \(f(x)=\mathrm{e}\)．

---

\(f(x)=\dfrac{x}{\mathrm{e}^x}\)

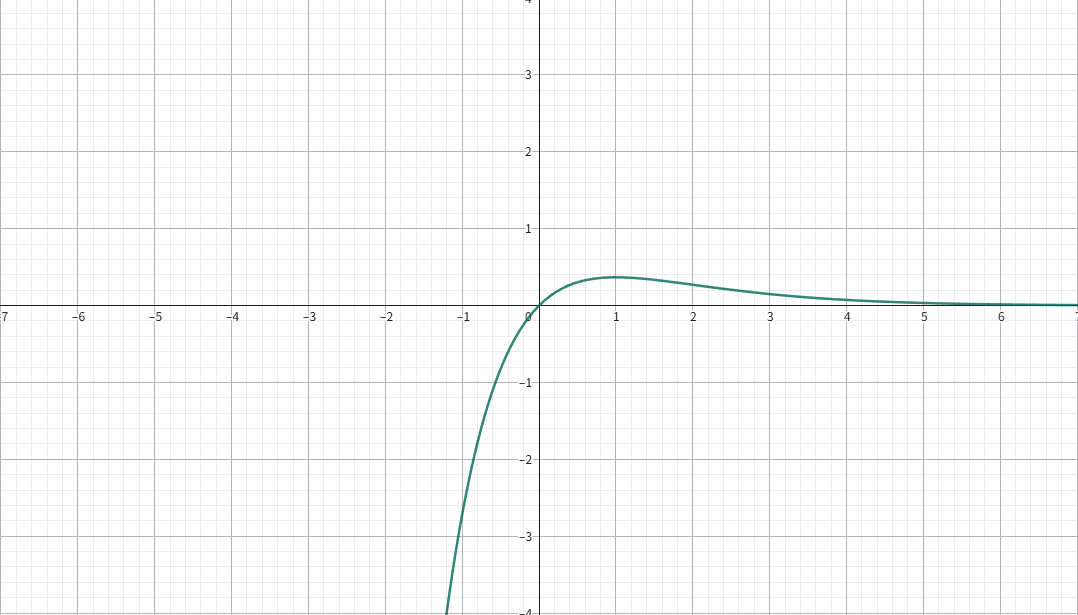
在 \(x=1\) 处取极大值 \(f(x)=\dfrac{1}{\mathrm{e}}\)．

---

\(f(x)=x\ln x\)

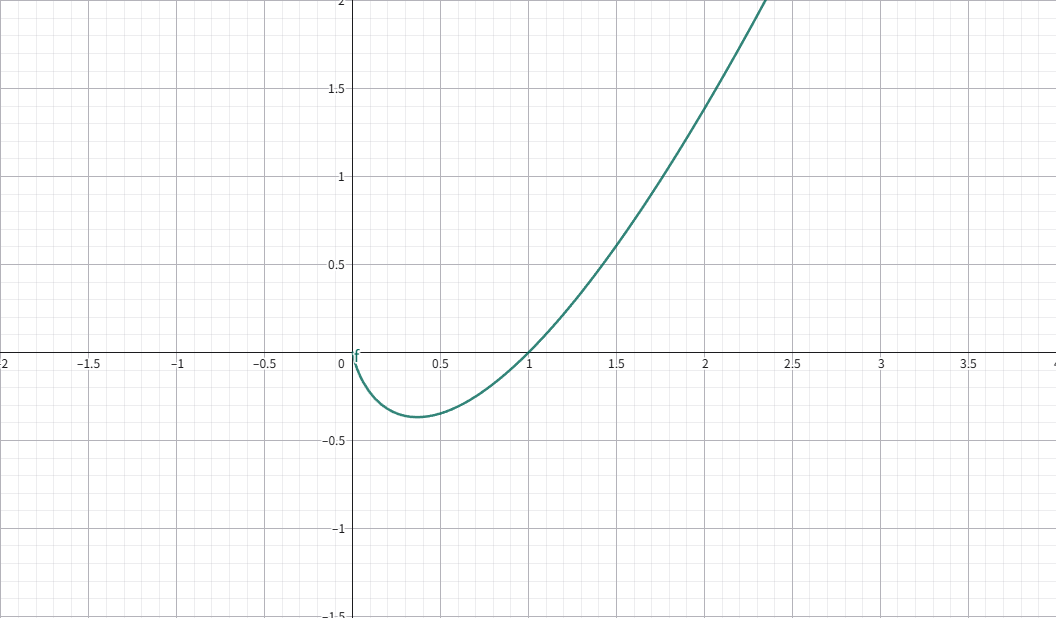
在 \(x=\dfrac{1}{\mathrm{e}}\) 处取极小值 \(f(x)=-\dfrac{1}{\mathrm{e}}\)．

---

\(f(x)=\dfrac{\ln x}{x}\)

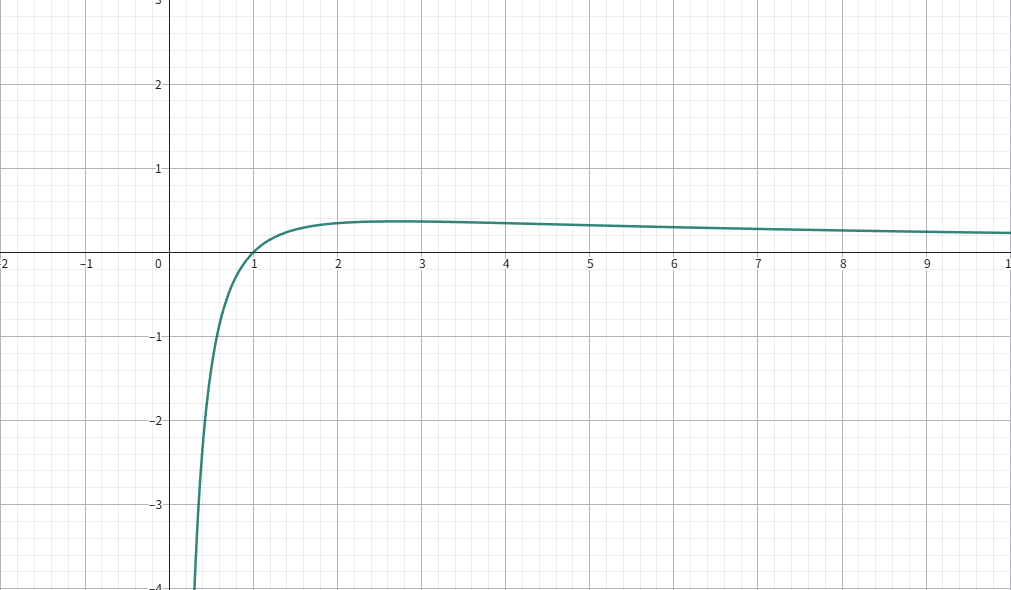
在 \(x=\mathrm{e}\) 处取极大值 \(f(x)=\dfrac{1}{\mathrm{e}}\)．

---

\(f(x)=\dfrac{x}{\ln x}\)

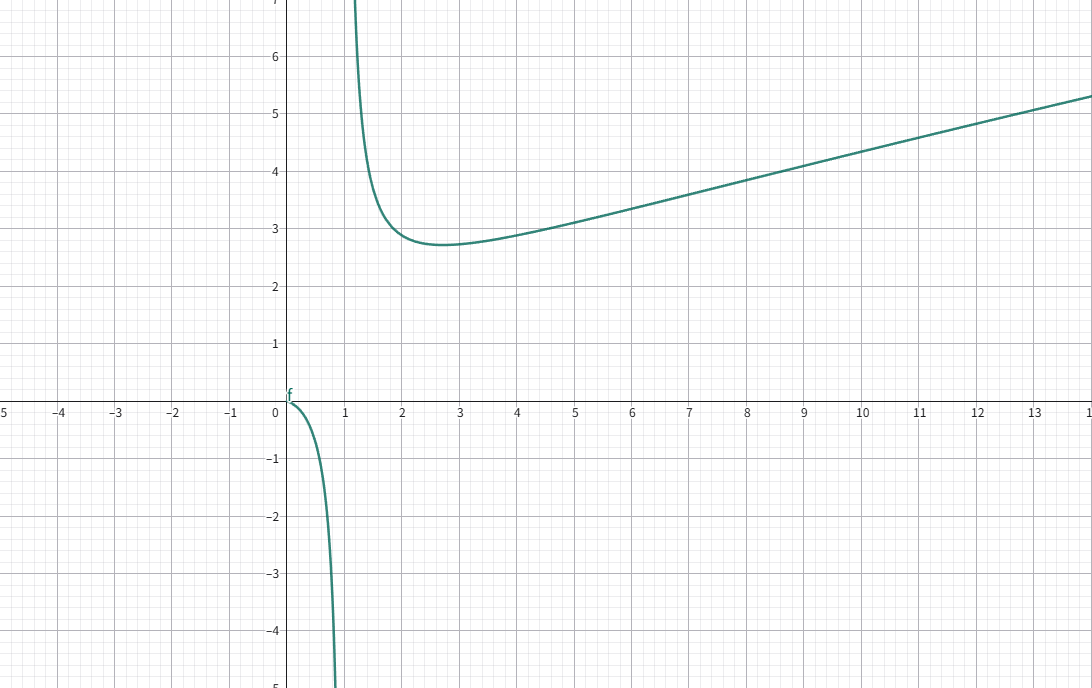
在 \(x=\mathrm{e}\) 处取极大值 \(f(x)=\mathrm{e}\)．

常用函数不等式

• \(\ln x\) 常用放缩：

  \[1-\dfrac{1}{x}\le\ln x\le x-1. \]

  在 \(x=1\) 处取等．

• \(\mathrm{e}^x\) 常用放缩：

  \[\mathrm{e}^x\ge \mathrm{e}x\\\mathrm{e}^x\ge x+1. \]

  分别在 \(x=1\) 和 \(x=0\) 处取等．

• 设 \(a>b>0\)：

  \[\sqrt{ab}<\frac{a-b}{\ln a-\ln b}<\frac{a+b}{2}. \]

猎奇题目大赏

函数极值

T1

若函数 \(f(x)=\mathrm{e}^x(x-3)-\dfrac{1}{3}kx^3+kx^2\) 只有一个极值点，求 \(k\) 的取值范围．

T2

已知 \(x=1\) 是函数 \(f(x)=\dfrac{\mathrm{e}^x}{x}-k\left(\dfrac{1}{2x^2}-\dfrac{1}{x}\right)\) 的唯一一个极值点，求实数 \(k\) 的取值范围．

函数不等式

T1

已知三次函数 \(f(x)=x^3+bx^2+cx+d\)，其导函数为 \(f'(x)\)，存在 \(t\in(1,4)\)，满足 \(f(2-t)=f(t)=f'(t)=0\)．记 \(f(x)\) 的极大值为 \(M\)，则 \(M\) 的取值范围是？

解：

由于已经知道 \(f(x)=0\) 的两根，考虑将 \(f(x)\) 写为零点式，即 \(f(x)=(x-2+t)(x-t)^2\)（因为 \(f'(t)=0\)，故在 \(x=t\) 处可以取二重根）．

则 \(f'(t)=2(x-t)(x+t-2)+(x-t)^2=(x-t)(3x+t-4)\)．

故 \(f\left(\dfrac{4-t}{3}\right)\) 是 \(f(x)\) 的极大值，故 \(M=\dfrac{32}{27}(t-1)^3\)．

故 \(M\) 的取值范围为 \((0,32)\)．

T2

已知函数 \(f(x)=\ln x+x\)，证明：\(xf(x)<\mathrm{e}^x\)．

解：

• 法一：（by @crimson000）

  据题意，即证 \(x\ln x+x^2<\mathrm{e}^x\)．根据 \(\ln x\le x-1\)，只需证 \(x(x-1)+x^2<\mathrm{e}^x\)．

  设 \(g(x)=\mathrm{e}^x-2x^2+x\)，则只需证对于所有 \(x>0\)，有 \(g(x)>0\)．

  \(g'(x)=\mathrm{e}^x-4x+1,g''(x)=\mathrm{e}^x-4\)．

  根据分析，\(g'(0)>0,g'(1)<0,g'(2)>0\)．

  设 \(g'(x)=0\) 的两根为 \(x_1,x_2\)，且 \(x_1<x_2\)．

  则有 \(x_1\in(0,1),x_2\in(1,2)\)．

  \(g(x)\) 在 \((0,x_1),(x_2,+\infty)\) 上单调递增，在 \((x_1,x_2)\) 上单调递减．

  故 \(g(x)_{\min}=\min\{g(0),g(x_2)\}\)．

  已知 \(g(0)>0\)．\(g(x_2)=-2x_2^2+5x_2-1\)，且 \(x_2\in(1,2)\)，故 \(g(x_2)>0\)，原命题成立．

• 法二：（by @Ascnbeta）

  两边同时除以 \(x^2\)，即证 \(\dfrac{\ln x}{x}+1<\dfrac{\mathrm{e}^x}{x^2}\)．

  设 \(g(x)=\dfrac{\ln x}{x}+1,h(x)=\dfrac{\mathrm{e}^x}{x^2}\)．

  则 \(g'(x)=\dfrac{1-\ln x}{x^2},h'(x)=\dfrac{(2-x)\mathrm{e}^x}{x^3}\)．

  故 \(g(x)_{\max}=g(e)=\dfrac{1}{\mathrm{e}}+1,h(x)_{\min}=h(2)=\dfrac{\mathrm{e}^2}{4}\)．

  \(g(x)_{\max}<h(x)_{\min}\)，故原命题成立．

T3

求证：当 \(0<x<2\) 时，\(\ln (x+1)+\sqrt{x+1}-1<\dfrac{9x}{x+6}\)．

解：

设 \(f(x)=\ln(x+1)+\sqrt{x+1}-1-\dfrac{9x}{x+6}\)，则只需证 \(f(x)_{\max}<0\)．

由均值不等式，有 \(g(x)=\ln(x+1)+\dfrac{x+1+1}{2}-1-\dfrac{9x}{x+6}\)，且 \(f(x)\le g(x)<0\)．

故原命题成立．

T4

已知 \(f(x)=a\mathrm{e}^x\ln x+\dfrac{b\mathrm{e}^{x-1}}{x}\)，曲线 \(y=f(x)\) 在点 \((1,f(1))\) 处的切线方程 \(y=\mathrm{e}(x-1)+2\)．求证：\(f(x)>1\)．

解：

代入切线方程可得 \(a=1,b=2\)．则 \(f(x)=\mathrm{e}^x\ln x+\dfrac{2\mathrm{e}^{x-1}}{x}\)，只需证 \(f(x)_{\min}>1\)．

将原式变形，只需证 \(x\ln x+\dfrac{2}{\mathrm{e}}>\dfrac{x}{\mathrm{e}^x}\)．设 \(g(x)=x\ln x+\dfrac{2}{\mathrm{e}},h(x)=\dfrac{x}{\mathrm{e}^x}\)．

求导，得 \(g'(x)=\ln x+1,h'(x)=\dfrac{1-x}{\mathrm{e}^x}\)，即 \(g(x)_{\min}=g\left(\dfrac{1}{\mathrm{e}}\right)=\dfrac{1}{\mathrm{e}},h(x)_{\max}=h(1)=\dfrac{1}{\mathrm{e}}\)．

因为 \(g(x)_{\min}=h(x)_{\max}\) 且最值在不同的 \(x\) 取到，故原命题成立．

零点问题

构（积）造（分）问题

T1

设函数 \(f(x)\) 满足 \(x^2f'(x)+2xf(x)=\dfrac{\mathrm{e}^x}{x}\)，\(f(2)=\dfrac{\mathrm{e}^2}{8}\)，则 \(x>0\) 时，\(f(x)\) 有无极大值和极小值？

解：

\(f(x)\) 既无极大值也无极小值．

注意到 \((x^2f(x))'=x^2f'(x)+2xf(x)\)，因此将原方程改写为 \((x^2f(x))'=\dfrac{\mathrm{e}^x}{x}\)．

令 \(g(x)=x^2f(x)\)，则 \(g'(x)=\dfrac{\mathrm{e}^x}{x}\) 且 \(f(x)=\dfrac{g(x)}{x^2}\)．

对 \(f(x)\) 求导：

\[f'(x)=\left(\frac{g(x)}{x^2}\right)'=\frac{xg'(x)-2g(x)}{x^3}=\frac{\mathrm{e}^x-2g(x)}{x^3}. \]

分母在 \(x>0\) 的时候恒大于 \(0\)，接下来分析分子．

设 \(h(x)=\mathrm{e}^x-2g(x)\)．

对 \(h(x)\) 求导：

\[h'(x)=(\mathrm{e}^x)'-2g'(x)=\frac{\mathrm{e}^x(x-2)}{x}. \]

故 \(h(x)_{\min}=h(2)=0\)．

故 \(h(x)\ge 0\) 恒成立，即 \(f'(x)\ge 0\) 恒成立．

故 \(f(x)\) 在 \((0,+\infty)\) 单调递增，无极大值和极小值．

T2

若实数 \(x,y\) 满足 \(4\ln x+2\ln y\ge x^2+4y-4\)，则
\( \text{A.}xy=\dfrac{\sqrt 2}{2}\qquad \text{B.}x+y=\sqrt 2\qquad \text{C.}2x+y=1+\sqrt 2\qquad \text{D.}x^3y=1\qquad \)

解：

移项并整理：

\[(4\ln x-x^2)+(2\ln y-4y)+4\ge 0. \]

设 \(f(x)=4\ln x-x^2\)，求导可得 \(f'(x)=\dfrac{4}{x}-2x\)，令 \(f'(x)=0\)，解得 \(x=\sqrt 2\)，分析可知 \(f(x)_{\max}=f(\sqrt 2)=2\ln 2-2\)．

设 \(g(y)=2\ln y-4y\)，求导可得 \(g'(y)=\dfrac{2}{y}-4\)，令 \(g'(y)=0\)，解得 \(y=\dfrac{1}{2}\)，分析可知 \(g(x)_{\max}=g\left(\dfrac{1}{2}\right)=-2\ln 2-2\)．

故 \((4\ln x-x^2)+(2\ln y-4y)+4\ge 0\) 左边最大为 \(0\)，而左边又必须满足大于等于 \(0\)，故不等式必须取等号，且必然有

\[x=\sqrt 2,y=\frac{1}{2}. \]

回代，可得 \(\text{A}\) 项正确．