zkw 线段树
拜谢 Tmbcan 大爷让我知道了这个优美的数据结构。我在拜读 Tmbcan 大爷的论文时和在平时写题的应用过程中也遇到了不少问题,所以本文更应当是对 Tmbcan 大爷的论文的补充。本文不追求面面俱到,但一定会记录最常用的 zkw 线段树技巧和注意事项。
约定:
- \(\log x\) 表示以 \(2\) 为底 \(x\) 的对数。
前置知识
递归式线段树,基础位运算。
效率比对
我们首先要知道 zkw 线段树是依靠递推实现的线段树,由于省去了递归造成的开销、大量结合位运算以及节点内存连续性好等优势使之效率大大高于递归式线段树,以下是数据的比对:
实现
zkw 线段树的优雅之处在于可以 \(O(1)\) 定位叶子节点。
首先要说明 zkw 线段树不同于递归线段树的特点:
- 递推实现;
- 自底向上更新节点信息;
- zkw 线段树的叶子节点那一层至少有 \(n+2\) 个节点。除了 \(n\) 个表示区间长度为 \(1\) 的节点外还有左右哨兵节点。
由于递归线段树的建树方式可能导致叶子节点不在同一层,难以自底向上地递推地维护信息,所以我们改变建树方式:令叶子节点在同一层,再层层递推向上。下图演示了一个 zkw 线段树的结构:
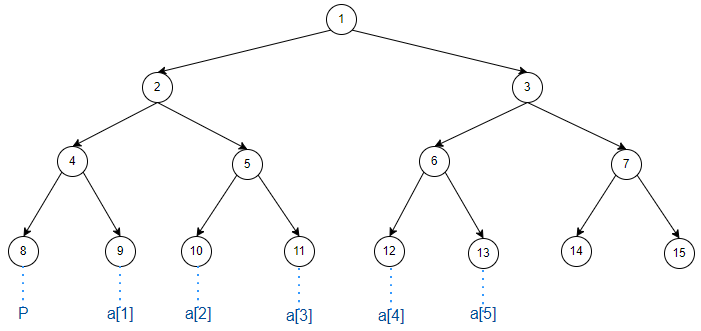
\(P\) 点即为左哨兵。根据图片我们发现一些性质:
- \(P\) 点的下标为 \(2^{\lceil\log (n+2)\rceil}\);
- 叶子节点那一层的节点数(包括空节点)为 \(2^{\lceil\log (n+2)\rceil}\);
- 与递归式线段树相同,一个下标为 \(x\) 的节点的左右儿子下标分别为 \(2x\) 和 \(2x+1\)。
我们可以通过 \(P\) 点的位置来辅助我们进行一系列操作。
根据 \(P\) 点的下标,我们可以得知数组最大访问到 \(2^{\lceil\log (n+2)\rceil}+n\) 处(右虚点不会作为下标被访问)。
函数 \(f(n)=2^{\lceil\log (n+2)\rceil}+n\) 在绝大多数情况下小于 \(3n\),但是在 \(n\) 接近 \(2\) 的整次幂时会略大于 \(3n\)。可以在这里详细观察函数间的关系。事实上,空间开 \(3n+10\) 即可。这优于递归线段树的 \(4\) 倍空间。
P=1;while(P<=n+1) P<<=1,++DEP;
容易看出,表示 \([i,i]\) 的叶子节点的下标为 \(P+i\),这就是 zkw 线段树 \(O(1)\) 访问任意叶子节点的方法。相应地,zkw 线段树在全局查询时具有一定劣势,详见下文。
以下均以 【模板】线段树 1 为例。
建树
既然可以确定叶子节点的位置,建树也就可以很自然地写出来:
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
for(int i=1;i<=n;i++) tree[P+i]=a[i];
for(int i=P-1;i;i--)
if(rs(i)<=P+n+1) tree[i]=tree[ls(i)]+tree[rs(i)];
注意:一定要判儿子是否合法,否则可能导致 RE。
懒标记下放
这个没有办法从下往上走,但是没关系。
线段树区间操作的本质是两条链上信息的合并/修改。所以我们每次操作仅需下放两条链上的懒标记即可。可以发现,每一层中的节点对应的区间大小相同。含有空节点的子树除外,但是由于这些节点不可能对答案做出贡献,故不影响正确性。如上图的 \(4\) 节点,虽然左儿子是空节点使得其对应的区间大小是 \(1\) 而非 \(2\),但是区间查询时它不可能被加入答案。这也导致很多情况下 \(1\) 号节点维护的可能不是正确的 \([1,n]\) 区间的信息。此时必须调用 query 函数进行全局查询,无法做到 \(O(1)\) 全局查询。除非你能确定可以排除虚点的影响。
区间操作
还是刚刚的线段树,操作区间 \([2,4]\):
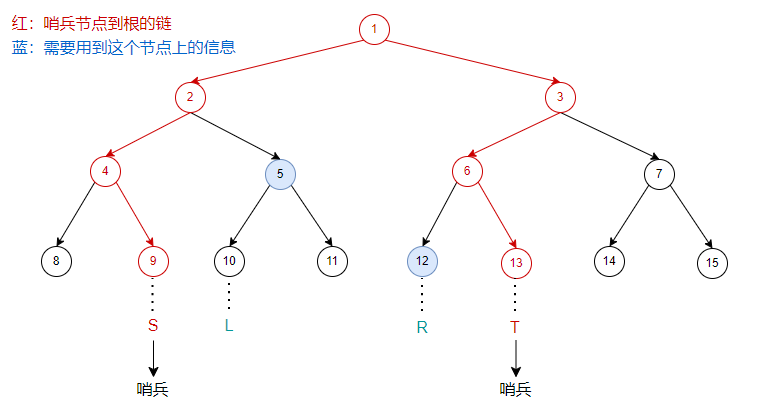
对于 zkw 线段树,需要先把闭区间操作转为开区间操作。
- 对于左链,当其上的节点作为左儿子时,其兄弟节点需要累加贡献;
- 对于右链,当其上的节点作为右儿子时,其兄弟节点需要累加贡献。
当两条链汇合时,也就是向上递推过程中两链上的点互为兄弟节点时,停止操作。如果是修改操作需要将信息更新继续更新至根节点。
inline void push_down(int u,int siz){
if(!tag[u]) return;
siz>>=1;
tag[ls(u)]+=tag[u],tag[rs(u)]+=tag[u];
tree[ls(u)]+=tag[u]*siz,tree[rs(u)]+=tag[u]*siz;
tag[u]=0;
}
inline void modify(int l,int r,ll k){
l+=P-1,r+=P+1;
int siz=1;
for(int i=DEP;i;i--)
push_down(l>>i,1<<i),push_down(r>>i,1<<i);
while(l^1^r){
if(~l&1) tree[l^1]+=k*siz,tag[l^1]+=k;
if(r&1) tree[r^1]+=k*siz,tag[r^1]+=k;
l>>=1,r>>=1,siz<<=1;
tree[l]=tree[ls(l)]+tree[rs(l)];
tree[r]=tree[ls(r)]+tree[rs(r)];
}
for(l>>=1;l;l>>=1)
tree[l]=tree[ls(l)]+tree[rs(l)];
}
inline ll query(int l,int r){
l+=P-1,r+=P+1;
ll res=0;
for(int i=DEP;i;i--)
push_down(l>>i,1<<i),push_down(r>>i,1<<i);
while(l^1^r){
if(~l&1) res+=tree[l^1];
if(r&1) res+=tree[r^1];
l>>=1,r>>=1;
}
return res;
}
你可以标记永久化以实现更强的常数优化。这里不详细展开。
单点操作
zkw 线段树的单点操作惊人的简洁:
inline void modify(int x,int k){
x+=P,tree[x]+=k;
for(x>>=1;x;x>>=1) tree[x]=tree[ls(x)]+tree[rs(x)];
}
进阶操作
无交换律信息
比如线段树维护矩阵、线段树维护哈希和线段树维护跨区间信息等。
这样的信息无交换律,query 时仅用 \(1\) 个量 \(res\) 无法正确合并信息,此时需要左右两条链各使用一个 \(res\),最后再合并。
这里以单点修改、区间最大子段和为例:
struct Node{
int maxl,maxr,maxn,sum;
inline friend Node operator+(const Node &x,const Node &y){
if(x.maxl==-inf) return y;
if(y.maxl==-inf) return x;
Node res;
res.sum=x.sum+y.sum;
res.maxl=max(x.maxl,x.sum+y.maxl);
res.maxr=max(y.maxr,y.sum+x.maxr);
res.maxn=max({x.maxn,y.maxn,x.maxr+y.maxl});
return res;
}
}tree[N*3];
inline void build(){
for(int i=1;i<=P;i++) tree[i]={-inf};
for(int i=1;i<=n;i++) tree[P+i]={a[i],a[i],a[i],a[i]};
tree[P+n+1]={-inf};
for(int i=P-1;i;i--)
if(rs(i)<=P+n+1) tree[i]=tree[ls(i)]+tree[rs(i)];
}
inline void modify(int x,int k){
x+=P;tree[x]={k,k,k,k};
for(x>>=1;x;x>>=1) tree[x]=tree[ls(x)]+tree[rs(x)];
}
inline int query(int l,int r){
l+=P-1,r+=P+1;
Node resl={-inf},resr={-inf};
while(l^1^r){
if(~l&1) resl=resl+tree[l^1];
if(r&1) resr=tree[r^1]+resr;
l>>=1,r>>=1;
}
return (resl+resr).maxn;
}
线段树上二分
全局第 \(k\) 小:
inline int kth(int k){
int x=1;
for(int i=1;i<=DEP;i++){
if(tree[x<<1]>=k) x=x<<1;
else k-=tree[x<<1],x=x<<1|1;
}
return x-P;
}
动态开点
没有必要写 zkw 线段树了,你都动态开点了不差这点常数。
总结
zkw 线段树的特性:
- 相对于递归线段树有更小的时空常数;
- \(O(\log n)\) 一般区间操作;
- \(O(1)\) 访问任意叶子节点;
- 一些情况下必须 \(O(\log n)\) 全局查。想做到 \(O(1)\) 可能需要一些特殊处理排除虚点干扰。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号