二叉搜索树 & 平衡树
二叉搜索树
性质
- 显然二叉搜索树是一棵二叉树。
- 空树是二叉搜索树。
- 二叉搜索树的左右子树也是二叉搜索树。
- 二叉搜索树的左子树上任意一个节点的权值均小于根节点的权值,右子树上任意一个节点的权值均大于根节点的权值。
二叉搜索树上的基本操作时间复杂度大多为 \(O(h)\),\(h\) 为二叉搜索树的高度。若二叉搜索树有 \(n\) 个节点,则最优时间复杂度为 \(O(\log n)\)(完全二叉树),最坏时间复杂度为 \(O(n)\)(退化成链)。
显然,二叉搜索树很容易被卡,我们需要上优化。
平衡树
二叉搜索树复杂度之所以不稳定,在于其操作大多与树的高度有关。平衡树通过维护平衡性维持树的高度,降低时间复杂度。
Splay
一种二叉平衡树,通过 Splay(伸展)操作,在 \(O(\log n)\) 时间内实现插入、查询和删除操作。注意,\(O(\log n)\) 为 Splay 的均摊时间复杂度而非单次时间复杂度。常数在平衡树中属于较大的。
平衡的调整
我们使用左旋(zag)和右旋(zig)操作维护平衡性。注意,维护平衡性时不能改变中序遍历序列。
先说右旋操作,我们有一棵二叉搜索树
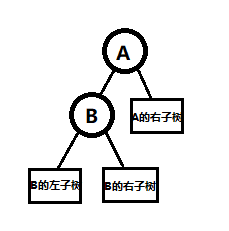
我们将 \(B\) 向右上旋转,成为新的根节点,\(A\) 向右下旋转成为 \(B\) 的右子树的根节点,\(B\) 的右子树变为 \(A\) 的左子树。
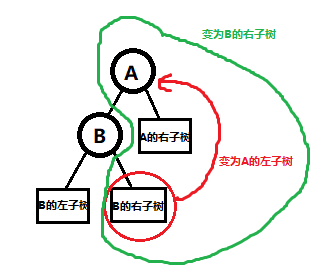
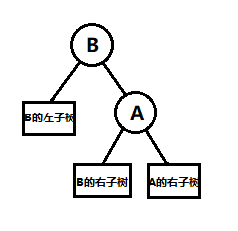
左旋与右旋互为镜像。将第三张图中的树左旋可得到第一张图中的树。
变量声明
int son[N][2];//son[i][0/1]表示节点i的左/右儿子编号
int fa[N];//父节点
int tot;//已使用节点个数
int val[N];//val[i]为节点i的权值
int cnt[N];//cnt[i]为节点i所对权值出现的次数
int siz[N];//子树的大小
辅助操作
bool dir(int x){//判断节点x是父节点的左儿子还是右儿子
return x==son[fa[x]][1];
}
void push_up(int x){//更新节点x的信息
siz[x]=cnt[x]+siz[son[x][0]]+siz[son[x][1]];
}
旋转操作
设需要上移节点 \(x\),进行右旋操作。
void rotate(int x){
/*右旋
z z
/ /
y x
/ \ -> / \
x yr xl y
/ \ / \
xl xr xr yr
左旋
z z
\ \
y x
/ \ -> / \
yl x y xr
/ \ / \
xl xr yl xl
*/
int y=fa[x],z=fa[y];
bool r=dir(x);
son[y][r]=son[x][!r];//x的子节点转移到y
if(son[x][!r])
fa[son[x][!r]]=y;
fa[x]=z;//x变为z的子节点
if(z)
son[z][dir(y)]=x;
son[x][!r]=y;//y变为x的子节点
fa[y]=x;
push_up(y);
push_up(x);
return;
}
伸展操作
Splay 树要求访问每一个节点 \(x\) 后强制其旋转到根节点。该操作就是伸展操作。通过一系列伸展步骤将 \(x\) 逐步移到根节点。记 \(x\) 的父节点为 \(p\),伸展步骤有三种:
- zig/zag:当 \(p\) 为根节点时,直接将 \(x\) 左旋或右旋。在 \(x\) 在伸展操作刚开始时深度为奇数时作为伸展操作的最后一步。
- zig-zig/zag-zag(一字型):当 \(p\) 不是根节点且 \(x\) 和 \(p\) 都是左侧子节点或都是右侧子节点时进行。首先将 \(p\) 旋转,然后将 \(x\) 旋转。
- zig-zag/zag-zig(之字型):当 \(p\) 不是根节点且 \(x\) 和 \(p\) 一个为左侧子节点一个为右侧子节点时进行。将 \(x\) 先左旋再右旋或先右旋再左旋。
void splay(int &z,int x){//z为根节点
int temp=fa[z];
while(fa[x]!=temp){
int y=fa[x];
if(fa[y]!=temp){
if(dir(x)==dir(y))
rotate(y);//一字型
else
rotate(x);//之字型
}
rotate(x);
}
z=x;
return;
}
平衡树操作
按照值查找
查找值 \(v\),并将 \(v\) 所对节点上移至根部。
若不存在值为 \(v\) 的节点,则要将最后一个访问到的节点上移至根部。此时的根为所有大于 \(v\) 的值中最小的或所有小于 \(v\) 的值中最大的。
void find(int &z,int v){//该函数调用后的根节点即为返回值
int x=z,y=fa[x];
while(x&&val[x]!=v){
y=x;
if(v<val[x])
x=son[x][0];
else
x=son[x][1];
}
splay(z,x?x:y);
return;
}
按照排名访问
即查找树中第 \(k\) 小的元素。利用记载的子树大小进行查找。
void loc(int &z,int k){
int x=z;
while(1){
if(siz[son[x][0]]>=k)
x=son[x][0];
else if(siz[son[x][0]]+cnt[x]>=k)
break;
else{
k-=siz[son[x][0]]+cnt[x];
x=son[x][1];
}
}
splay(z,x);
return;
}
合并
合并两棵 Splay 树,设根节点分别为 \(x\) 和 \(y\),则需要 \(x\) 树中的最大值小于 \(y\) 中的最小值。
int merge(int x,int y){//x树中的最大值小于y树中的最小值,返回合并后的根节点
if(!x||!y)
return x|y;//存在空树,直接返回
loc(y,1);//将y树最小值移至根节点
son[y][0]=x;//此时y左节点必然为空
fa[x]=y;//x成为y的左子树
push_up(y);
return y;
}
分裂
根据某值 \(v\),将 Splay 树分裂为值小于等于 \(v\) 和大于 \(v\) 两部分。
void split(int x,int v,int &a,int &b){//通过引用返回分裂后的根节点a和b
//x为当前根节点,按照权值v分裂为小于等于v和大于v两部分
if(!x){
a=b=0;
return;//树为空
}
find(x,v);//将权值为v的节点旋转到根节点
if(val[x]<=v){
a=x;
b=son[x][1];
son[x][1]=0;
fa[b]=0;
push_up(a);
}
else{
b=x;
a=son[x][0];
son[x][0]=0;
fa[a]=0;
push_up(b);
}
return;
}
插入
void insert(int &z,int v){
int x=z,y=0;
while(x&&val[x]!=v){
y=x;
if(v<val[x])
x=son[x][0];
else
x=son[x][1];
}
if(x)
cnt[x]++,siz[x]++;
else{
x=++tot;
val[x]=v;
cnt[x]=siz[x]=1;
fa[x]=y;
if(y){
if(v<val[y])
son[y][0]=x;
else
son[y][1]=x;
}
}
splay(z,x);//插入过后不要忘记转到根节点
return;
}
删除
bool erase(int &z,int v){
find(z,v);
if(!z||val[z]!=v)
return 0;//删除失败
cnt[z]--,siz[z]--;
if(!cnt[z]){//该节点对应的值被删完了
int x=son[z][0],y=son[z][1];
fa[x]=fa[y]=0;
z=merge(x,y);
}
return 1;//删除成功
}
查询排名
查询值 \(v\) 的排名。
int find_rank(int &z,int v){
find(z,v);
int res=siz[son[z][0]]+1;
if(val[z]<v)
res+=cnt[z];
return res;
}
查询前驱
即查询小于 \(v\) 的最大的数。
int find_pre(int &z,int v){
find(z,v);
if(z&&val[z]<v)
return val[z];
int x=son[z][0];//在左子树中查找最大值
if(!x)
return -inf;
while(son[x][1])
x=son[x][1];
splay(z,x);
return val[z];
}
查询后继
即查询大于 \(v\) 的最小的数。
int find_nxt(int &z,int v){
find(z,v);
if(z&&val[z]>v)
return val[z];
int x=son[z][1];//在右子树中查找最小值
if(!x)
return inf;
while(son[x][0])
x=son[x][0];
splay(z,x);
return val[z];
}
序列操作
区间翻转
我们需要在树中加入值为 \(-\inf\) 和 \(\inf\) 两个哨兵节点,防止翻转区间包含第 \(1\) 个节点或最后一个节点时出事。与线段树类似,我们使用懒标记记录翻转情况。
void reverse(int l,int r){
loc(root,l);//将l转至根节点
loc(son[root][1],r-l+2);//将r转至根节点的右儿子,由于根已改变,所以第二个参数传的是r-l+2
int x=son[son[root][1]][0];//根节点右儿子的左儿子,则x为区间[l,r]的根节点
update_tag(x);
push_down(x);
splay(root,x);
return;
}
辅助操作:
void update_tag(int x){
swap(son[x][0],son[x][1]);
tag[x]^=1;
return;
}
void push_down(int x){
if(tag[x]){
if(son[x][0])
update_tag(son[x][0]);
if(son[x][1])
update_tag(son[x][1]);
tag[x]=0;
}
return;
}
同时,\(\operatorname{loc}\) 函数查找时要更新懒标记
void loc(int &z,int k){
int x=z;
push_down(x);
while(1){
if(siz[son[x][0]]>=k)
x=son[x][0];
else if(siz[son[x][0]]+1>=k)
break;
else{
k-=siz[son[x][0]]+1;
x=son[x][1];
}
push_down(x);
}
splay(z,x);
return;
}
无注释版代码
模板题 1 主体部分
bool dir(int x){
return x==son[fa[x]][1];
}
void push_up(int x){
siz[x]=cnt[x]+siz[son[x][0]]+siz[son[x][1]];
}
void rotate(int x){
int y=fa[x],z=fa[y];
bool r=dir(x);
son[y][r]=son[x][!r];
if(son[x][!r])
fa[son[x][!r]]=y;
fa[x]=z;
if(z)
son[z][dir(y)]=x;
son[x][!r]=y;
fa[y]=x;
push_up(y);
push_up(x);
return;
}
void splay(int &z,int x){
int temp=fa[z];
while(fa[x]!=temp){
int y=fa[x];
if(fa[y]!=temp){
if(dir(x)==dir(y))
rotate(y);
else
rotate(x);
}
rotate(x);
}
z=x;
return;
}
void find(int &z,int v){
int x=z,y=fa[x];
while(x&&val[x]!=v){
y=x;
if(v<val[x])
x=son[x][0];
else
x=son[x][1];
}
splay(z,x?x:y);
return;
}
void loc(int &z,int k){
int x=z;
while(1){
if(siz[son[x][0]]>=k)
x=son[x][0];
else if(siz[son[x][0]]+cnt[x]>=k)
break;
else{
k-=siz[son[x][0]]+cnt[x];
x=son[x][1];
}
}
splay(z,x);
return;
}
int merge(int x,int y){
if(!x||!y)
return x|y;
loc(y,1);
son[y][0]=x;
fa[x]=y;
push_up(y);
return y;
}
void insert(int &z,int v){
int x=z,y=0;
while(x&&val[x]!=v){
y=x;
if(v<val[x])
x=son[x][0];
else
x=son[x][1];
}
if(x)
cnt[x]++,siz[x]++;
else{
x=++tot;
val[x]=v;
cnt[x]=siz[x]=1;
fa[x]=y;
if(y){
if(v<val[y])
son[y][0]=x;
else
son[y][1]=x;
}
}
splay(z,x);
return;
}
bool erase(int &z,int v){
find(z,v);
if(!z||val[z]!=v)
return 0;
cnt[z]--,siz[z]--;
if(!cnt[z]){
int x=son[z][0],y=son[z][1];
fa[x]=fa[y]=0;
z=merge(x,y);
}
return 1;
}
int find_rank(int &z,int v){
find(z,v);
int res=siz[son[z][0]]+1;
if(val[z]<v)
res+=cnt[z];
return res;
}
int find_pre(int &z,int v){
find(z,v);
if(z&&val[z]<v)
return val[z];
int x=son[z][0];
if(!x)
return -1;
while(son[x][1])
x=son[x][1];
splay(z,x);
return val[z];
}
int find_nxt(int &z,int v){
find(z,v);
if(z&&val[z]>v)
return val[z];
int x=son[z][1];
if(!x)
return -1;
while(son[x][0])
x=son[x][0];
splay(z,x);
return val[z];
}
模板题 2 主体部分
#include<algorithm>
using namespace std;
const int N=1e5+10;
int son[N][2],fa[N],tot,val[N],siz[N],root;
bool tag[N];
bool dir(int x){
return x==son[fa[x]][1];
}
void push_up(int x){
siz[x]=1+siz[son[x][0]]+siz[son[x][1]];
}
void update_tag(int x){
swap(son[x][0],son[x][1]);
tag[x]^=1;
return;
}
void push_down(int x){
if(tag[x]){
if(son[x][0])
update_tag(son[x][0]);
if(son[x][1])
update_tag(son[x][1]);
tag[x]=0;
}
return;
}
void rotate(int x){
int y=fa[x],z=fa[y];
bool r=dir(x);
son[y][r]=son[x][!r];
if(son[x][!r])
fa[son[x][!r]]=y;
fa[x]=z;
if(z)
son[z][dir(y)]=x;
son[x][!r]=y;
fa[y]=x;
push_up(y);
push_up(x);
return;
}
void splay(int &z,int x){
int temp=fa[z];
while(fa[x]!=temp){
int y=fa[x];
if(fa[y]!=temp){
if(dir(x)==dir(y))
rotate(y);
else
rotate(x);
}
rotate(x);
}
z=x;
return;
}
void loc(int &z,int k){
int x=z;
push_down(x);
while(1){
if(siz[son[x][0]]>=k)
x=son[x][0];
else if(siz[son[x][0]]+1>=k)
break;
else{
k-=siz[son[x][0]]+1;
x=son[x][1];
}
push_down(x);
}
splay(z,x);
return;
}
void reverse(int l,int r){
loc(root,l);
loc(son[root][1],r-l+2);
int x=son[son[root][1]][0];
update_tag(x);
push_down(x);
splay(root,x);
return;
}
void build(int n){
for(int i=0;i<=n+1;i++){
son[++tot][0]=root;
if(root)
fa[root]=tot;
root=tot;
val[tot]=i;
siz[tot]=1;
push_up(root);
}
splay(root,1);
return;
}
Treap
Treap 将二叉搜索树与堆结合起来,通过维护堆的性质维护平衡。所以每个节点需要额外维护一个随机的值,用这个随机的值来维护堆的性质。这里介绍旋转 Treap,即通过旋转维护平衡性。
Code
#include<algorithm>
using namespace std;
const int N=1e5+10;
int son[N][2],val[N],rnd[N],siz[N],cnt[N],tot,root;
void push_up(int x){
siz[x]=cnt[x]+siz[son[x][0]]+siz[son[x][1]];
}
void rotate(int &x,bool dir){
int temp=son[x][!dir];
son[x][!dir]=son[temp][dir];
son[temp][dir]=x;
x=temp;
push_up(son[x][dir]);
push_up(x);
}
void insert(int &x,int v){
if(!x){
x=++tot;
siz[x]=cnt[x]=1;
val[x]=v;
rnd[x]=rand();
return;
}
if(val[x]==v)
cnt[x]++;
else{
bool dir=(v>val[x]);
insert(son[x][dir],v);
if(rnd[x]<rnd[son[x][dir]])
rotate(x,!dir);
}
push_up(x);
}
void erase(int &x,int v){
if(!x)
return;
if(v<val[x])
erase(son[x][0],v);
else if(v>val[x])
erase(son[x][1],v);
else{
if(cnt[x]>1){
cnt[x]--;
push_up(x);
return;
}
if(son[x][0]||son[x][1]){
if(!son[x][1]||rnd[son[x][0]]>rnd[son[x][1]])
rotate(x,1),erase(son[x][1],v);
else
rotate(x,0),erase(son[x][0],v);
push_up(x);
}
else
x=0;
}
push_up(x);
}
int find_rank(int x,int v){
if(!x)
return 1;
if(v==val[x])
return siz[son[x][0]]+1;
if(v<val[x])
return find_rank(son[x][0],v);
return siz[son[x][0]]+cnt[x]+find_rank(son[x][1],v);
}
int find(int x,int k){
if(!x)
return 0;
if(siz[son[x][0]]>=k)
return find(son[x][0],k);
if(siz[son[x][0]]+cnt[x]>=k)
return val[x];
return find(son[x][1],k-siz[son[x][0]]-cnt[x]);
}
int find_pre(int v){
int x=root,pre;
while(x){
if(v>val[x])
pre=val[x],x=son[x][1];
else
x=son[x][0];
}
return pre;
}
int find_nxt(int v){
int x=root,nxt;
while(x){
if(v<val[x])
nxt=val[x],x=son[x][0];
else
x=son[x][1];
}
return nxt;
}
无旋 Treap
通过分裂和合并来维护平衡性。因其无旋,所以可以做可持久化数据结构,并且是平衡树中比较好写的一种。缺点是常数较大。
模板题 1 AC 代码
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=1e5+10;
struct FHQ_Treap{
int ls,rs;
int val,rnd,siz;
}t[N];
int root,tot;
void push_up(int u){
t[u].siz=t[t[u].ls].siz+t[t[u].rs].siz+1;
}
int build(int val){
t[++tot].rnd=rand()<<15|rand();
t[tot].siz=1;
t[tot].val=val;
return tot;
}
void split(int p,int val,int &lrt,int &rrt){
if(!p){
lrt=rrt=0;
return;
}
if(t[p].val<=val){
lrt=p;
split(t[p].rs,val,t[p].rs,rrt);
}
else{
rrt=p;
split(t[p].ls,val,lrt,t[p].ls);
}
push_up(p);
return;
}
int merge(int l,int r){
if(!l||!r)
return l|r;
if(t[l].rnd>t[r].rnd){
t[l].rs=merge(t[l].rs,r);
push_up(l);
return l;
}
else{
t[r].ls=merge(l,t[r].ls);
push_up(r);
return r;
}
}
void insert(int val){
int x,y;
split(root,val,x,y);
root=merge(merge(x,build(val)),y);
return;
}
void erase(int val){
int x,y,temp;
split(root,val,x,y);
split(x,val-1,x,temp);
temp=merge(t[temp].ls,t[temp].rs);
root=merge(merge(x,temp),y);
return;
}
int find_rank(int val){
int x,y;
split(root,val-1,x,y);
int res=t[x].siz+1;
root=merge(x,y);
return res;
}
int find_kth(int k){
int p=root;
while(1){
if(t[t[p].ls].siz+1==k)
break;
else if(t[t[p].ls].siz+1>k)
p=t[p].ls;
else
k-=t[t[p].ls].siz+1,p=t[p].rs;
}
return t[p].val;
}
int pre(int val){
int x,y;
split(root,val-1,x,y);
int p=x;
while(t[p].rs)
p=t[p].rs;
root=merge(x,y);
return t[p].val;
}
int nxt(int val){
int x,y;
split(root,val,x,y);
int p=y;
while(t[p].ls)
p=t[p].ls;
root=merge(x,y);
return t[p].val;
}
int n,opt,x;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d%d",&opt,&x);
switch(opt){
case 1:
insert(x);
break;
case 2:
erase(x);
break;
case 3:
printf("%d\n",find_rank(x));
break;
case 4:
printf("%d\n",find_kth(x));
break;
case 5:
printf("%d\n",pre(x));
break;
default:
printf("%d\n",nxt(x));
break;
}
}
return 0;
}
特别鸣谢,为我解答了很多问题,以及帮我进行代码的修正。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号