论文阅读 Attention Is All You Need

注意力机制的基本思想和实现原理
一文读懂「Attention is All You Need」| 附代码实现
细讲 | Attention Is All You Need
《Attention Is All You Need 》阅读笔记

本来想着放这些参考资料好了，还是觉得自己对着原来的论文捋了一遍，初略看一下好一些，基本机翻

Attention Is All You Need

• 摘要
• 1 引言
• 2 背景
• 3 模型架构
• • 3.1 编码器和解码器堆栈
  • 3.2 注意力
  • • 3.2.1 点积的按比例缩放
    • 3.2.2 多头注意力
    • 3.2.3 注意力在我们模型中的应用
  • 3.3 位置前馈网络
  • 3.4 嵌入和Softmax
  • 3.5 位置编码
• 为什么自注意力

摘要

优势序列转导模型基于复杂的递归或卷积神经网络，包括编码器和解码器。表现最佳的模型还通过注意力机制连接编码器和解码器。我们提出了一种新的简单网络架构，即Transformer，它完全基于注意力机制，完全消除了重复和卷积。在两个机器翻译任务上进行的实验表明，这些模型在质量上具有优势，同时具有更高的可并行性，并且所需的训练时间明显更少。我们的模型在WMT 2014英语到德语的翻译任务中达到了28.4 BLEU，比包括乐团在内的现有最佳结果提高了2 BLEU。在WMT 2014英语到法语翻译任务中，我们的模型在八个GPU上进行了3.5天的训练后，建立了新的单模型最新BLEU分数41.8。文献中的模型。我们展示了Transformer通过将其成功应用于具有大量训练数据和有限训练数据的英语选区解析，将其很好地概括了其他任务。

1 引言

递归神经网络，特别是长短时记忆和门控循环神经网络，在语言建模和机器翻译中都被很好的检验过了。此后，人们一直在努力的扩大循环语言模型和编码器-解码器体系结构的界限。

循环模型通常沿输入和输出序列的符号位置考虑计算。将位置与计算时间中的步骤对齐，它们会根据先前的隐藏状态h_t-1和位置t的输入生成一系列隐藏状态h_t。这种固有的顺序性质阻止了训练示例内的并行化，这在较长的序列长度上变得至关重要，因为内存限制限制了示例之间的批处理，最近的工作通过分解技巧[21]和条件计算[32]在计算效率上取得了显着提高，同时在后者的情况下还提高了模型性能。但是，顺序计算的基本约束仍然存在。

注意机制已成为各种任务中引人注目的序列建模和转导模型不可或缺的一部分，从而允许对依赖项进行建模，而无需考虑它们在输入或输出序列中的距离[2，19]。但是，在少数情况下[27]，在所有情况下，此类注意力机制都与循环网络结合使用。

在这项工作中，我们提出了一种Transformer，它是一种避免重复发生的模型体系结构，而是完全依赖于注意力机制来绘制输入和输出之间的全局依存关系。在八个P100 GPU上进行了长达12个小时的培训之后，该Transformer可以实现更多的并行化，并可以在翻译质量方面达到最新的水平。

2 背景

减少顺序计算的目标也构成了扩展神经GPU [16]，ByteNet [18]和ConvS2S [9]的基础，它们全部使用卷积神经网络作为基本构件，并行计算所有输入和输出的隐藏表示。输出位置。在这些模型中，关联来自两个任意输入或输出位置的信号所需的操作数在位置之间的距离中增加，对于ConvS2S线性增长，而对于ByteNet则对数增长。这使得学习远距离之间的依存关系变得更加困难[12]。在Transformer中，这可以减少到恒定的操作次数，尽管会因平均注意力加权位置而导致有效分辨率降低的代价，这是我们用3.2中所述的多头注意力抵消的效果。

自我注意，有时也称为内部注意，是一种与单个序列的不同位置相关的注意力机制，目的是计算序列的表示形式。自我注意已成功用于各种任务中，包括阅读理解，抽象性摘要，文本蕴涵和学习与任务无关的句子表示[4，27，28，22]

端到端存储网络基于递归注意机制，而不是序列对齐的递归，并且已被证明在简单语言问答和语言建模任务中表现良好[34]。

据我们所知，Transformer是第一个完全依靠自我注意力来计算其输入和输出表示的转导模型，而无需使用序列对齐的RNN或卷积。在以下各节中，我们将描述变形金刚，激发自我注意并讨论其相对于模型[17、18]和[9]的优势

3 模型架构

大多数竞争性神经序列转导模型都具有编码器-解码器结构[5，2，35]。在此，编码器将符号表示形式（x1，…，xn）的输入序列映射到连续表示形式z =（z1，…，zn）的序列。给定z，解码器然后一次生成一个元素的符号的输出序列（y1，…，ym）。模型的每一步都是自回归的[10]，在生成下一个时，会将先前生成的符号用作附加输入。

变压器遵循这种总体架构，对编码器和解码器使用堆叠式自注意力和逐点，全连接层，分别如图1的左半部分和右半部分所示。

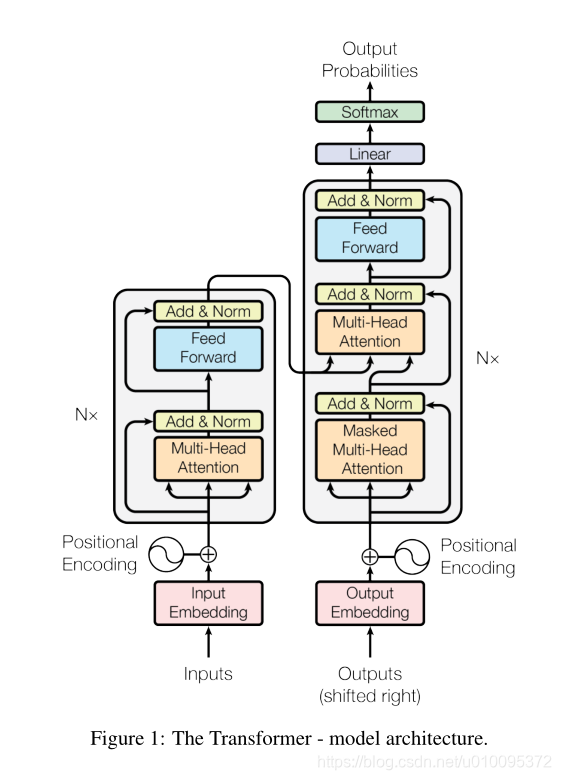
3.1 编码器和解码器堆栈

编码器： 编码器由N = 6个相同层的堆栈组成。每层都有两个子层。第一个是多头自我关注机制，第二个是简单的位置完全连接的前馈网络。我们在两个子层的每一层周围采用了残余连接[11]，然后进行层归一化[1]。也就是说，每个子层的输出是LayerNorm（x + Sublayer（x）），其中Sublayer（x）是由子层本身实现的功能。为了促进这些残留连接，模型中的所有子层以及嵌入层均产生尺寸为d_model = 512的输出。

解码器： 解码器还由N = 6个相同层的堆栈组成。除了每个编码器层中的两个子层之外，解码器还插入第三子层，该第三子层对编码器堆栈的输出执行多头关注。与编码器类似，我们在每个子层周围采用残余连接，然后进行层归一化。我们还修改了解码器堆栈中的自我注意子层，以防止位置关注后续位置。这种掩盖，加上输出嵌入被一个位置偏移的事实，确保了对位置i的预测只能依赖于小于i位置的已知输出。

3.2 注意力

注意功能可以描述为将查询和一组键值对映射到输出，其中查询，键，值和输出都是向量。将输出计算为值的加权总和，其中分配给每个值的权重是通过查询与相应键的兼容性函数来计算的

3.2.1 点积的按比例缩放

我们将我们的特别关注称为“点状产品关注度”（图2）。输入由维度为dk的查询和键以及维度为dv的值组成。我们用所有键计算查询的点积，将每个键除以√dk，然后应用softmax函数获得值的权重。

实际上，我们在一组查询上同时计算注意力函数，将它们打包到一个矩阵Q中。键和值也打包在一个矩阵K和V中。我们将输出矩阵计算为：

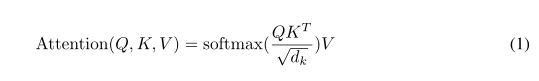
两种最常用的注意力功能是加性注意力[2]和点积（乘法）注意力。点积注意与我们的算法相同，只是比例因子为1√d_k。加性注意事项使用具有单个隐藏层的前馈网络来计算兼容性函数。尽管两者在理论上的复杂度相似，但是在实践中点积的关注要快得多，并且空间效率更高，因为可以使用高度优化的矩阵乘法代码来实现。

对于较小的d_k而言，这两种机制的表现类似，而加性注意的效果优于点积的注意，而无需针对较大的d_k进行缩放[3]。我们怀疑，对于较大的dk值，点积的幅度会增大，从而将softmax函数推入梯度极小的区域4。为了抵消这种影响，我们将点积缩放1√d_k

3.2.2 多头注意力

与使用d_model维的键，值和查询执行单个注意功能相比，我们发现将查询，键和值分别线性地投影h时间（分别具有不同的，学习的线性投影到d_k，d_k和d_v 维）是有益的。然后，在查询，键和值的这些预计的每个版本上，我们并行执行关注功能，从而产生dv维输出值。将它们连接起来并再次投影，得到最终值，如图2所示。

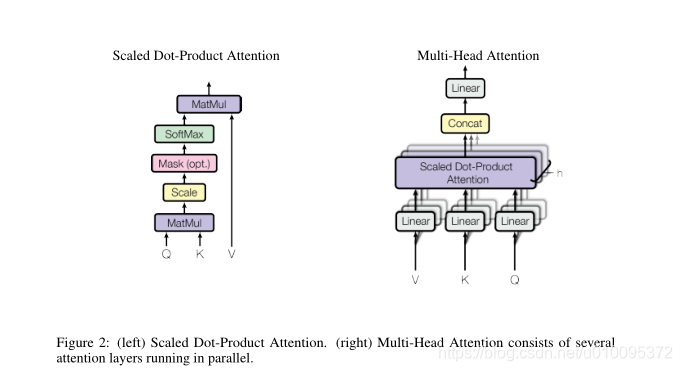
多头注意力使模型可以共同关注来自不同位置的不同表示子空间的信息。对于一个注意力集中的头部，平均抑制了这一点。

3.2.3 注意力在我们模型中的应用

Transformer 以三种不同方式使用多头注意力：

• 在“编码器-解码器注意”层中，查询来自先前的解码器层，而存储键和值来自编码器的输出。这允许解码器中的每个位置都参与输入序列中的所有位置。这模仿了序列到序列模型（例如[38、2、9]）中的典型编码器-解码器注意机制。
• 编码器包含自我注意层。在自我关注层中，所有键，值和查询都来自同一位置，在这种情况下，是编码器中上一层的输出。编码器中的每个位置都可以覆盖编码器上一层中的所有位置。
• 类似地，解码器中的自我关注层允许解码器中的每个位置都参与解码器中的所有位置，直到该位置为止。我们需要防止解码器中向左流动信息，以保留自回归属性。通过屏蔽（设置为-∞）softmax输入中与非法连接相对应的所有值，我们在缩放点积注意的内部实现了这一点。参见图2。

3.3 位置前馈网络

除了关注子层之外，我们的编码器和解码器中的每个层还包含一个完全连接的前馈网络，该网络被分别并相同地应用于每个位置。这由两个线性变换组成，两个线性变换之间具有ReLU激活。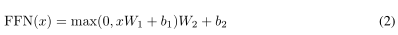
虽然线性变换在不同位置上相同，但是它们使用不同的参数。描述它的另一种方法是将两个卷积核尺寸为1。输入和输出的维数为d_model = 512，内层的维数为d_ff = 2048。

3.4 嵌入和Softmax

与其他序列转导模型相似，我们使用学习的嵌入将输入标记和输出标记转换为维d_model的向量。我们还使用通常学习的线性变换和softmax函数将解码器输出转换为预测的下一个令牌概率。在我们的模型中，我们在两个嵌入层和pre-softmax线性变换之间共享相同的权重矩阵，类似于[30]。在嵌入层中，我们将这些权重乘以√dmodel。

3.5 位置编码

由于我们的模型不包含递归和卷积，因此为了使模型能够使用序列的顺序，我们必须注入一些有关序列的相对或绝对位置的信息。为此，我们在编码器和解码器堆栈底部的输入嵌入中添加“位置编码”。位置编码的维数dmodel与嵌入的维数相同，因此可以将两者相加。位置编码有很多选择，可以学习和固定[9]。在这项工作中，我们使用不同频率的正弦和余弦函数：

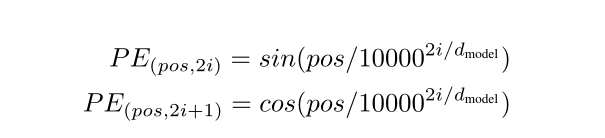
其中pos是位置，i是尺寸。即，位置编码的每个维度对应于正弦曲线。波长形成从2π到10000·2π的几何级数。我们选择此函数是因为我们假设它会允许模型轻松学习相对位置，因为对于任何固定的偏移量k，PE~pos + k_{可以表示为PE}pos~的线性函数。

我们还尝试使用学习的位置嵌入[9]进行实验，发现这两个版本产生的结果几乎相同（请参见表3（E）行）。我们选择正弦曲线版本是因为它可以使模型外推到比训练过程中遇到的序列更长的序列长度。

为什么自注意力

在本节中，我们将自我注意层的各个方面与通常用于将一个可变长度的符号表示序列（x₁，…，x_n）映射到另一个长度相等的序列（z₁，…z_n）的循环层和卷积层进行比较。其中x_i，z_i∈R^d，例如典型序列转导编码器或解码器中的隐藏层。为了激发我们的自我注意力，我们考虑了三个必需条件。
一种是每层的总计算复杂度。另一个是可以并行化的计算量，以所需的最少顺序操作数衡量。
第三个是网络中远程依赖关系之间的路径长度。