学习极大似然的若干笔记

文章目录

• 贝叶斯公式
• 似然函数
• 最大似然估计(MLE)
• 最大后验概率估计(MAP)
• 贝叶斯估计
• Reference

贝叶斯公式

贝叶斯可以这么理解
因为P(A|B)P(B)=P(A∩B)=P(B|A)P(A)，所以可以推出P(A|B)=P(B|A)*P(A)/P(B)
更一般可以这样理解
P(规律|现象) = P(现象|规律)P(规律)/P(现象)
也就是看见现象去推导出现这个现象背后的规律，这样就可以引入概率了，出现的可能性大小的区别了。网上的例子，就是你的汽车现在在响警报，然后你觉得是被砸了？还是被小孩子踢了一下？求出它们的概率。

P(A)一般叫做先验概率，单纯地评估A事件的概率；P(A|B)称为后验概率，就是在B事件发生的前提下，再去评估A事件发生的概率；P(B|A)/P(B)叫做可能性函数，这个就是一个调整因子，使得预估概率更接近真实概率，我的理解是，这个因子表达了条件A的发生是否，对于B的影响。

贝叶斯公式就在描述，有多大把握能相信一件证据。在事情发生的所有情况中，对于其中一种的置信度。

一个本来就难以发生的事情，就算出现某个证据和他强烈相关，也要谨慎。证据很可能来自别的虽然不是很相关，但发生概率较高的事情。

就像一个人很文静，然后你判断他是农民的可能性大还是图书管理员的可能性大。

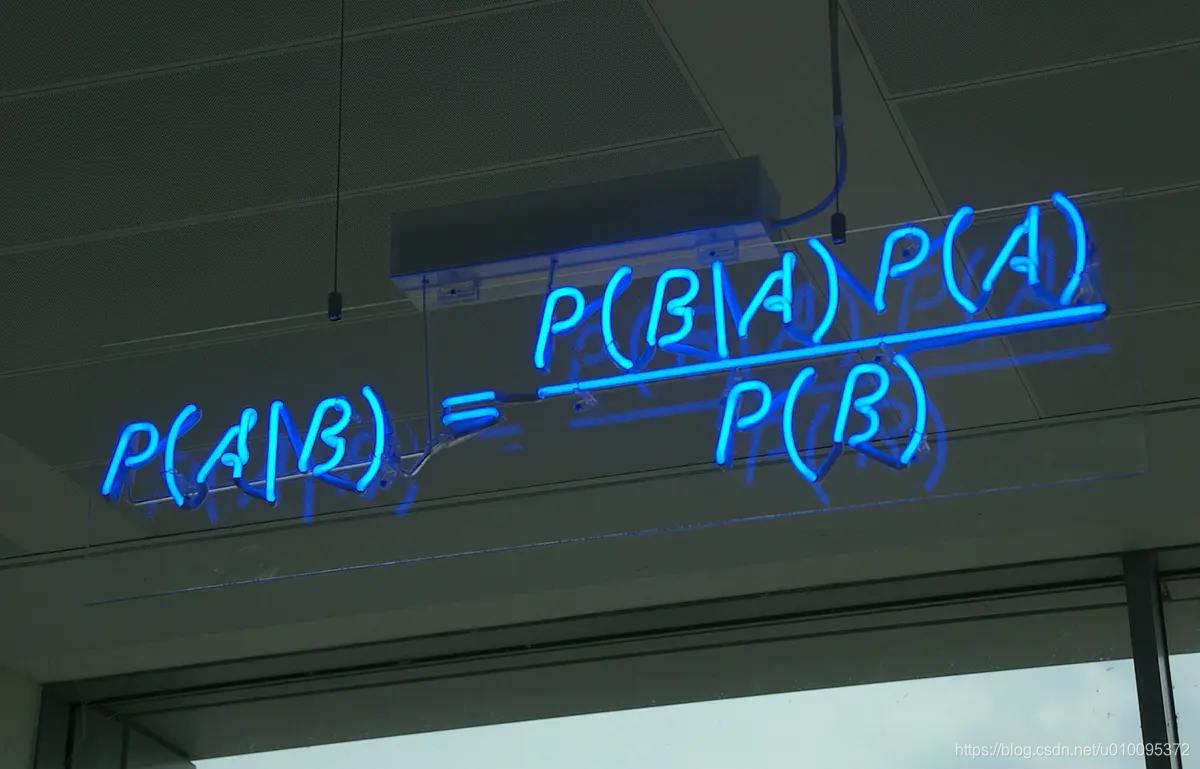
似然函数

似然函数和概率差不多一个意思，但是它们两个是从不同角度去描述。
P(x|θ)，这个概率有两个输入参数，x是变量，θ是模型的参数，emmm 这个就这么理解就好了，忽略参数有些怪异的。

如果θ是已知确定的，x是变量，这个函数叫做概率函数(probabilityfunction)，它描述对于不同的样本点x，其出现概率是多少。

如果x是已知确定的，θ是变量，这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数，出现x这个样本点的概率是多少。

就是说我知道了现象，然后倒推出那个最有可能的规律。

最大似然估计(MLE)

还是前面博客的例子，就是一个硬币，看看其是否均匀，抛十次，然后7次向上，3次向下，设定正面出现的概率是θ，这个实验的似然函数就写成，其中$x_0$表示这次实验结果。
$f(x_0,\theta )=(1-\theta )\times \theta \times \theta \times \theta \times \theta \times (1-\theta )\times \theta \times \theta \times \theta \times (1-\theta )={\theta }^7(1-\theta {)}^3=f(\theta )$
函数有了，就看看θ取什么值的时候f(θ)最大。

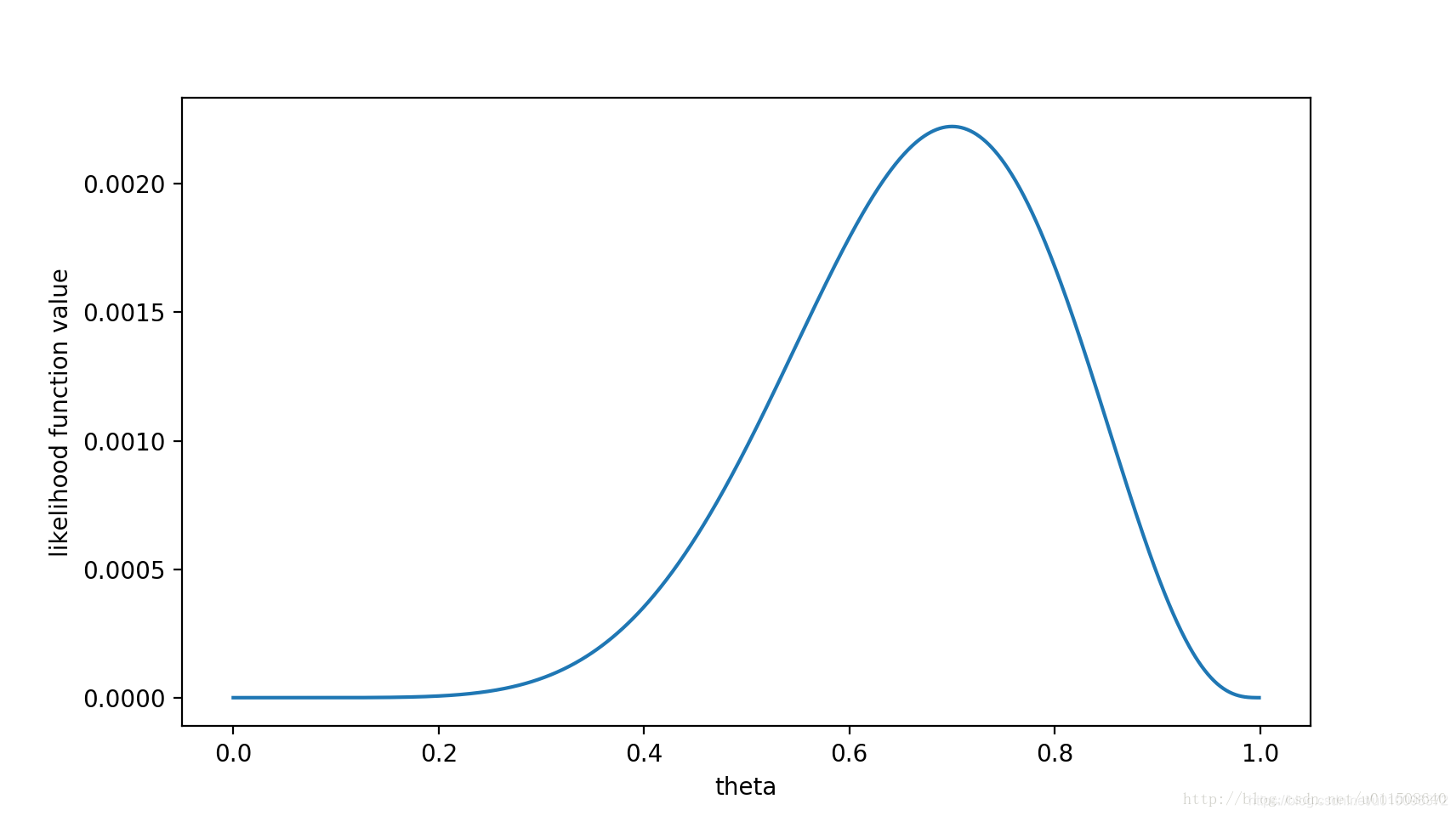
在θ等于0.7的时候最大，那么对于$x_0$这个实验θ=0.7，最让人信服。既然事情已经发生了，为什么不让其发生的概率最大呢？

最大后验概率估计(MAP)

最大后验估计是根据经验数据获得对难以观察的量的点估计。与最大似然估计类似，但是最大的不同时，最大后验估计的融入了要估计量的先验分布在其中。故最大后验估计可以看做规则化的最大似然估计。

最大似然估计求参数θ，并且将其看作固定的值，但最大后验概率估计是将其看作一个随机的值，有着某种的概率分布P(θ)，先验分布，这个先验分布就要我们自己估计经验判断，因此其认为使P(X|θ)P(θ)取最大值的θ就是最好的θ。那就是最大化$P(\theta |x_0)=P(x_0|\theta )P(\theta )/P(x_0)$，可以看出来$P(x_0)$是个固定值。我们可以计算。最大化$P(\theta |x_0)$就是最大化$P(x_0|\theta )P(\theta )$，而$P(\theta |x_0)$就是θ的后验概率。

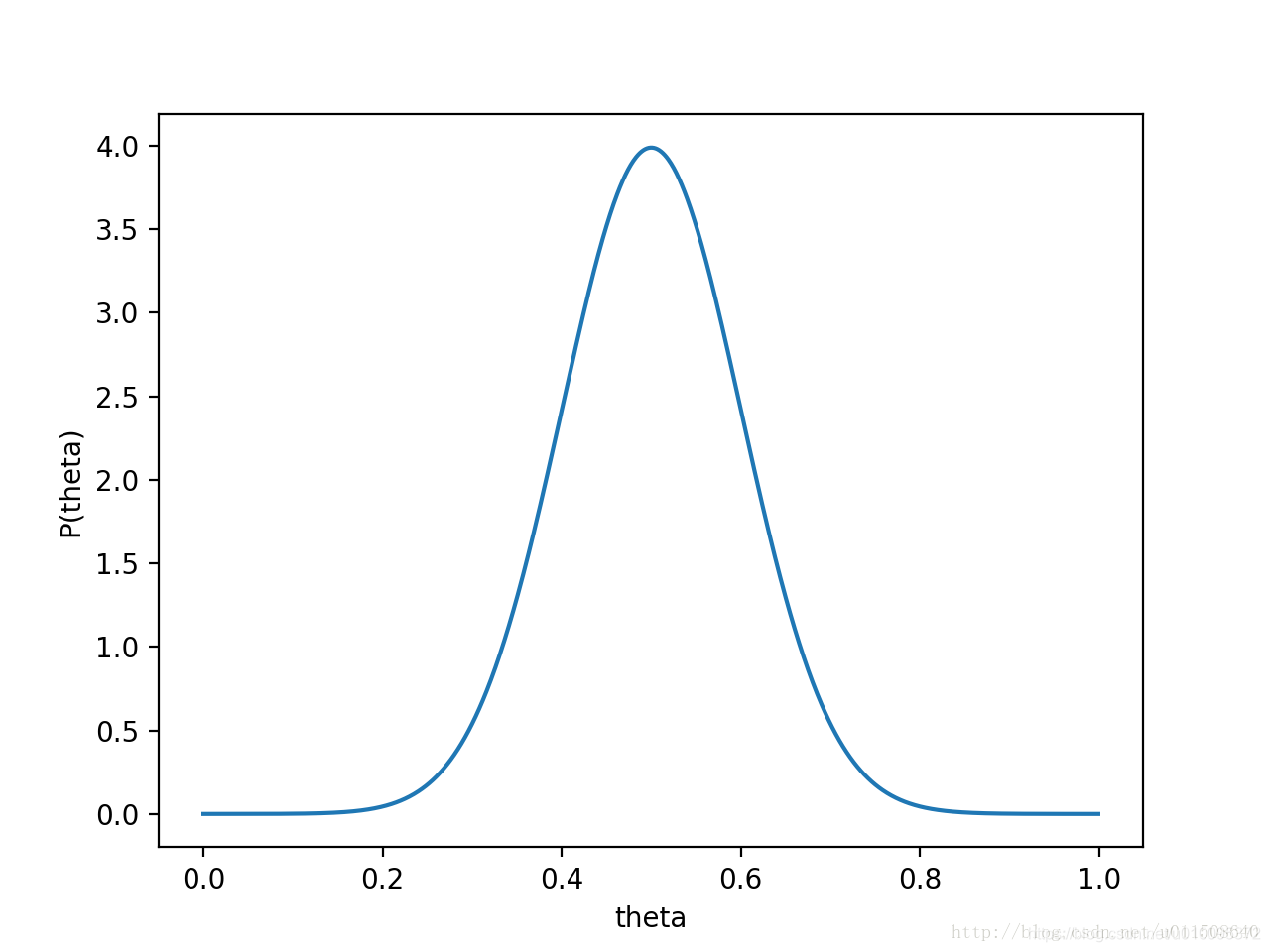
既然有两个参数一个$P(\theta )$一个是$P(x_0|\theta )$，要使他们两个的乘积变成最大，我们已经预估了一个$P(\theta )$，剩下就求$P(\theta )P(x_0|\theta )$的乘积好了，还是之前博客的例子。投硬币我们假定$\theta$为0.5，服从正态分布，$\theta$在0.5的可能最大，$P(\theta )$为均值0.5，方差0.1的高斯函数。

那$P(\theta )P(x_0|\theta )$的函数图像就是

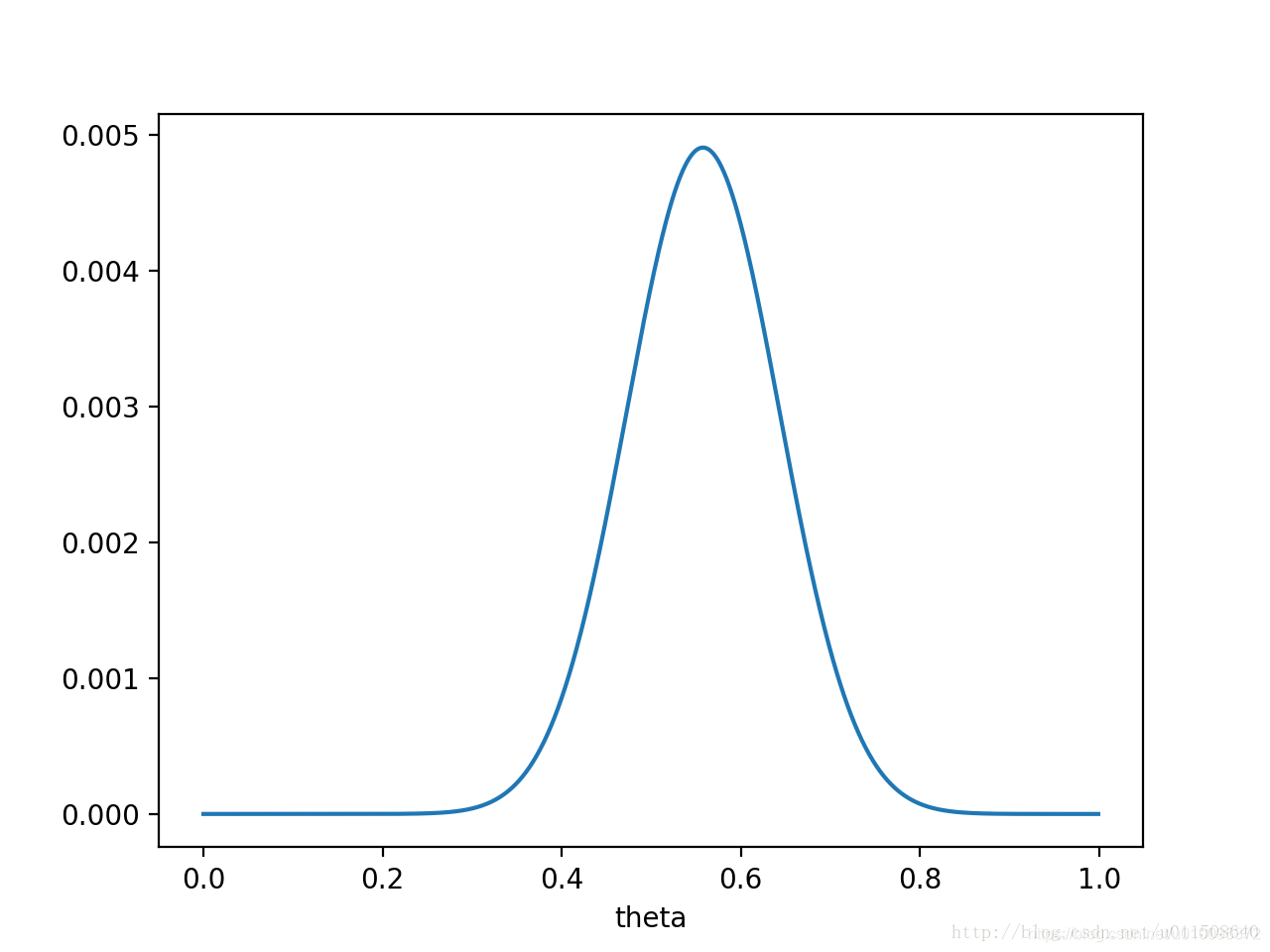
θ已经左移，不再是0.5了，而是θ=0.558，这个预估计的值也是蛮关键的。

贝叶斯估计

贝叶斯估计在MAP的基础上，不直接估值θ的值，但是贝叶斯估计不是直接估算某个值，而是估算θ的分布。$P(\theta |x)=P(x|\theta )P(\theta )/P(x)$，$P(x)$就是要求的全概率了。贝叶斯估计的数学描述：

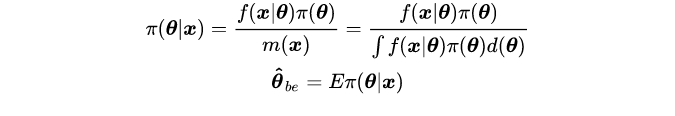
其中， $\Pi (\theta )$ 为参数 $\theta$的先验分布（prior distribution），表示对参数 $\theta$的主观认识，是非样本信息，$\Pi (\theta |x)$为参数 $\theta$ 的后验分布（posterior distribution）。因此，贝叶斯估计可以看作是，在假定 $\theta$服从$\Pi (\theta )$的先验分布前提下，根据样本信息去校正先验分布，得到后验分布 $\Pi (\theta |x)$。由于后验分布是一个条件分布，通常我们取后验分布的期望作为参数的估计值。

为了计算方便还引入了常见的共轭先验：Beta分布（二项分布）、Dirichlet分布（多项分布）。

Reference

贝叶斯公式由浅入深大讲解—AI基础算法入门
详解最大似然估计（MLE）、最大后验概率估计（MAP），以及贝叶斯公式的理解
从最大似然到EM算法浅解
极大似然估计和贝叶斯估计